【摘要】：回顾第3章的内容可以发现，与计算弹性力学平面问题时所采用的方法一样，二维温度场问题计算中所采用的三角形单元可以使用相同的形态函数，如图7-2所示。图7-2 三角形单元单元内的温度分布用结点上的温度值表示为如果某个单元完全处于物体内部，假定单元内的导热系数为常数，单元的面积为A，代入式单元的温度刚度矩阵为显然，单元的导热矩阵是对称的。
回顾第3章的内容可以发现，与计算弹性力学平面问题时所采用的方法一样，二维温度场问题计算中所采用的三角形单元可以使用相同的形态函数，如图7-2所示。
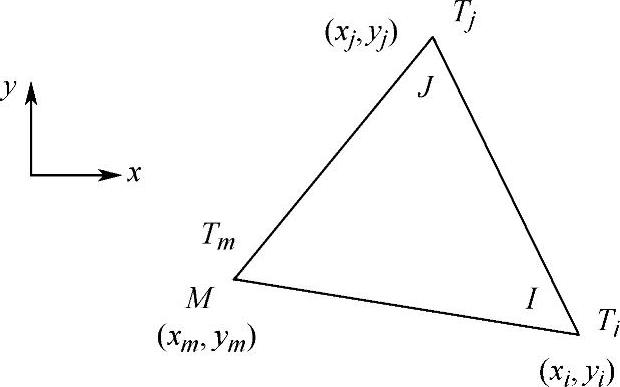
图7-2 三角形单元
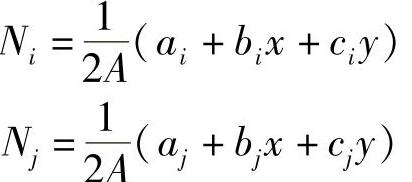
单元内的温度分布用结点上的温度值表示为
如果某个单元完全处于物体内部，假定单元内的导热系数为常数，单元的面积为A，代入式（7-24）
单元的温度刚度矩阵为
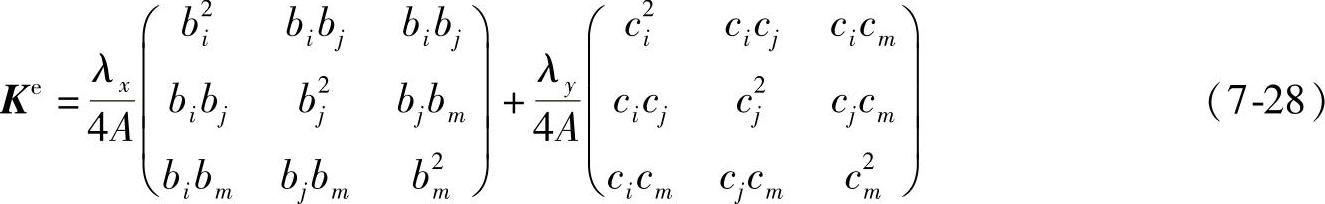
显然，单元的导热矩阵是对称的。
如果单元的内部热源为常数，由内部热源产生的温度载荷项为
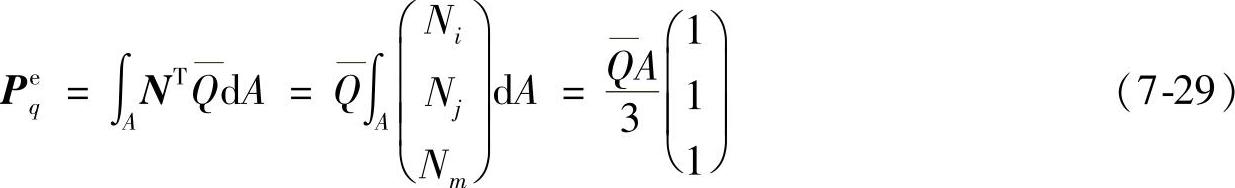
为方便起见，把换热边界统一表示为第三类换热边界，如果在单元边上存在换热边界条件，各条单元边上的边界换热条件将在单元温度刚度矩阵中生成附加项。单元边IJ所产生的附加项为，
(https://www.daowen.com)
在单元的IJ边上定义一个局部坐标s，与第2章的方法一样单元的形态函数用局部坐标表示为
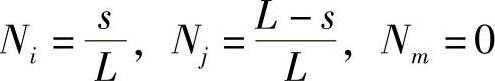
假定传热系数h为常数，
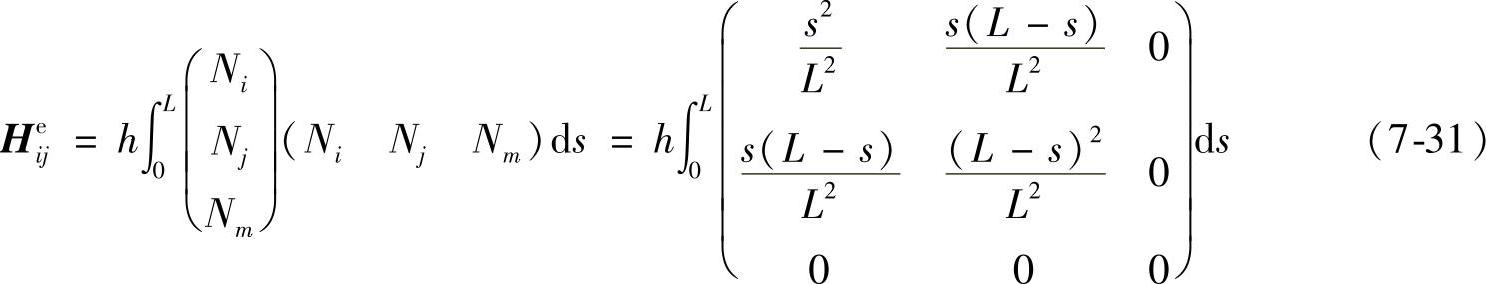
因此，在单元IJ边上存在换热边界条件所产生的附加项为，
同样，在单元JM、MI边上存在换热边界条件所产生的附加项为，
由边界换热条件生成的温度载荷向量为，
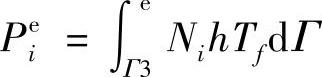
假定在单元的IJ边上传热系数与介质温度均为常数，由于IJ边上存在热交换而产生的温度载荷为
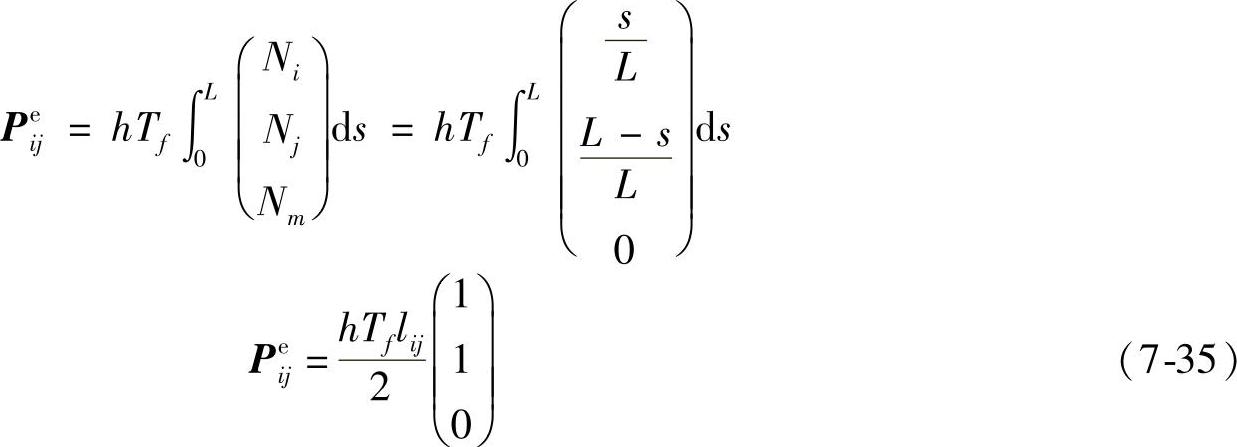
同样，在单元JM、MI边上存在换热边界条件所产生的温度载荷为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
