在前面已经介绍了有限元方法可以用来分析场问题，稳态温度场计算是一个典型的场问题。可以采用虚功方程建立弹性力学问题分析的有限元格式，推导出的单元刚度矩阵有明确的力学含义。在这里，介绍如何用加权余量法（Weighted Residual Method）建立稳态温度场分析的有限元列式。
微分方程的边值问题，可以一般地表示为未知函数u满足微分方程组，
未知函数u还满足边界条件，
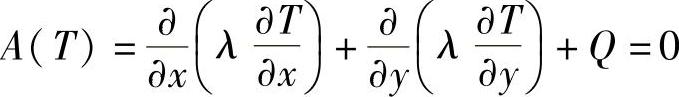
描述边界条件的方程如下，
B（T）=T-Ts=0（在第一类换热边界上）
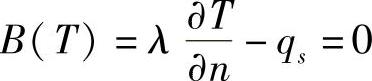（在第二类换热边界上）
上述微分方程组只有在区域的几何形状比较规则、边界条件比较简单时才能得到精确解，对于复杂几何形状的二维区域很难给出精确的解析解。
如果未知函数u是上述边值问题的精确解，则在域中的任一点上u都满足微分方程（7-10），在边界的任一点上都满足边界条件（7-11）。
对于复杂的工程问题，这样的精确解往往很难找到，需要设法寻找近似解。所选取的近似解是一族带有待定参数的已知函数，一般表示为，
式中，ai为待定系数；Ni为已知函数，被称为试探函数。
试探函数要取自完全的函数序列，是线性独立的。完全的函数序列是指任一函数都可以用这个序列来表示，例如完整的多项式序列、三角函数序列。采用这种形式的近似解不能精确地满足微分方程和边界条件，所产生的误差就称为余量。
微分方程（7-10）的余量为
R=A（Na） （7-13）
边界条件（7-11）的余量为
再选择一族已知的函数，使控制方程和边界条件余量的加权积分为零，即强迫近似解所产生的余量在某种平均意义上等于零，
式中，Wj和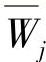
称为权函数，通过式（7-15）可以确定近似解中的待定参数ai。
这种采用使余量的加权积分为零来求得微分方程近似解的方法称为加权余量法。对权函数的不同选择就得到了不同的加权余量法，常用的方法包括配点法、子域法、最小二乘法、力矩法和伽辽金法（Galerkin method）。在很多情况下，采用Galerkin法得到的方程组的系数矩阵是对称的，在这里也采用Galerkin法建立稳态温度场分析的一般有限元列式。在Galer-kin法中，直接采用试探函数序列作为权函数，取Wj=Nj，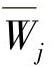
=-Nj。
下面用求解二阶常微分方程为例，说明Galerkin法（具体内容可参见王勖成编著《有限元法基本原理和数值方法》的1.2.3节）。
例7-1：求解二阶常微分方程
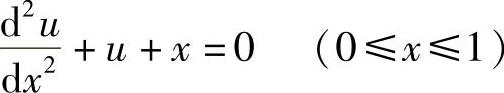
边界条件：当x=0时，u=0；当x=1时，u=0。取两项近似解，近似解满足边界条件：
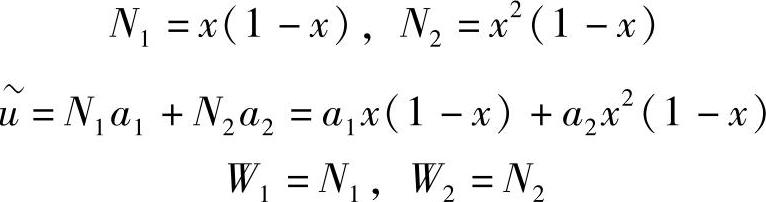
由式（7-15）可以得到两个加权积分方程，
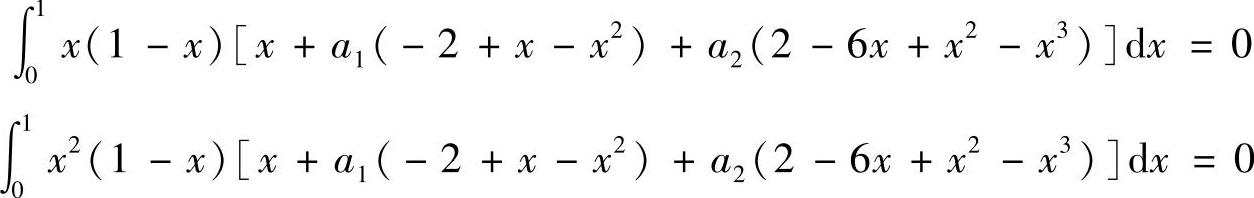
积分后可以得到一个二元一次方程组，解得，
a1=0.1924，a2=0.1707
近似解为(www.daowen.com)
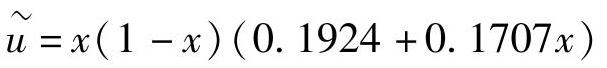
该方程的精确解为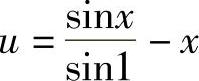
，近似解与精确解的结果比较如表7-1所示。
表7-1 近似解与精确解比较
例7-2：求解一维传热问题。假设材料的导热系数为1，微分方程为
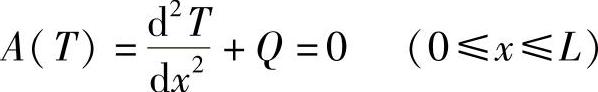
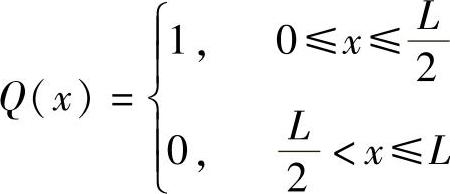
边界条件为，
T（0）=0，T（L）=0
分段求解二次场微分方程，
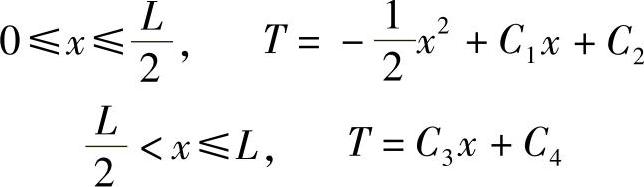
由边界条件T（0）=0，可得C2=0
由边界条件T（L）=0，可得C3L+C4=0
待求函数在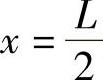
处连续，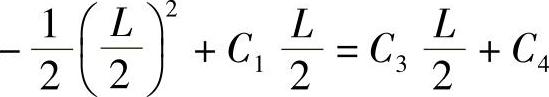
待求函数的一阶导数在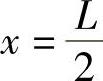
处连续，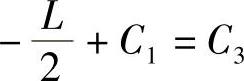
由边界条件解出所有待定系数，得到温度场分布的精确解答，
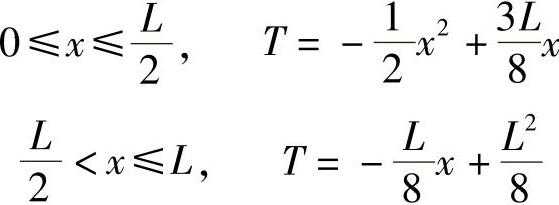
取傅里叶级数作为近似解，
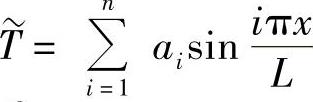
取两项近似解为，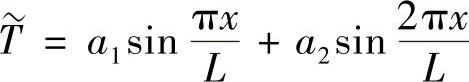
代入微分方程计算出余量，
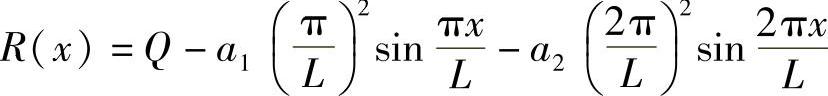
用配点法确定近似解的待定系数，配点位置为
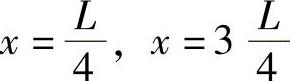
强迫在配点位置的余量为零，
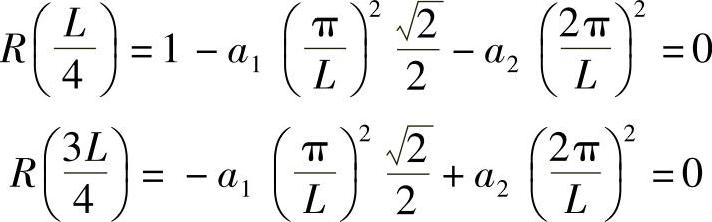
近似解中的系数为
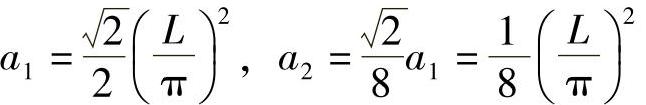
温度场分布的近似解答为
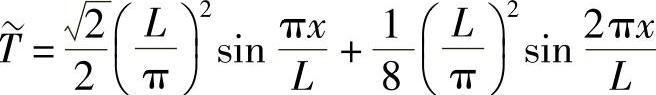
把精确解与近似解同时乘以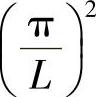
后画出曲线来对比。两个解答随x坐标变化的曲线在图7-1中给出，用菱形标记出的曲线是近似解，实线是精确解。相比较，两者在x小于0.2L部分很接近，在x大于0.2L部分存在比较大的偏差。
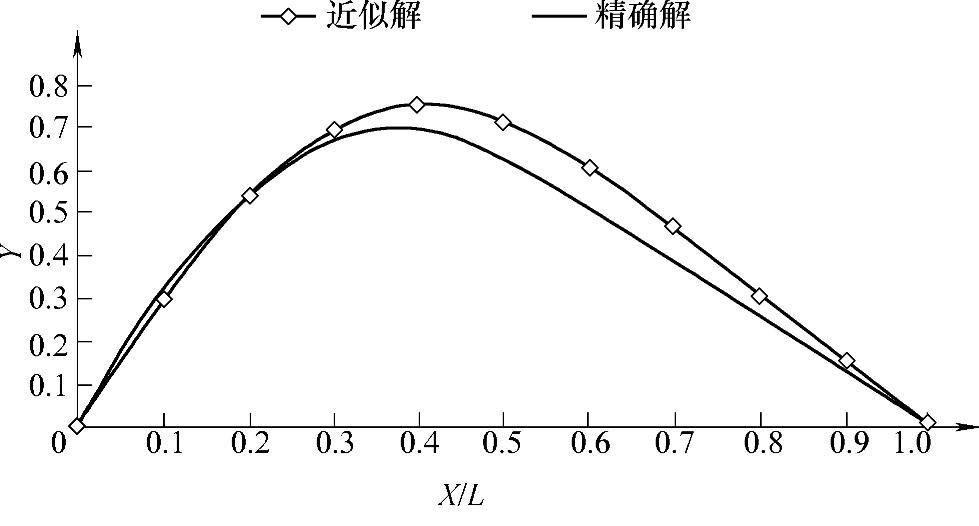
图7-1 精确解与近似解的对比
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
