传热过程是基本的物理过程之一，涉及许多工程应用领域，如铸造、热处理、焊接、高温锻造。在分析工程问题时，经常要了解介质或工件内部的温度分布情况，例如发动机的工作温度、金属工件在热加工过程中的温度变化、金属凝固过程的温度变化、流体温度分布等。物体内部的温度分布取决于物体内部的热量传递，以及物体与外部介质之间的热量交换，一般认为是与时间相关的。
法国数学家Jean Fourier在1822年提出了导热计算的基本规律：在物体内发生纯导热时，单位时间内通过垂直于热流方向的单位面积的热流量，与等温面法线方向上的温度增量成正比，而与法向距离成反比。
式中，λ为导热系数；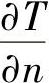
为温度梯度；式中的负号表示温度梯度的方向与热量传递的方向相反。
也可以写成矢量形式，
这个规律称为Fourier导热定律。
物体内部的热量传递采用以下的热传导方程（Fourier方程）来描述，
式中，ρ为密度（kg/m3）；c为比热容[J/（kg·K）]；λx，λy，λz为导热系数，[w/（m·K）]；T为温度（℃）；t为时间（s）；Q为内热源密度（w/m3）。
各向同性材料在不同方向上的导热系数相同，热传导方程可写为以下形式，
除了热传导方程，为了计算物体内部的温度分布，还需要指定初始条件和边界条件。初始条件是指物体最初的温度分布情况，
边界条件是指物体通过外表面与周围环境的热交换情况。在传热学中一般把边界条件分为以下三类。
1）给定物体边界上的温度，称为第一类边界条件。物体表面上的温度或温度函数为已知，(www.daowen.com)
T|s=Ts或T|s=Ts（x，y，z，t） （7-4）
2）给定物体边界上的热量输入或输出，称为第二类边界条件。已知物体表面上热流密度，
3）给定对流换热条件，称为第三类边界条件。物体与其相接触的流体介质之间的对流传热系数和介质的温度为已知
式中，h为传热系数[W/（m2·K）]；Ts是物体表面的温度；Tf是介质温度。
如果物质边界上的换热条件不随时间变化，物体内部的热源也不随时间变化，在经过一段时间的热交换后，物体内各点温度也将不随时间变化，即
这类问题称为稳态（Steady state）热传导问题。稳态热传导问题并不是温度场不随时间的变化，而是指温度分布稳定后的状态，我们不关心物体内部的温度场如何从初始状态过渡到最后的稳定温度场。随时间变化的瞬态（Transient）热传导方程就退化为稳态热传导方程，三维问题的稳态热传导方程为
对于各向同性的材料，可以得到以下的方程，称为Poisson方程，
考虑物体不包含内热源的情况，各向同性材料中的温度场满足Laplace方程，
在分析稳态热传导问题时，不需要考虑物体的初始温度分布对最后的稳定温度场的影响，因此不必考虑温度场的初始条件，而只需考虑换热边界条件。计算稳态温度场实际上是求解偏微分方程的边值问题。
温度场是标量场，将物体离散成有限单元后，每个单元结点上只有一个温度未知数，比弹性力学问题要简单。进行温度场计算时，有限单元的形函数与弹性力学问题计算时的完全一致，单元内部的温度分布用单元的形函数，由单元结点上的温度来确定。由于实际工程问题中的换热边界条件比较复杂，在许多场合表示下也很难进行测量，如何定义正确的换热边界条件仍然是温度场计算的一个难点。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
