例6-1：如图6-7所示的厚壁圆筒，高度H=30cm，内半径R1=10cm，外半径R2=15cm。材料弹性模量E=210GPa，泊松比μ=0.3。圆筒内壁承受均布压力作用，压力p=1000N/cm²。求受到载荷作用后，圆筒内外半径的变化量。

如图6-7所示的圆筒，几何形状、外载荷与约束条件都是关于圆筒的中心轴对称，因此，可以把它作为轴对称问题来处理。再根据其几何形状关于水平方向对称的特点，可以选取通过中心轴的纵截面的四分之一作为计算模型，如图6-8所示。在建立几何模型时，长度单位取cm，相应地弹性模量转换为2.1×10⁷N/cm²。

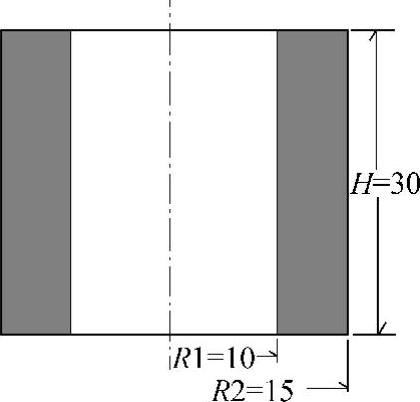
图6-7 厚壁圆筒

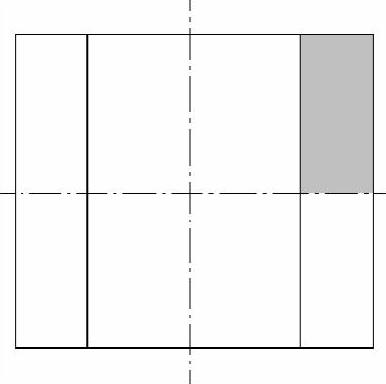
图6-8 厚壁圆筒的计算模型

1.选择单元类型，定义材料参数

可选42号单元，将单元行为设置为轴对称。选择Main menu＞Preprocessor＞Element type＞Add/Edit/Delete＞，选择单元后点击“Options”。在弹出的单元属性选择对话框中找到Element behavior（k3）右边的下拉复选框，选择Axisymmetric项，点击“OK”退出。

空心圆筒材料定义为各向同性的线弹性材料。

2.建立几何模型

创建一个矩形平面即可。在分析轴对称问题时，ANSYS总是把直角坐标系中y轴作为对称轴，因此几何模型的对称轴也必须是y轴。

3.划分有限元网格

沿半径方向设置4个单元边，沿高度方向设置10个单元边。采用四边形单元映射方式划分单元网格。

4.施加边界条件及载荷

1）在y=0的水平边界上施加y方向的位移边界条件uy=0。

2）在对应内壁的线段上加载均布的压力。

5.计算求解

在求解之前，切记执行Utility Menu＞Select＞Everything。

6.计算结果分析

1）显示圆筒沿半径方向的结点位移分布，如图6-9所示。(www.daowen.com)

2）给出内外半径的变化。沿内外壁分别定义两条路径，观察内外壁上的x方向位移沿高度的变化，如图6-10、图6-11所示。计算结果明显地与理论解存在一定的误差，内半径和外半径的变化按平均值计算。

从图6-10的结点位移分布可以明显地看出，采用Plane42单元的4×10网格不能达到预期的计算精度。

首先采用h方法提高计算精度。改进方案一：采用Plane42单元的8×10网格，结点位移分布、内表面上的径向位移分别如图6-12、图6-13所示。与最初方案相比没有明显改善。

图6-9 结点径向位移分布

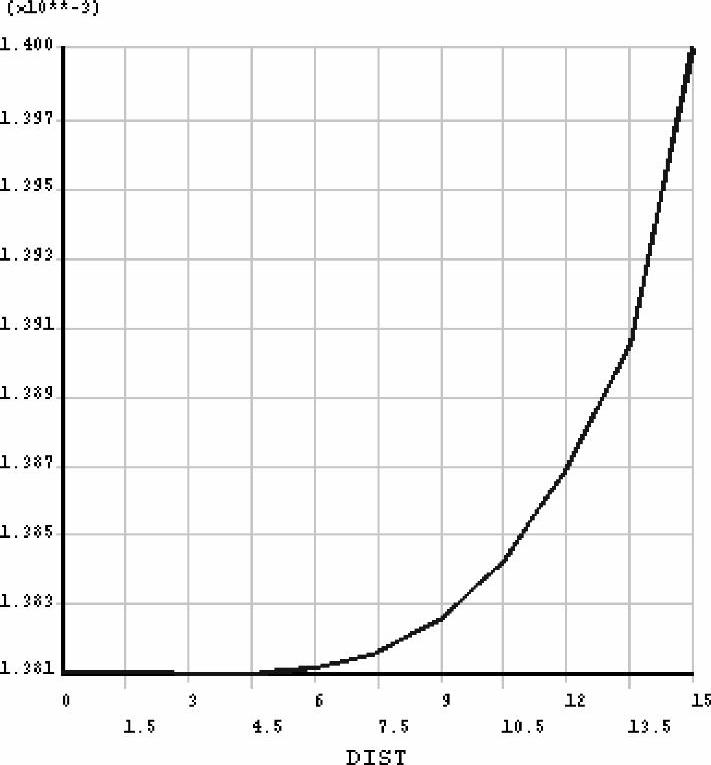
图6-10 内壁径向位移分布

图6-11 外壁径向位移分布

采用p方法提高计算精度。改进方案二：采用8结点Plane183单元的8×10网格，结点位移分布、内表面上的径向位移分别如图6-14、图6-15所示。方案二能够达到较好的计算精度。

图6-12 方案一结点位移

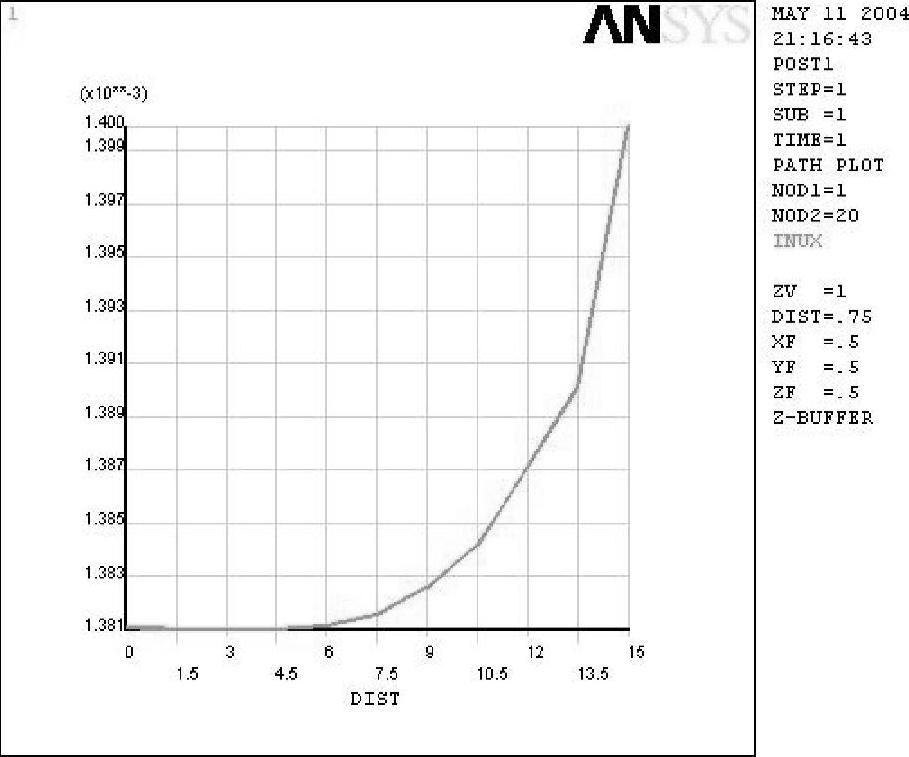
图6-13 方案一内壁位移分布

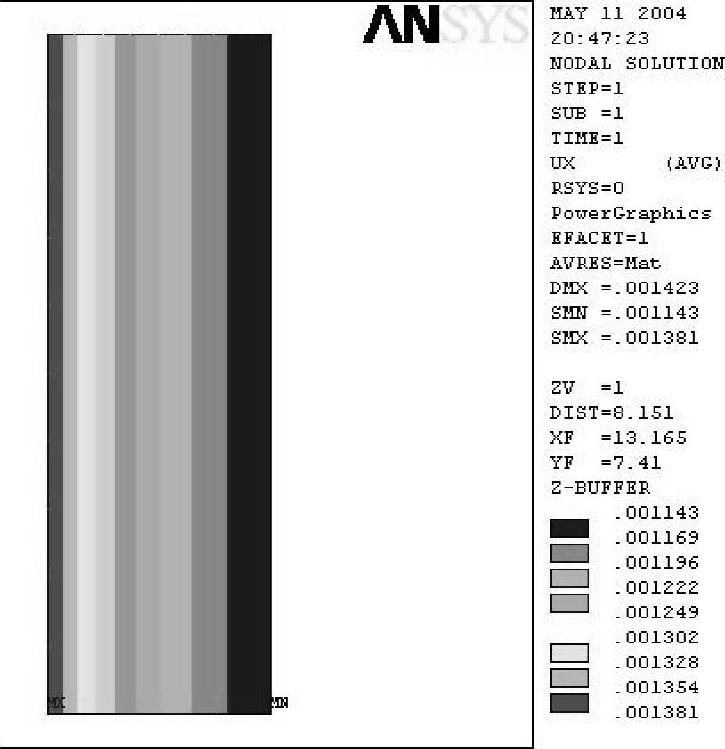
图6-14 方案二结点位移

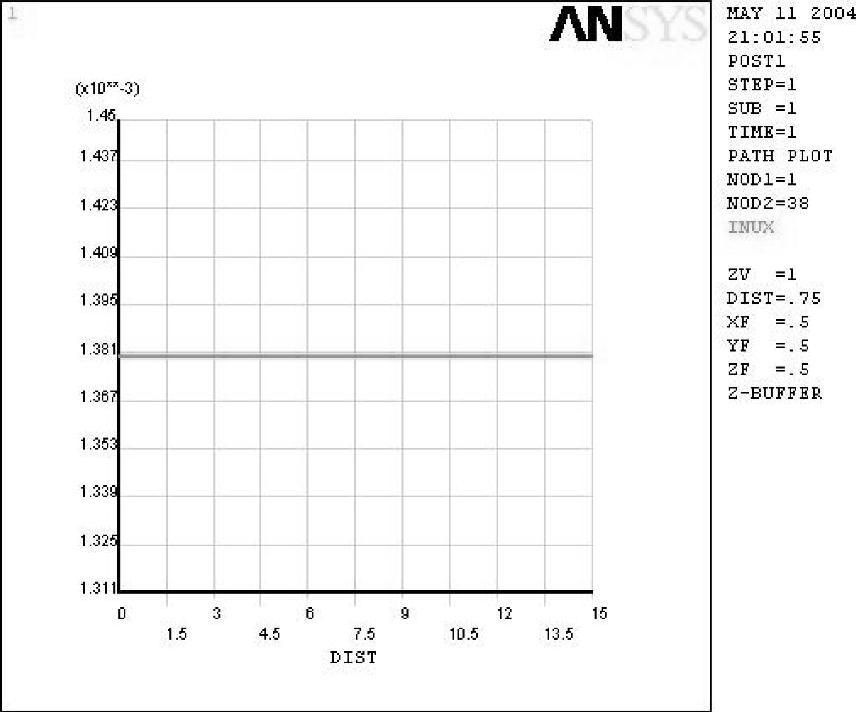
图6-15 方案二内壁位移分布