轴对称问题的几何方程

由式（6-20）式得，

其中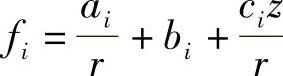，（下标轮换）

用几何矩阵表示单元的应变，

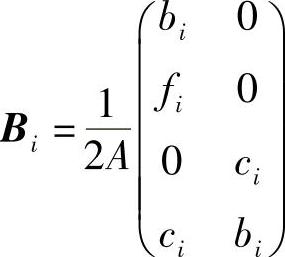（下标轮换） （6-24）

由于f_i是坐标r、z的函数，ε_θ分量在单元中不为常量，其他三个应变分量在单元中仍为常量。

广义胡克定律（Hooke’s Law）适用于正交坐标坐标系，由轴对称问题的物理方程，可得到弹性矩阵

令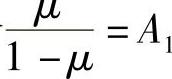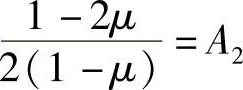，，则弹性矩阵为，

由弹性矩阵[D]和几何矩阵[B]可以得到应力矩阵[S]，并计算出单元内的应力分量，

S=DB （6-27）下标轮换，可得到S_j，S_m。(www.daowen.com)

由应力矩阵可知，除剪应力τ_zr为常量，其他三个正应力分量都是坐标r、z的函数。

单元刚度矩阵为，

单元刚度矩阵的分块矩阵为，

由于几何矩阵中的元素不是常量，单元刚度矩阵需要通过积分得到。由于B矩阵中包括项，上述积分运算较为复杂。特别当有单元边与对称轴重合时，出现r=0，这个积分就包括奇异项。为简化计算，通常用三角形单元形心位置的坐标r_c，z_c代替B矩阵中的变量r、z，即：

实际应用表明，只要网格剖分不太稀疏，采用这样的近似计算所引起的误差是很小的。把应变矩阵写成分块矩阵，

单元刚度矩阵的近似表达式为：

单元刚度矩阵的分块矩阵近似表达式为

与平面问题三结点三角形单元相比，轴对称问题三结点三角形单元的刚度矩阵推导过程基本相似，主要区别在于轴对称问题多出一个切向的应力分量，单元刚度矩阵不再是常数矩阵。形成整体刚度矩阵的步骤、位移约束的处理方法与第3章介绍的方法相似，在这里不再重复介绍。