如果物体的几何形状、约束情况及所受的外力都对称于空间的某一根轴，因此在物体中通过该轴的任何平面都是对称面，所有应力、应变和位移也对称于该轴，这类问题称为轴对称问题。研究轴对称问题时通常采用圆柱坐标系（r，θ，z），以z轴为对称轴。如图6-1所示的受均布内压作用的长圆筒，通过z轴的任意一个纵截面都是对称面。图6-2、图6-3所示的受力状态也是轴对称问题，因为通过z轴的任意一个纵截面都是对称面。

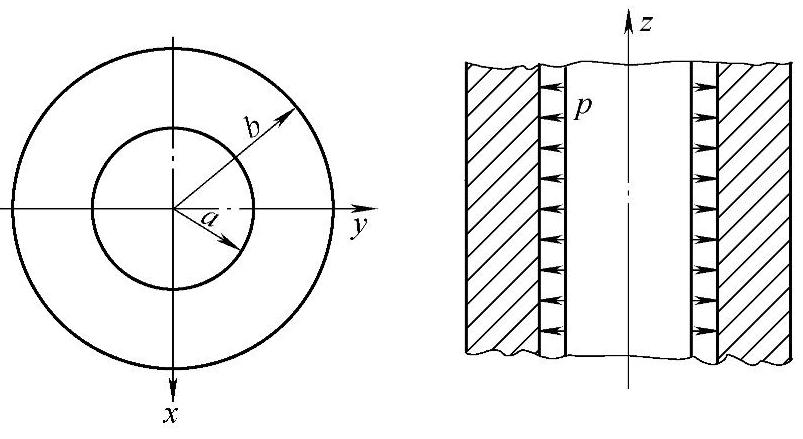
图6-1 受均布内压作用的长圆筒

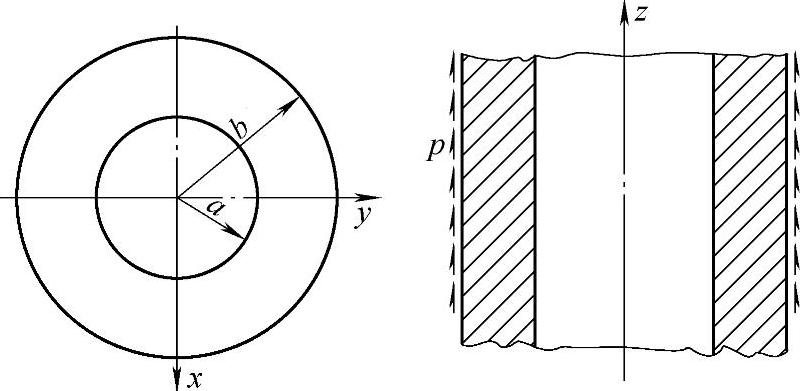
图6-2 外表面受均布面力作用的长圆筒

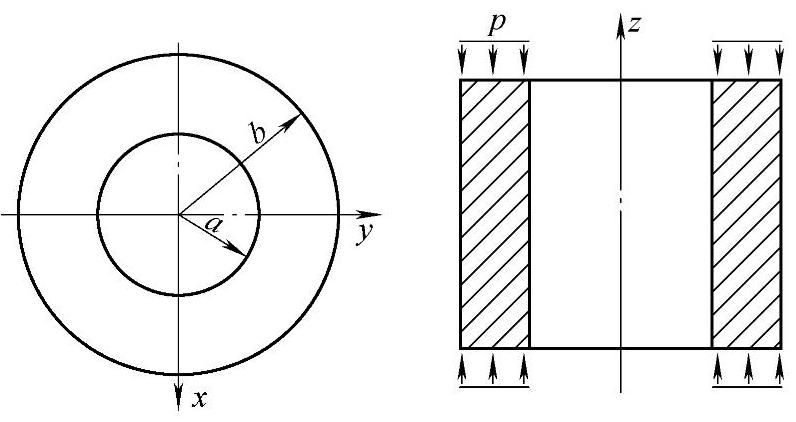
图6-3 两个端面受到均布压力作用的短圆筒

研究轴对称问题时，通常选择由相距dr的两个圆柱面，相距dz的两个水平面，夹角为dθ的两个垂直面分割成的六面体来研究，如图6-4a所示，图6-4b为单元体的横截面，图6-4c为单元体的纵截面。由于对称性，垂直于对称面的两个剪应力分量τ_rθ，τ_zθ不存在。如果存在τ_rθ、τ_zθ这两个剪应力分量，将破坏轴对称问题的对称性。轴对称问题共有4个应力分量：

式中，σ_r表示沿半径方向的正应力，称为径向应力；σ_θ表示沿θ方向的正应力，称为环向应力或切向应力；σ_z表示沿z方向的正应力，称为轴向应力；τ_zr表示在圆柱面上沿z方向作用的剪应力。

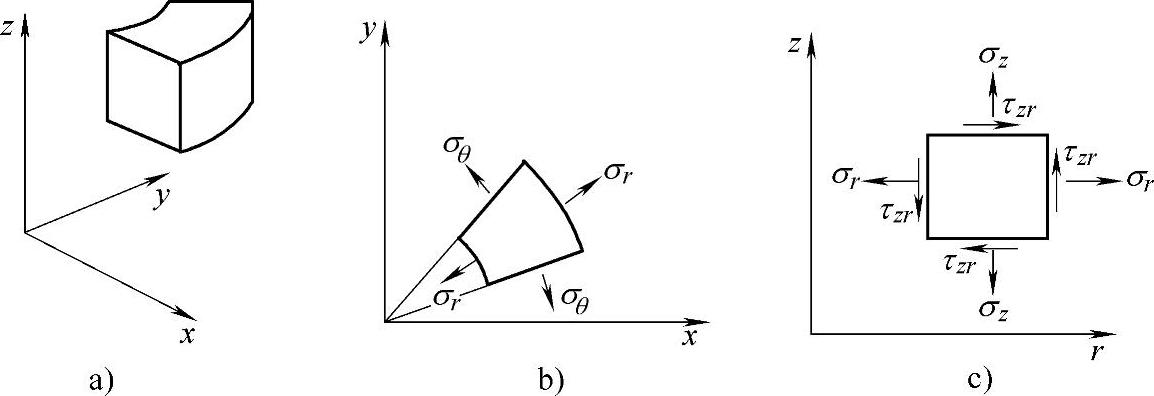
图6-4圆柱坐标系中的单元体

同样，轴对称问题共有4个应变分量：

式中，ε_r表示沿半径方向的正应变，称为径向正应变；ε_θ表示沿θ方向的正应变，称为环向正应变或切向正应变；ε_z表示沿z方向的正应变，称为轴向正应变；γ_zr表示沿r和z方向的剪应变。

在轴对称问题中，弹性体内任意一点上，不存在切向位移，只存在径向位移u和轴向位移w，两个位移分量表示为，

在前面章节讨论弹性力学平面问题的有限元法时，先由将弹性体划分为有限个单元的组合体，由虚功方程得到单元刚度矩阵，集成后得到整体刚度矩阵。在这里，用虚功方程直接得到轴对称问题的有限元列式。

由虚功方程可得，外力虚功等于内力虚功或虚应变能，

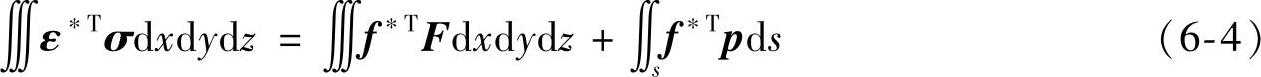
式中，F为真实的体力；p为真实的面力；f^*为虚位移；ε^*为对应于虚位移的虚应变。

将弹性体离散后，作用在弹性体上的外载荷移置到结点上，在每个结点上外力只有径向分量U₁，U₂，…，U_n，轴向分量W₁，W₂，…，W_n，写成向量形式如式（6-5）所示。

F=〔U₁W₁U₂W₂…U_nW_n〕^T （6-5）(www.daowen.com)

每个结点的虚位移也只有径向分量u₁^*，u₂^*，…，u_n^*，轴向位移分量w₁^*，w₂^*，…，w_n^*，写成向量形式如式（6-6）所示。

δ^*=（u₁^*w₁^*u₂^*w₂^*…u_n^*w_n^*）^T （6-6）

在单元中由虚位移引起的虚应变为

ε^*e=Bδ^*e （6-7）

单元中的实际应力为

σ^e=DBδ^e （6-8）

采用一些圆环单元将轴对称体离散，这些单元与对称面rz正交的截面形式各不相同，图6-5为三结点三角形环状单元。

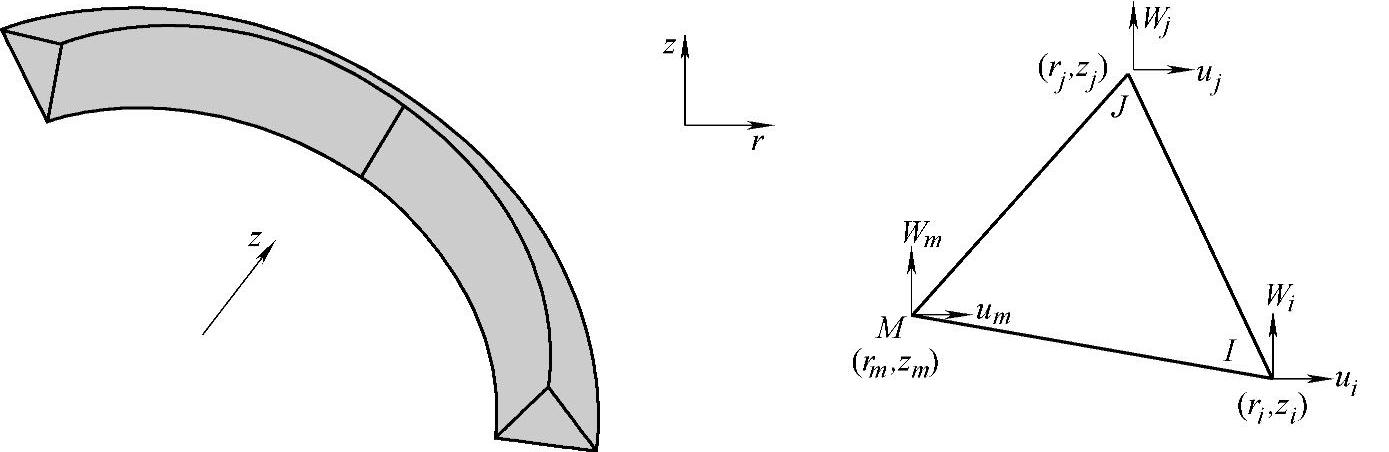
图6-5 三结点三角形环状单元

离散后的单元组合体的虚功方程为，

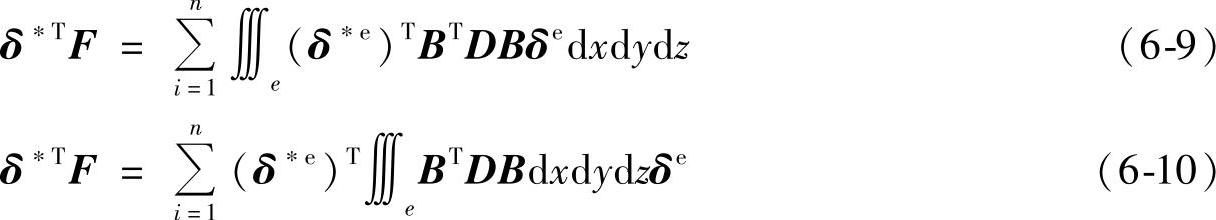
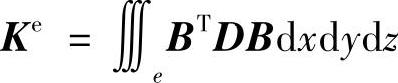为单元刚度矩阵。

对于轴对称问题，在圆柱坐标系中，所有物理量与圆周角度无关，可以得到以下的多重积分，

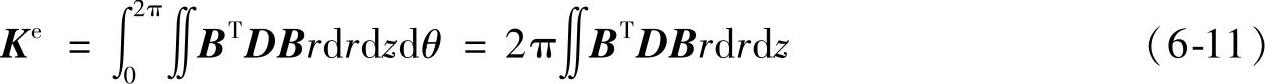
单元结点位移向量与整体结点位移向量之间的关系定义如下：

δ^*e=T^e{δ^*}，其中T^e为转换矩阵。

将式（6-11）和用整体结点位移表示的单元结点位移代入式（6-10）可得

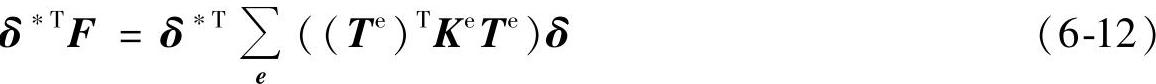
定义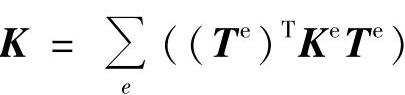为整体刚度矩阵，得到方程组

Kδ=F （6-13）

根据位移约束条件修改整体刚度矩阵之后，可以由式（6-13）解出全部的未知结点位移分量。