多数弹性力学问题需要按照三维空间问题来求解。三维弹性力学问题的有限元法的基本步骤与平面问题的步骤一样，包括单元离散化、选择单元位移模式、单元分析、整体分析和方程求解。在分析三维问题时，所选择的单元主要为四面体单元和六面体单元。每个单元结点上定义有三个位移分量u、v、w。

三维问题有限元法有以下两个主要难点：

1）单元划分比较复杂。无法采用人工方法完成复杂三维实体的单元划分，需要有功能强大的单元划分程序，从CAD模型直接生成离散的单元网格。现在的有限元软件可以读入IGES、STL等格式的图形交换文件。六面体单元的计算精度比较高，但是对于复杂三维实体无法实现六面体单元的自动划分。采用四面体单元能够实现单元自动划分，但是四面体单元的计算精度比较低。

2）计算规模大。三维问题的单元数目大，结点自由度多，导致计算规模大，对计算机硬件的要求很高。为缩短计算时间，有许多问题需要采用巨型计算机，如CRAY或并行计算机。

常用的三维等参单元有六面体八结点等参单元和六面体二十结点等参单元。等参单元的位移模式和坐标变化式采用相同的形函数，

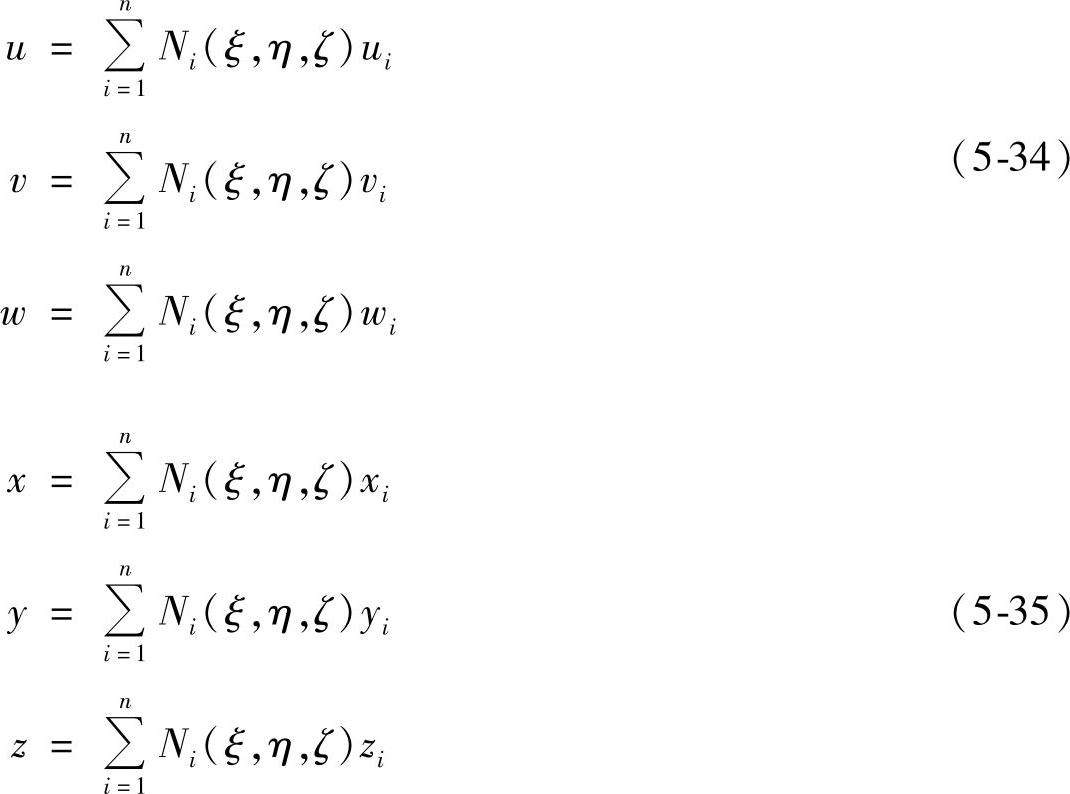
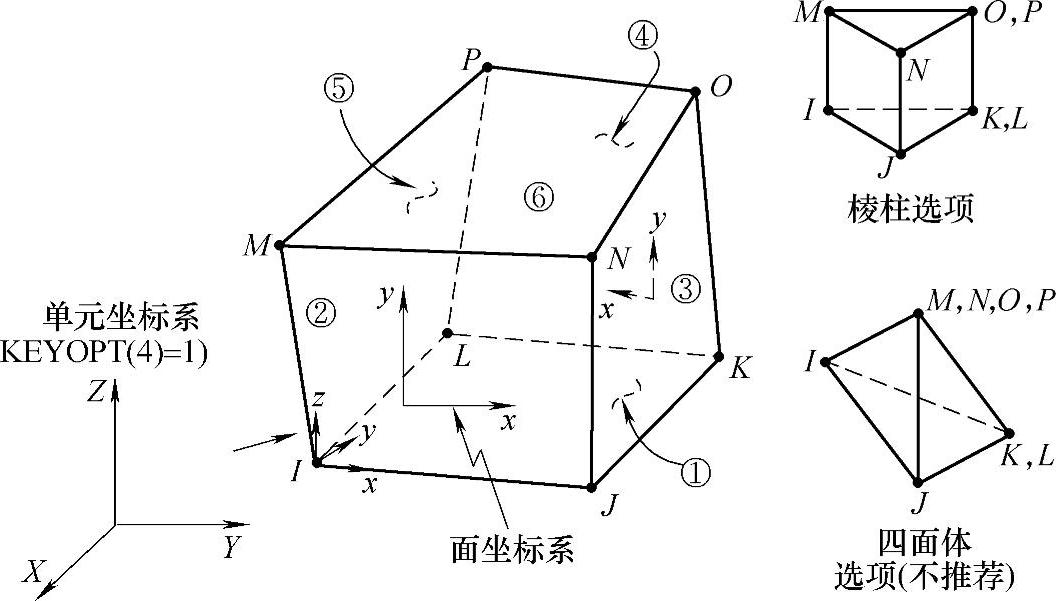
图5-12 ANSYS提供的Solid45单元

ANSYS提供的Solid45单元就是六面体八结点等参单元，每个结点有代表x、y、z三个方向位移的三个自由度（DOF，Degree of Freedom），可以退化为五面体棱柱和四面体单元，如图5-12所示。单元局部坐标为r，s，t，如图5-13所示，六面体八结点等参单元的基本单元如图5-14所示。

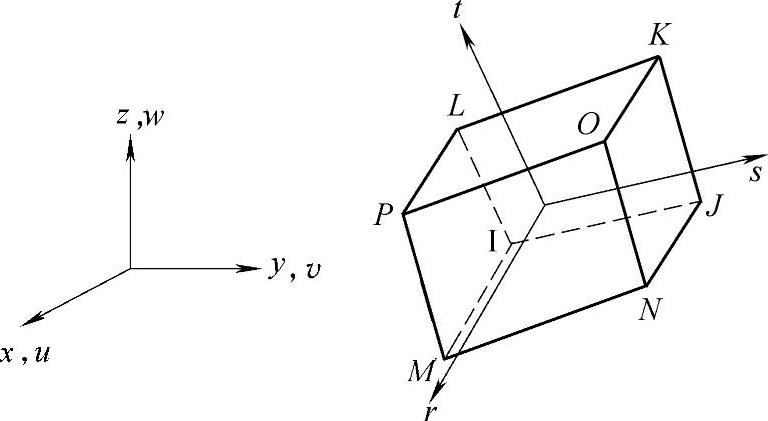
图5-13 Solid45的基本单元

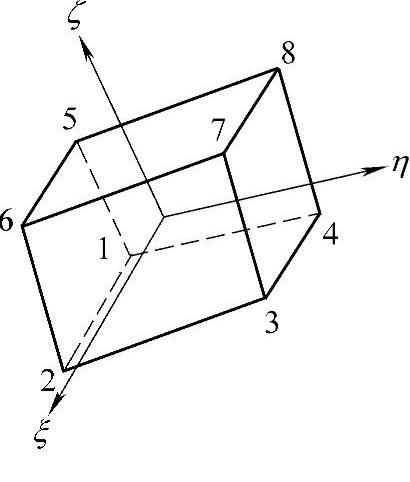
图5-14 八结点基本单元

六面体八结点等参单元的基本单元如图5-14所示，其形函数为，

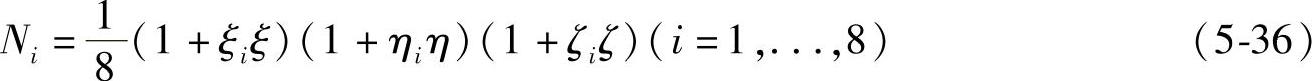
式中，ξ_i，η_i，ζ_i为结点的局部坐标。

如图5-15所示，ANSYS提供的Solid95单元是六面体二十结点等参单元，每个结点有代表x、y、z三个方向位移的三个自由度，可以退化为五面体棱柱、五面体金字塔形和四面体单元。Solid95单元的基本单元如图5-16所示。

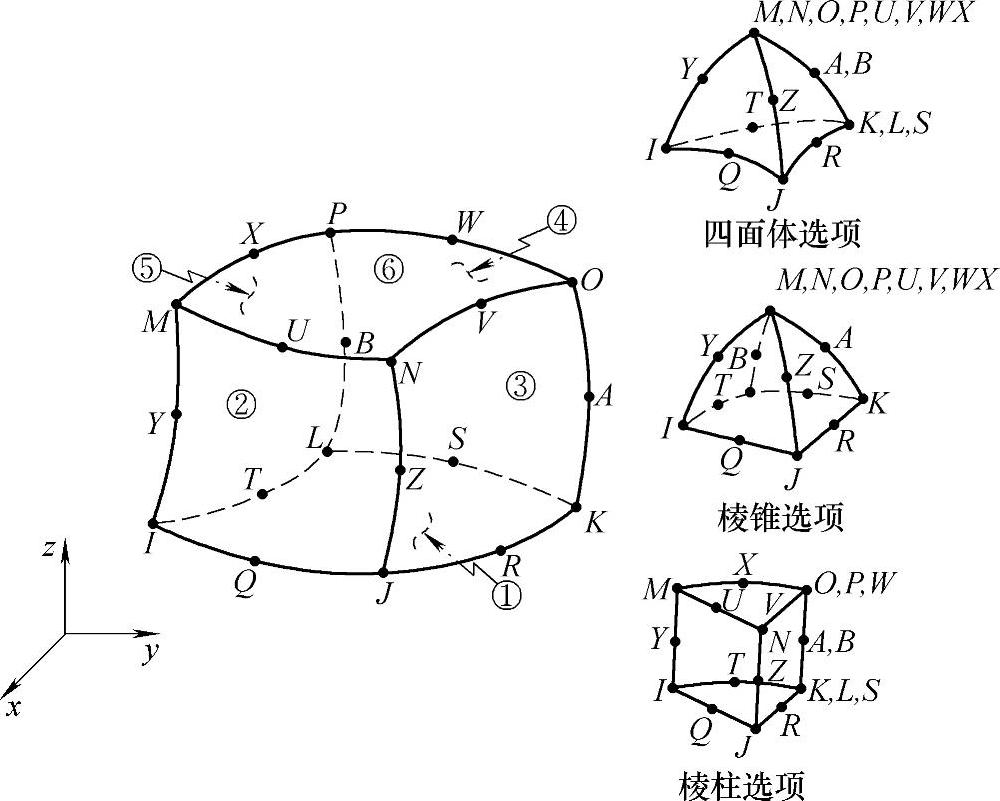
图5-15 ANSYS提供的Solid95单元

与六面体八结点等参单元相比，六面体二十结点等参单元能更好地适应不规则的形状，计算误差比较小，基本单元如图5-17所示，其形函数为，

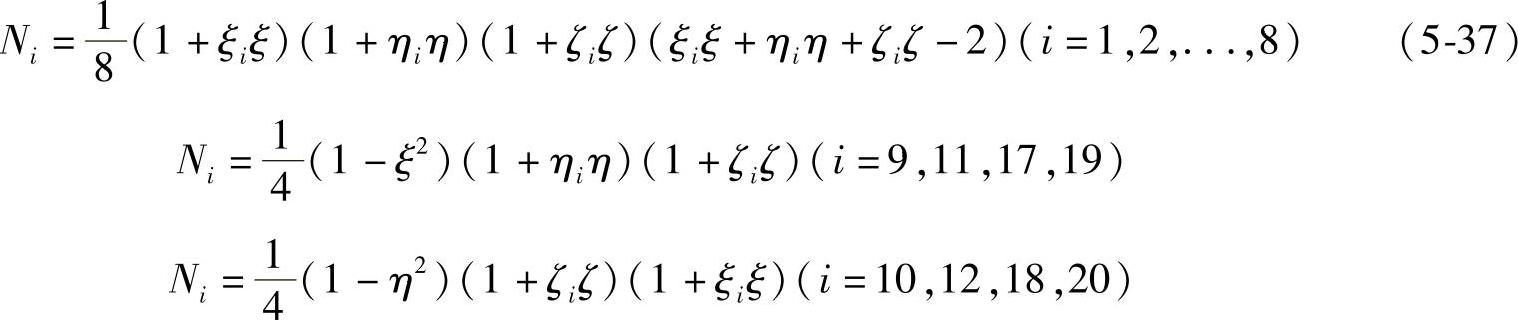
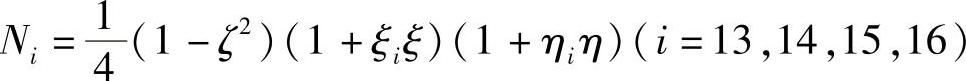
式中，ξ_i，η_i，ζ为单元结点在局部坐标系中的坐标。

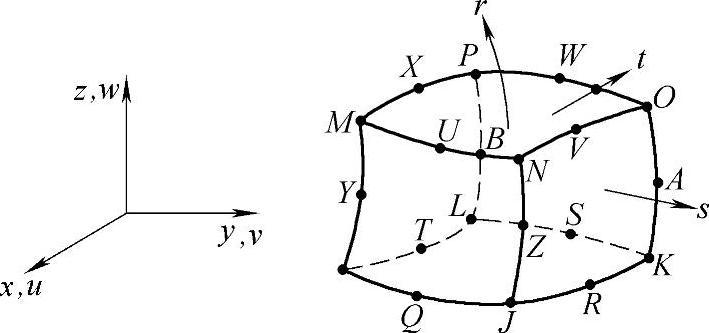
图5-16 Solid95的基本单元

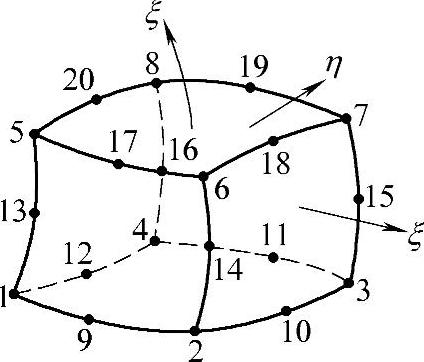
图5-17 二十结点基本单元(www.daowen.com)

单元刚度矩阵为

按照上节介绍的等参单元分析的基本步骤可以得到三维单元的单元刚度矩阵。

雅可比矩阵为

形函数对整体坐标的偏微分可以用雅可比矩阵表示为形函数对局部坐标的偏微分，

将式（5-35）代入式（5-39）可以计算出雅可比矩阵，

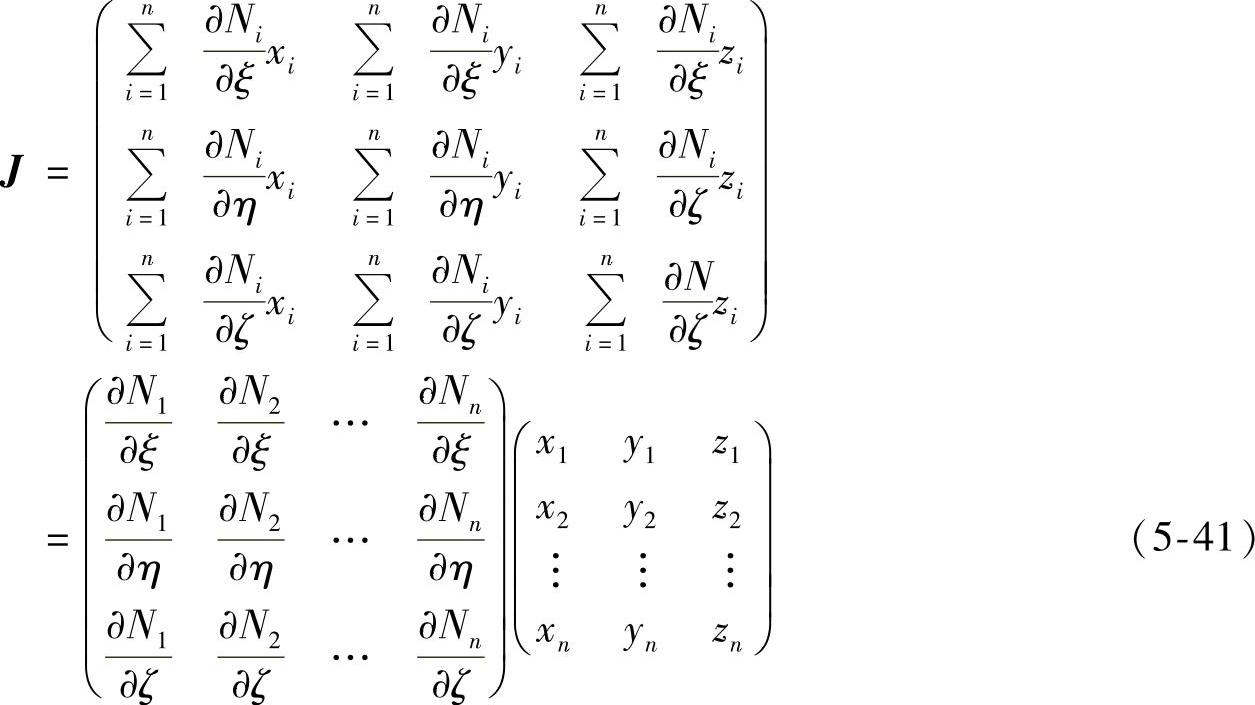
利用雅可比矩阵的行列式，将整体坐标系下的积分转换为在局部坐标系下的积分。

在整体坐标系中的体积微元为，

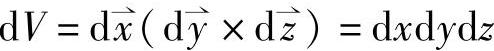
微矢量在局部坐标系中表示为，

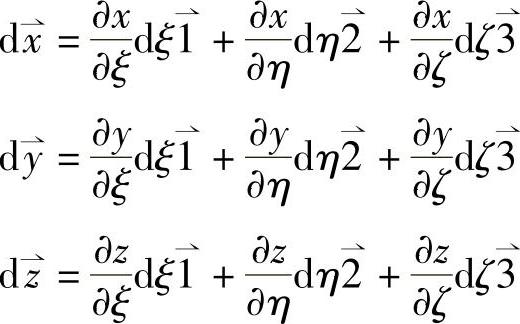
式中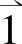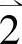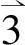，，，为局部坐标系中ξ，η，ζ方向上的单位向量。

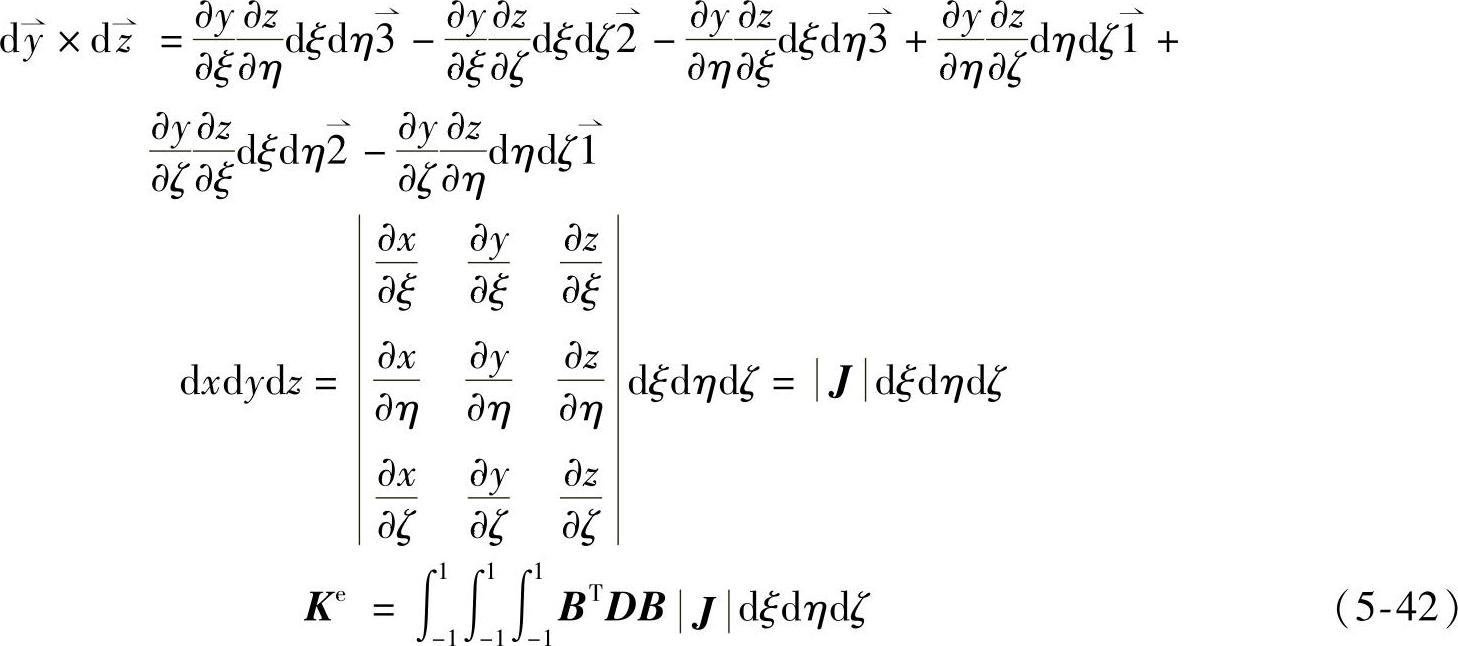
最后，用高斯积分计算出单元刚度矩阵。Solid45单元采用2×2×2积分方案，或采用单个积分点的减缩积分。Solid95单元采用14点积分方案，或采用2×2×2的减缩积分。

同样，用上节中类似的公式就可以在局部坐标下完成单元的载荷移置。当单元面为四边形时，Solid45单元采用2×2积分方案，Solid95单元采用3×3积分方案。

体力移置的公式为

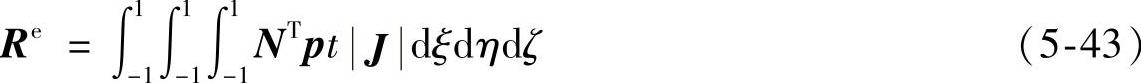
在ξ=1的面上受到面力作用，面力移置的公式为

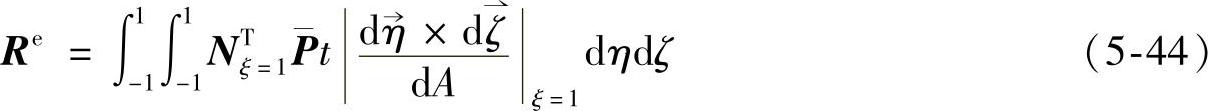
式中，dA=dηdζ，是基本单元边界上的微面积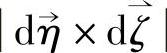；是实际单元边界上的微面积，是空间曲面，

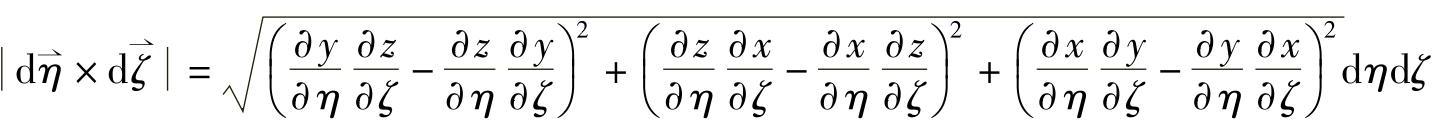
在点（ξ₀，η₀，ζ₀）集中力移置的公式为

R^e=N^T（ξ₀，η₀，ζ₀）P （5-45）