一维问题的高斯积分方法在[-1，1]的区间内预先定义了积分点的坐标和相应的加权系数，先求出被积分的函数在指定积分点上的数值，再加权后求和，就得到了该函数一维积分的结果。这种方法具有比较高的计算精度。一维问题的高斯积分公式可以很方便地推广到二维、三维问题。

一维高斯积分的定义如下，

式中，ξ_i为积分点位置；H_i为对应的加权系数。

对应于（-1，1）积分域，高斯积分中所采用的积分点坐标和对应的加权系数如表5-2所示。

表5-2 高斯积分的积分点坐标和加权系数

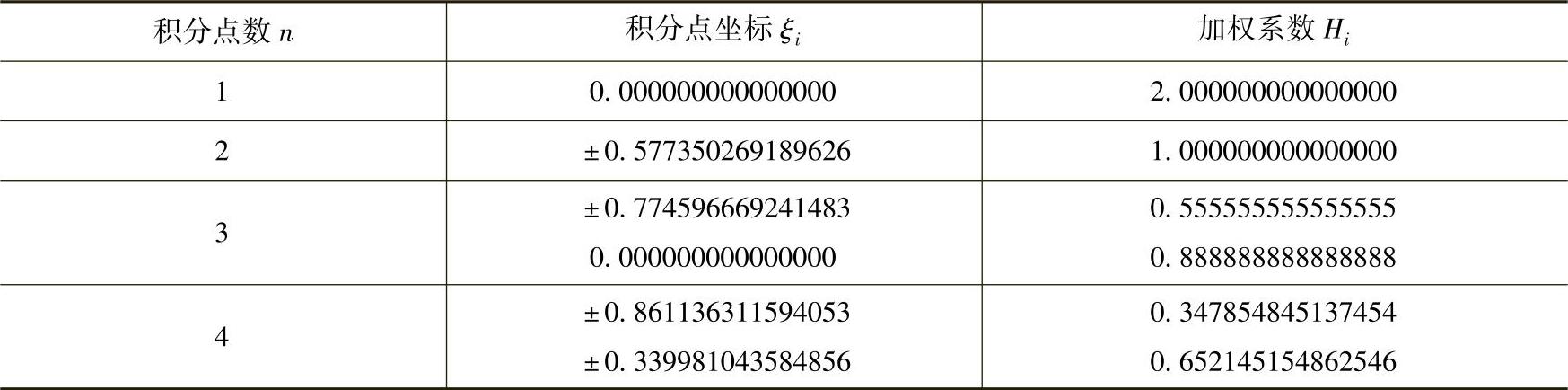
在任意积分域（a，b）上，用高斯积分公式计算时，先要把积分区域变换到（-1，1）区间上。二维、三维高斯积分可以用多重积分的方法，由一维高斯积分得到。

二维高斯积分，

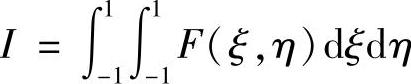
先令ξ为常数，按照一维高斯积分公式进行内层积分，

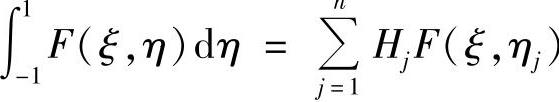
再用一维高斯积分公式进行外层积分，得到二维高斯积分公式，

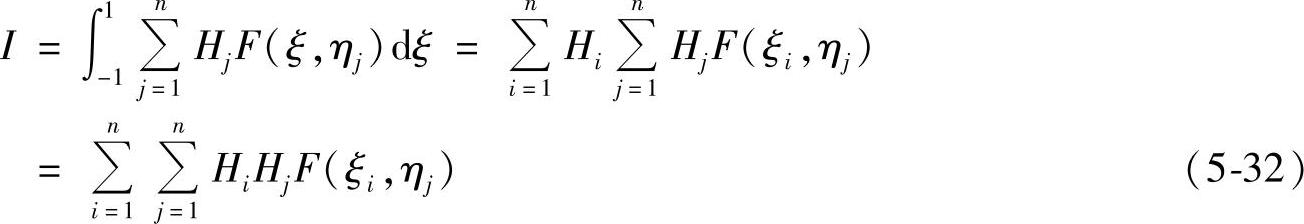
同样，进行三次分层积分，得到三维高斯积分公式

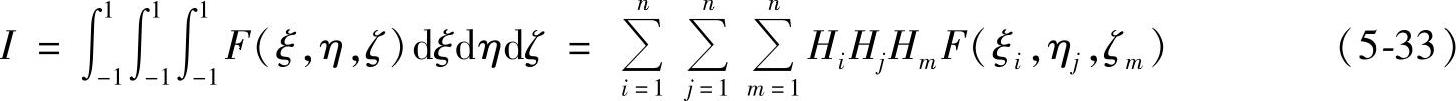
已经证明，采用n个积分点的高斯积分可以达到2n-1阶的精度，也就是说，如果被积分的函数是2n-1次多项式，用n个积分点的高斯积分可以得到精确的积分结果。下面通过计算两个简单多项式的积分，将高斯积分与精确积分结果做比较。

计算多项式的精确积分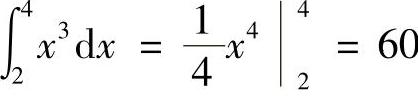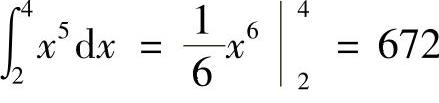：，。(www.daowen.com)

对三阶多项式用两个积分点进行高斯积分，

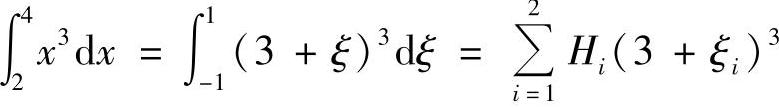
将表5-2中的积分点坐标和加权系数代入，积分点坐标与加权系数取5位有效数字，

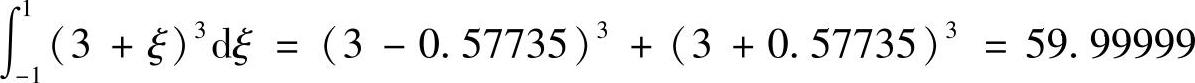
同样，对五阶多项式用两个积分点进行高斯积分，

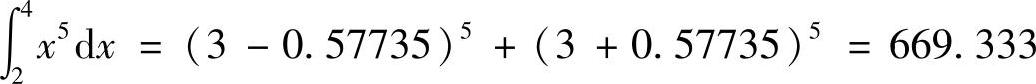
对五阶多项式用三个积分点进行高斯积分，积分点和加权系数均取5位有效数字

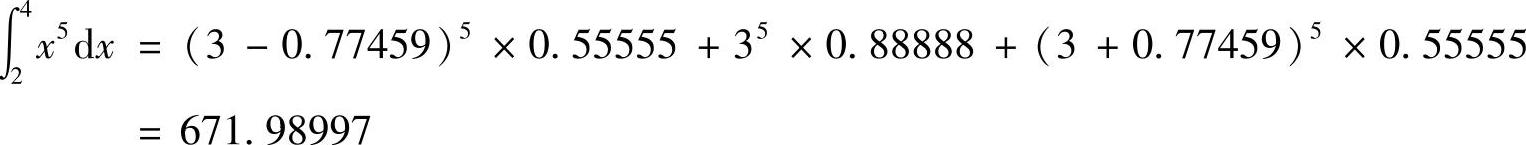
用这两个多项式的积分结果，可以验证n点高斯积分是2n-1阶精确积分的结论。同时，我们也发现高斯积分即使不是精确积分，仍有比较好的精度。关于高斯积分方法的更多内容参见，王勖成、邵敏编著的《有限元方法基本原理和数值方法》的4.5节数值积分方法。

那么，对于前面章节讲过的三角形单元，是否也能使用数值积分计算单元刚度矩阵的系数？在三角形单元中，自然坐标是面积坐标，计算单元刚度矩阵系数的积分具有以下的形式

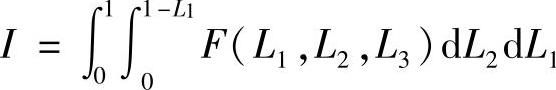
可以采用Hammer积分来计算。

除了高斯积分，常用的数值积分方法还有Newton-Cotes积分和Irons积分。

当计算中必须进行数值积分时，如何选择数值积分的阶次直接影响计算结果的精度和计算量。选择数值积分阶次的原则如下：

1）保证积分的精度。需要根据被积函数中的多项式阶次进行选择，尽量满足精确积分的条件。为了提高计算效率，可选取高斯积分的阶次低于被积函数精确积分所需要的阶次进行计算，这种积分方案被称为减缩积分。

2）保证结构总刚度矩阵K是非奇异的。这个条件讨论起来比较复杂，简单地可以概括为：全部积分点能提供的独立关系的数目要大于系统的独立自由度数。当采用减缩积分时，一定要使积分方案满足本条件。

四边形四结点、八结点的等参单元通常采用2×2的高斯积分，如ANSYS的PLANE42、PLANE82单元。