与三结点三角形单元相比，矩形单元的结点数目更多，形态函数的阶次也增加了，能够提高计算的精度。采用规则形状的矩形单元，在求解问题时，常会遇到不能适应边界形状的困难。另一方面，如果任意形状的四边形四结点单元采用矩形单元的位移模式，则在公共边界上不满足位移连续性条件。为了既能得到较高的计算精度，又能适应复杂的边界形状，可以采用坐标变换。

在如图5-3所示的任意四边形单元上，用等分四条边的两族直线分割四边形，以两族直线的中心为原点，建立局部坐标系（ξ，η），沿ξ及η增大的方向作为ξ轴和η轴，并令四条边上的ξ及η值分别为±1。为了求出位移模式，以及局部坐标与整体坐标之间的变换式，在局部坐标系中定义一个四结点正方形单元，如图5-4所示。参照矩形单元确定形态函数的过程，四结点正方形单元的位移模式为

u=N₁u₁+N₂u₂+N₃u₃+N₄u₄

v=N₁v₁+N₂v₂+N₃v₃+N₄v₄ （5-7）

式中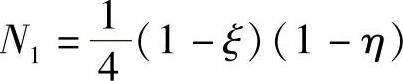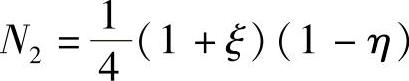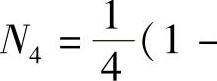，；；；ξ）（1+η）。

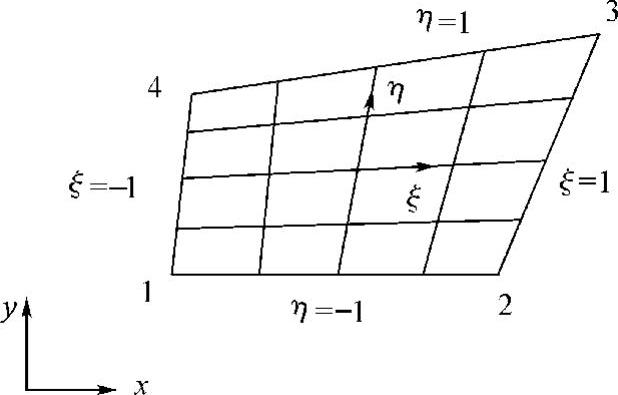
图5-3 任意四结点四边形单元

图5-4 四结点正方形单元

四个结点的坐标为（ξ_i，η_i），定义新的变量，

ξ₀=ξ_iξ，η₀=η_iη（i=1，2，3，4） （5-8）

形态函数表示为

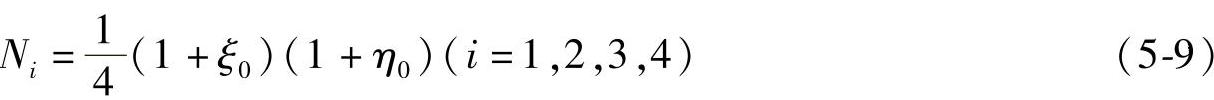
把ξ及η作为任意四边形单元的局部坐标，把式（5-7）的位移模式和式（5-9）的形态函数用于任意形状的四边单元，可得：

1）在四个结点处可以得到结点的位移。(www.daowen.com)

2）在单元的四条边上位移线性变化，保证了单元公共边界上位移的连续性。

因此，给出任意四边形单元的结点位移就能得到整个单元上的位移，式（4-7）的位移模式就是所要找的正确的位移模式。

为什么采用局部坐标进行变换后，就能保证在单元公共边界上的位移连续？因为在四边形单元的任意一条边上，局部坐标ξ、η中的一个会取为常数，单元边上的位移仅是局部坐标ξ、η中一个的线性函数，所以单元边上的位移可以由两个端点上的位移唯一确定。

把局部坐标与整体坐标的变换式也取为与位移模式相同的形式，

将坐标变换式用于任意四边形单元，可得：

1）在四个结点处给出结点的整体坐标。

2）在四条边上的整体坐标是线性变化的。

只要给出任意四边形单元四个结点的整体坐标，用式（5-10）就可以建立局部坐标系中的正方形单元和整体坐标系中的任意四边形单元之间的坐标变换关系。

把图5-4中在局部坐标系中的正方形单元称为基本单元。把图5-3中在整体坐标系中的任意四边形单元看作由基本单元通过坐标变换得来的，称为实际单元。

单元几何形状和单元内的未知量采用相同数目的结点参数以及相同的插值函数进行变换，称为等参变换。采用等参变换的单元，称为等参单元（Isoparametric element）。

由于形态函数N_i正好反映了单元形状的变化，也称为形函数（Shape function）。

采用等参单元，可以在局部坐标系中的规则单元上进行单元分析，然后在映射到实际单元上。等参单元同时具有计算精度高和适用性好的特点，是有限元程序中主要采用的单元形式。等参单元的提出是有限元法发展成为现代工程领域中广泛应用数值分析方法的极为重要的一步。