在前面的章节中研究了三结点三角形单元，如果研究的平面问题的几何形状是矩形，可以选择四结点的矩形单元，如图5-1所示，该矩形单元的边与坐标轴平行，在x及y方向的边长分别为2a和2b。

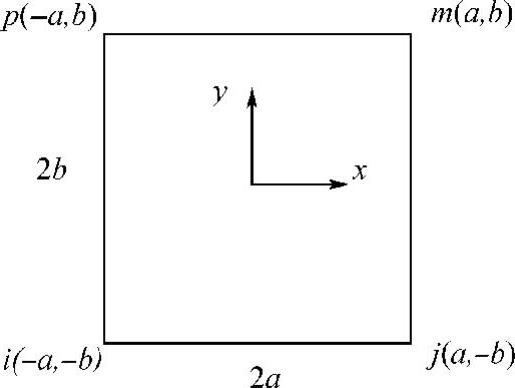
图5-1 四结点矩形单元

同第3章的方法类似，将单元的位移模式选为完全多项式序列的前4项，

u=a₁+a₂x+a₃y+a₄xy

v=a₅+a₆x+a₇y+a₈xy （5-1）

为了确定式（5-1）中的系数，可以将结点坐标与结点位移分量带入，然后进行矩阵求逆的运算，得到如式（5-2）所示用形态函数表示的单元位移。

u=N_iu_i+N_ju_j+N_mu_m+N_pu_p

v=N_iv_i+N_jv_j+N_mv_m+N_pv_p （5-2）

Ni就是插值函数，为避免进行矩阵求逆的运算和繁琐的推导，通常采用自然坐标的拉格朗日插值多项式直接构造形态函数。

对于包含n个结点的一维单元，结点参数是场函数的结点值，则单元内的场函数可以用插值函数表示为，

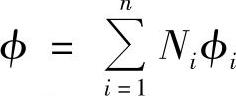
在i结点上，一维问题的拉格朗日插值多项式为

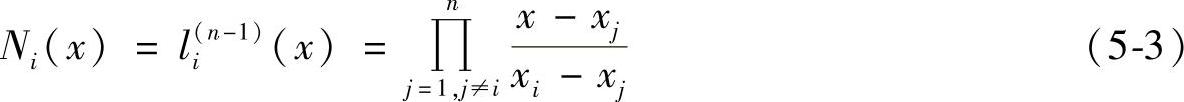
当n=2时，

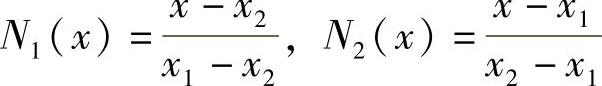
为方便构造单元插值函数，引入自然坐标，

式中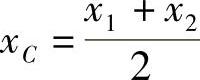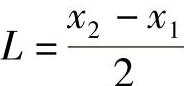，；，假定x₂＞x₁。式（5-3）表示为

当n=2时，ξ₁=-1，ξ₂=1，

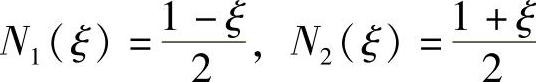(www.daowen.com)

对于图5-1所示的四结点矩形单元，引入自然坐标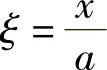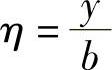，，，在自然坐标中的正方形如图5-2所示。

用两个方向上的插值多项式的乘积，可以构造出自然坐标中正方形单元的插值函数。

由式（5-5）可得在ξ轴方向上，

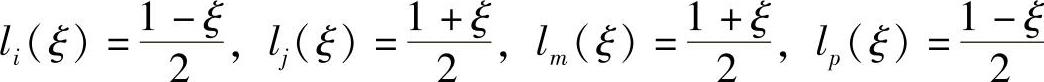
在η轴方向上

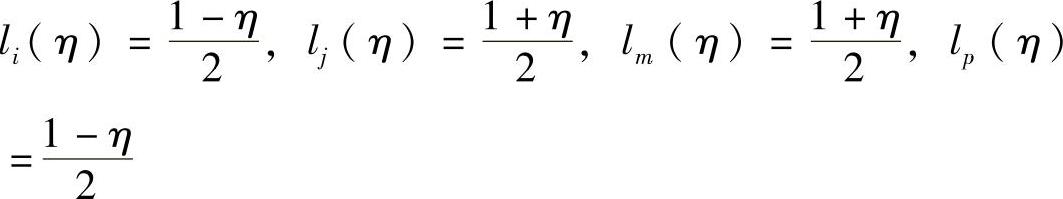
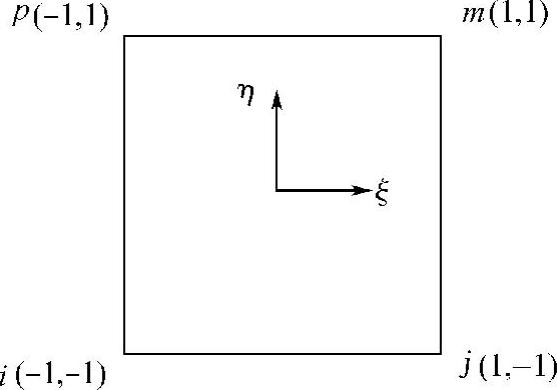
图5-2 自然坐标系中的正方形单元

在结点i上，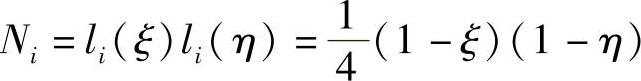

在总体坐标系下，结点i的形态函数为，

同样，可以得到其他三个结点上的形态函数

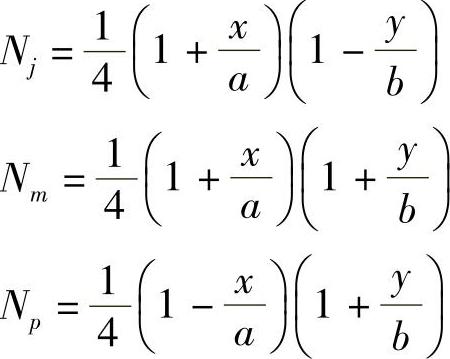
上述单元位移模式满足位移模式选择的基本要求：

1）反映了单元的刚体位移和常应变。

2）单元在公共边界上位移连续。

在矩形单元的边界上，坐标x和y的其中一个取常量，因此在边界上位移是线性分布的，由两个结点上的位移确定。

与三结点三角形单元相比，四结点矩形单元的位移模式是坐标的二次函数，也能够提高计算精度，但也有显著的缺点，两种单元的比较如表5-1所示。

表5-1 三结点三角形单元与四结点矩形单元比较