不增加单元数量而通过提高单元位移函数所包含的多项式项的阶次，在单元内部更准确地反映位移变化，从而提高计算精度，这种方法被称为p方法（p-method）结构分析。通常增加单元的结点数目就能提高位移插值函数的阶次。

用六结点三角形单元（Plane82）计算例4-1问题的应力分布。如图4-17所示，单元数目为196。在垂直对称面上x方向正应力分量S_x的变化如图4-18所示，最大值为160.160MPa。

图4-17 六结点三角形单元网格

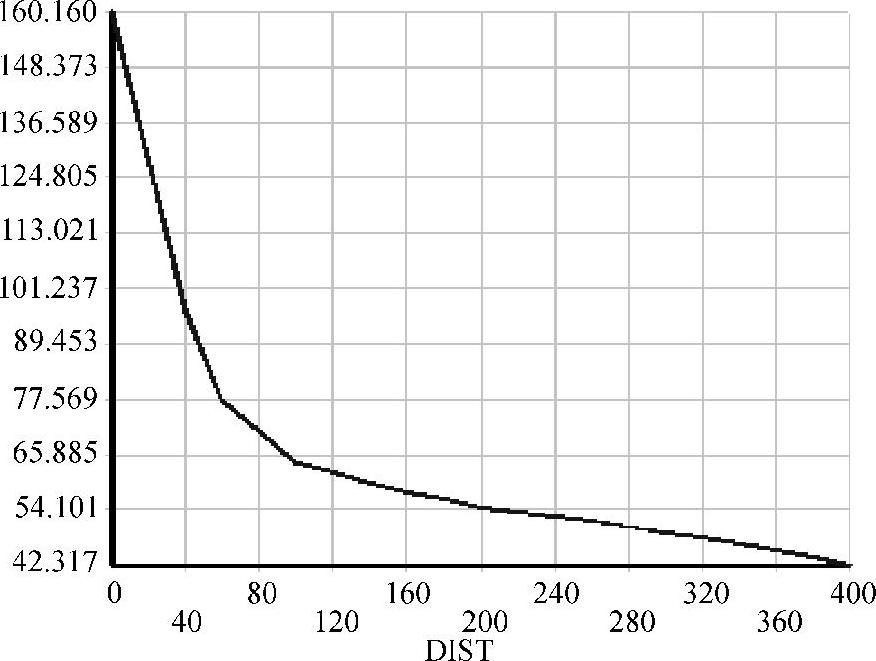
图4-18 六结点三角形单元的正应力分量S_x的变化

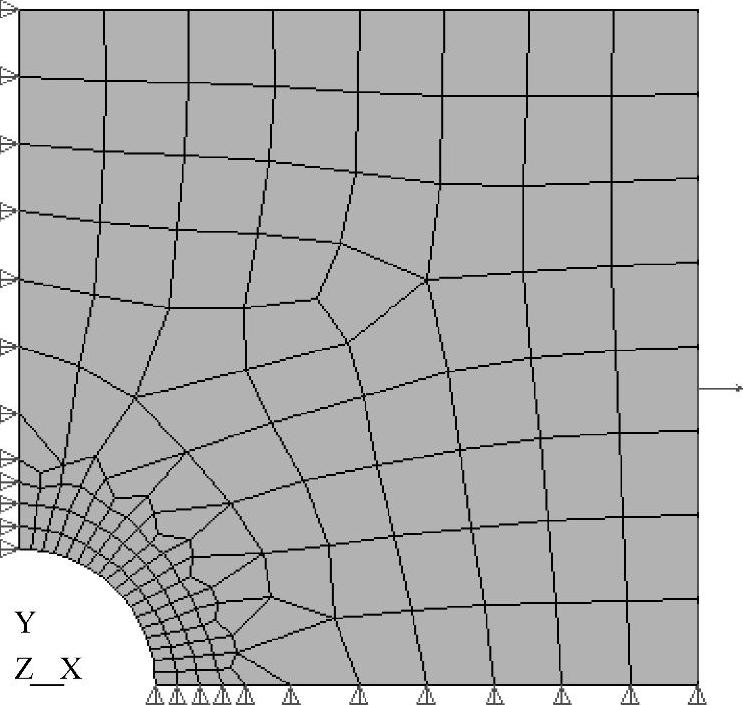
图4-15 加密后的四结点四边形单元网格

(www.daowen.com)

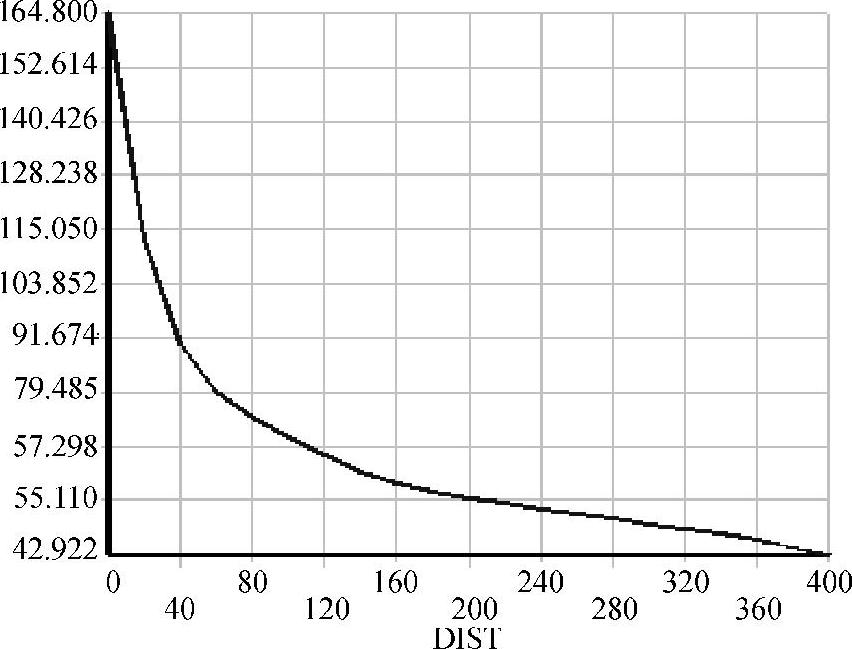
图4-16 加密后四结点四边形单元的正应力分量S_x的变化

同样用八结点四边形单元计算例4.1问题的应力分布，单元划分方案与图4-18的单元划分方案相同，如图4-19所示。在垂直对称面上x方向正应力分量S_x的变化如图4-20所示，最大值为155.869MPa。

把图4-20中的计算结果与图4-14的计算结果做对比，把图4-18的计算结果与图4-12的计算结果做对比，可以发现：采用六结点三角形单元的计算精度比采用三结点三角形单元的计算精度要高；采用八结点四边形单元的计算精度比采用四结点四边形单元的计算精度要高。主要原因就是六结点三角形单元和八结点四边形单元的位移插值函数的阶次更高。

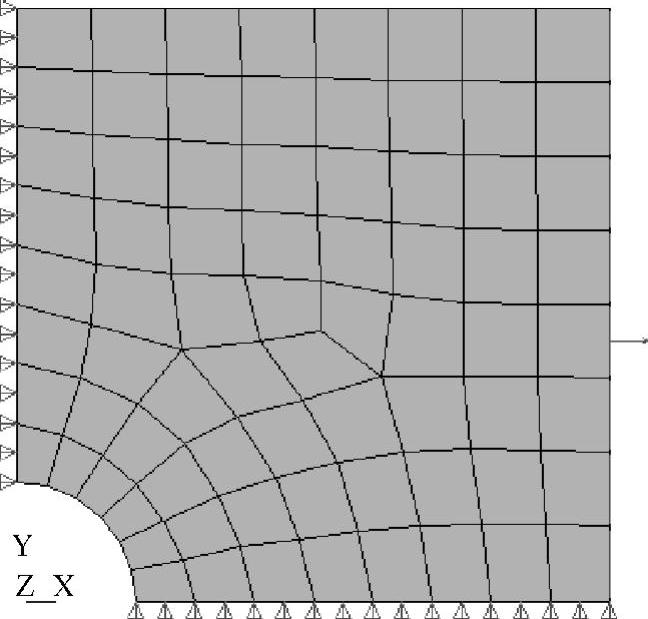
图4-19 八结点四边形单元网格

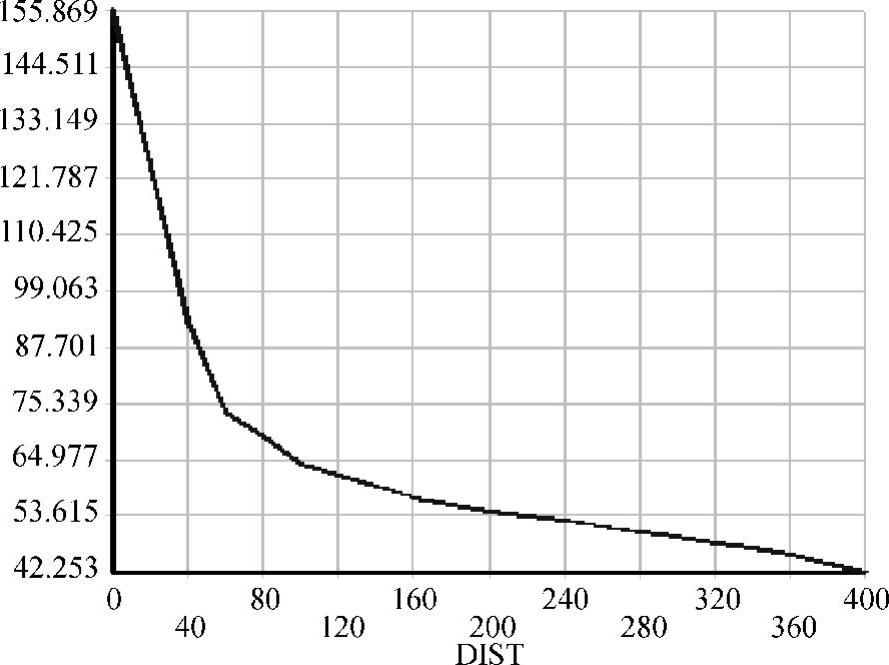
图4-20 八结点四边形单元的正应力分量S_x的变化