有限元方法是一种近似算法，有限元分析的计算结果与真实解答存在一定偏差。这种偏差的主要来源是建立模型的近似处理，以及单元离散化所带来的计算误差。主要采用两种方法来降低单元离散化产生的误差：一是增加单元数量，被称为h方法；二是提高单元位移函数多项式的阶次，被称为p方法。

在进行结构分析的时候，增加单元数量（或密度），用更多的分片区域来近似真实解，更好地反映未知函数的变化，这种方法被称为h方法（h-method）结构分析。例4-1带中心圆孔方板问题计算出的应力分布表明，在圆孔边缘处应力分量S_x变化较大。按照h方法，为提高计算精度可以采用整体加密单元网格的方法，也可以采用在圆孔边缘处加密单元网格的方法。

例4-3：对于例4-1中的带中心圆孔方板，在圆孔的边缘处加密三角形单元网格。显示x方向正应力在垂直方向对称轴上的分布。

如图4-9所示，把圆孔边单元局部细化后，三结点三角形单元数目为268。在垂直对称面上x方向正应力分量S_x的变化如图4-10所示，计算出的最大的正应力值由127.44MPa增加到139.892MPa。

图4-9 边缘加密的三角形单元网格

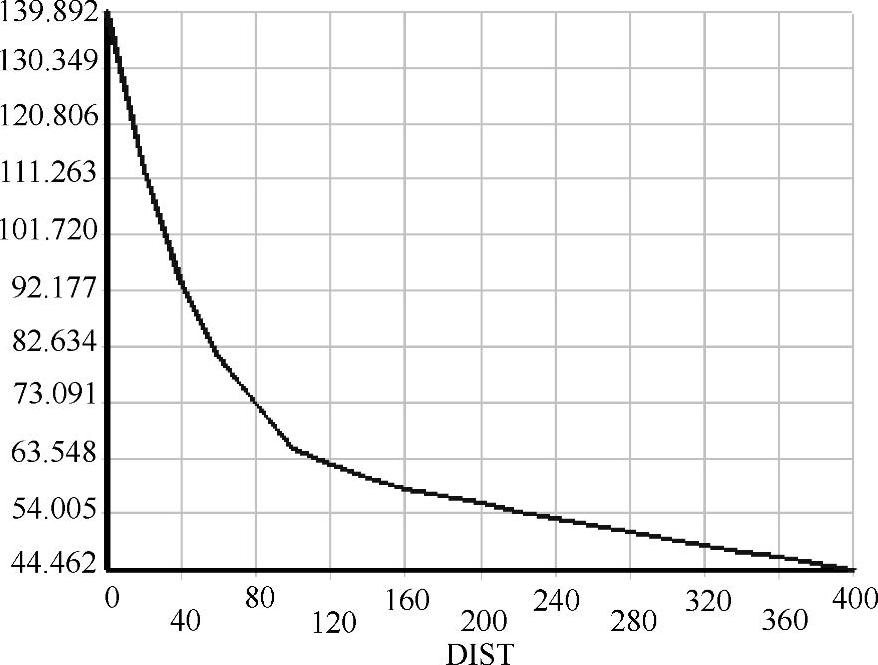
图4-10 边缘加密三角形单元网格后正应力分量S_x的变化

例4-4：对于例4-1中的带中心圆孔方板，整体加密三角形单元网格，显示x方向正应力在垂直方向对称轴上的分布。

如图4-11所示，整体加密后的三结点三角形单元数目为436。在垂直对称面上x方向正应力分量S_x的变化如图4-12所示，计算出的最大正应力值由127.44MPa增加到138.593MPa。将两种加密方案的计算结果相比较，采用内孔边缘加密的方案能够用比较少的单元获得精度相当的计算结果。

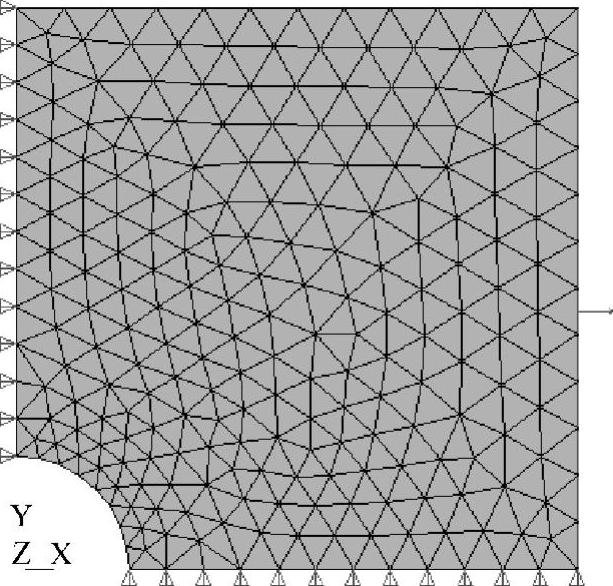
图4-11 整体加密的三角形单元网格(www.daowen.com)

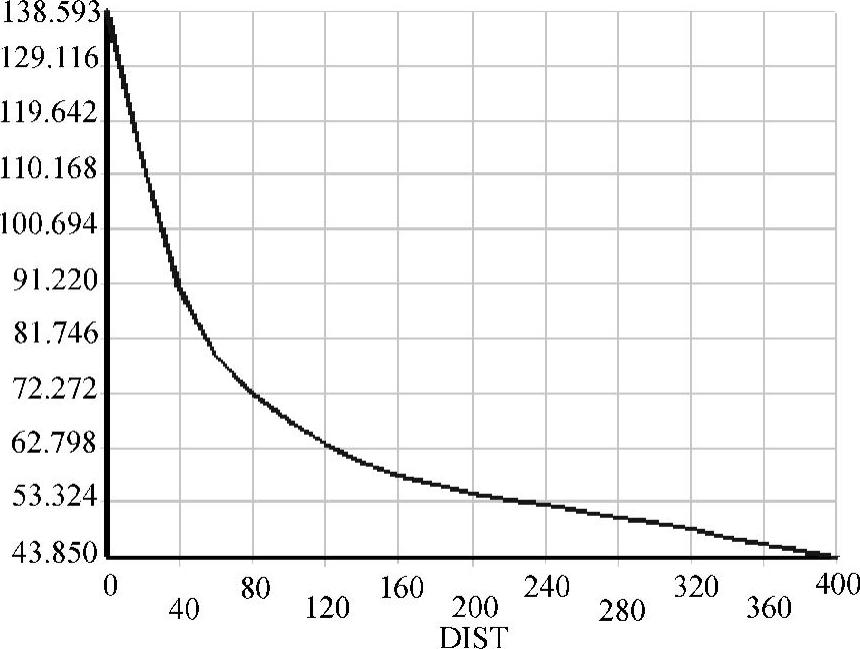
图4-12 整体加密三角形单元网格后正应力分量S_x的变化

为了对比不同类型单元的计算结果，接下来用四边形四结点单元建立带中心孔方板的有限元模型，比较垂直对称轴上x方向正应力的计算结果。

例4-5：对于例4-1中的问题，保持在边界线段上所设置的单元边数不变，而采用四结点四边形单元（在ANSYS软件中选择PLANE42单元）计算垂直方向对称轴上的x方向正应力分量的分布。

如图4-13所示，四边形单元数目为76。垂直方向对称轴上的x方向正应力分量S_x的变化如图4-14所示，最大的正应力值为148.372MPa。

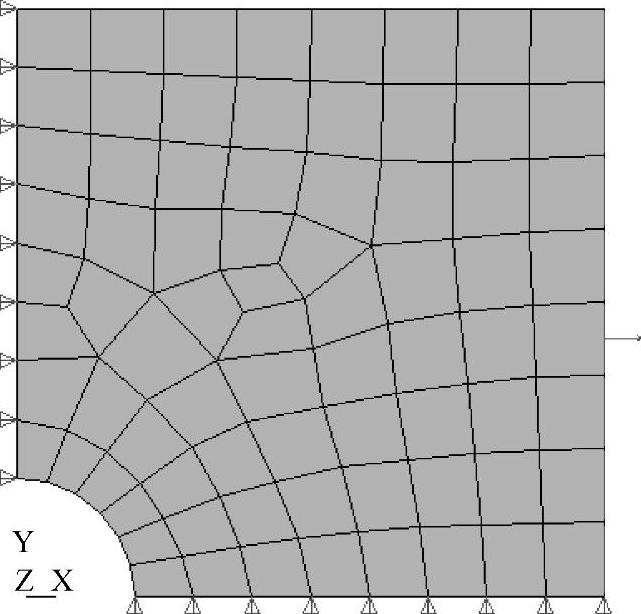
图4-13 四结点四边形单元网格

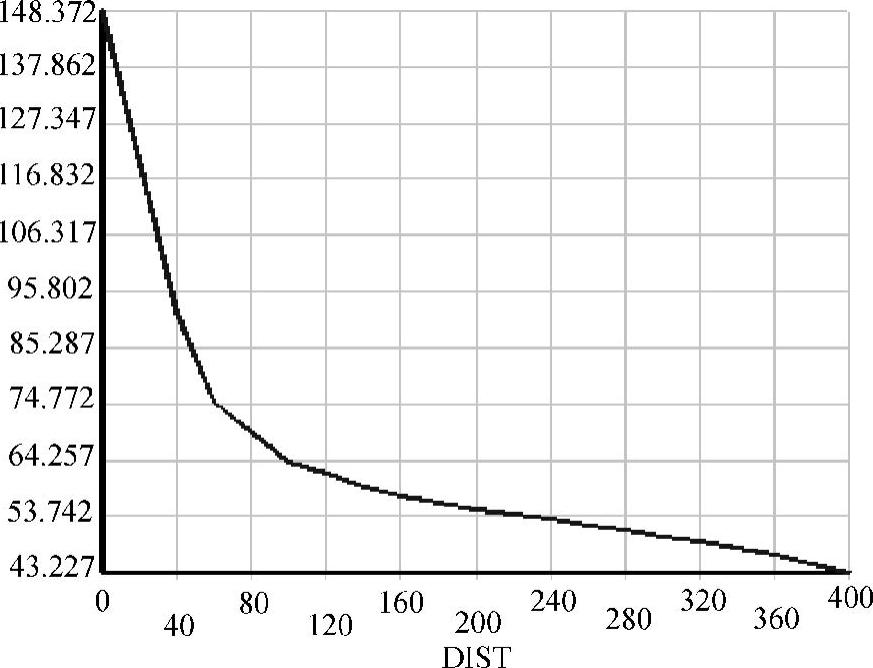
图4-14 采用四结点四边形单元后正应力分量S_x的变化

例4-6：对于例4-1的问题，仍然用四结点四边形单元（PLANE42），在圆孔边缘加密单元，计算垂直方向对称轴上的x方向正应力分量的分布。

如图4-15所示，加密后的单元数目为148。垂直方向对称轴上的x方向正应力分量S_x的变化如图4-16所示，最大值为164.800MPa。