用有限元方法分析复杂工程问题时，结点的数目比较多，整体刚度矩阵的阶数通常也是很高的。那么，是否在进行计算时要保存整体刚度矩阵的全部元素？能否根据整体刚度矩阵的特点提高计算效率？

整体刚度矩阵具有以下几个显著的特点：对称性、稀疏性和非零元素带形分布。

1）对称性。由单元刚度矩阵的对称性和整体刚度矩阵的集成规则，可知整体刚度矩阵必为对称矩阵。利用对称性，只保存整体矩阵上三角部分的系数即可。

2）稀疏性。单元刚度矩阵的多数元素为零，非零元素的个数只占较小的部分。如图3-26所示的结构，结点2只和通过单元连接的1、3、4、5结点相关，结点5只和通过单元连接的2、3、4、6、8、9结点相关。由单元刚度矩阵的物理意义和整体刚度矩阵的形成方式可知，相关结点2、3、4、6、8、9及结点5本身产生位移时，才使结点5产生结点力，其余结点产生位移时不在该结点处引起结点力。在用分块形式表示的整体矩阵中，与相关结点对应的分块矩阵才能具有非零的元素，其他位置上的分块矩阵的元素为零，如图3-27所示。

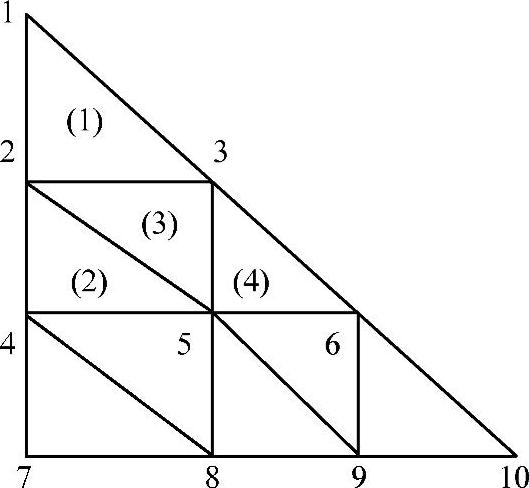
图3-26 由9个单元组成的结构

图3-27 整体刚度矩阵的分块矩阵示意

3）非零元素带形分布。在图3-27中，明显可以看出，整体刚度矩阵的非零元素分布在以对角线为中心的带形区域内，这种矩阵称为带形矩阵。

在包括对角线元素在内的半个带形区域内，每行具有的元素个数叫做半带宽，用d表示。

d=（相邻结点的编码的最大差值+1）×2

图3-26所示结构的相邻结点编码的最大差值为4，所以半带宽为10。(www.daowen.com)

设整体刚度矩阵K为一个n×n的矩阵，最大半带宽为d。利用带形矩阵的特点和对称性，只需要保存以d为固定宽度的上半带的元素，称为二维等带宽存储。进行存储时，把整体刚度矩阵K每行中的上半带元素取出，保存在另一个矩阵K^*的对应行中，得到一个n×d矩阵K^*。

把元素在K矩阵中的行、列编码记为r、s，在矩阵K^*中的行、列编码记为r^*、s^*，对应关系如下：

r^*=r，s^*=s-r+1

图3-28a所示为最大半带宽为d的整体刚度矩阵K，采用二维等带宽存储后得到如图3-28b所示的矩阵K^*。用新的方法存储后，K矩阵中的对角线元素保存在新矩阵中的第1列中，K矩阵中的r行元素仍然保存在新矩阵的r行中，K矩阵中的s列元素则按照新的列编码保存在新矩阵的不同列中。

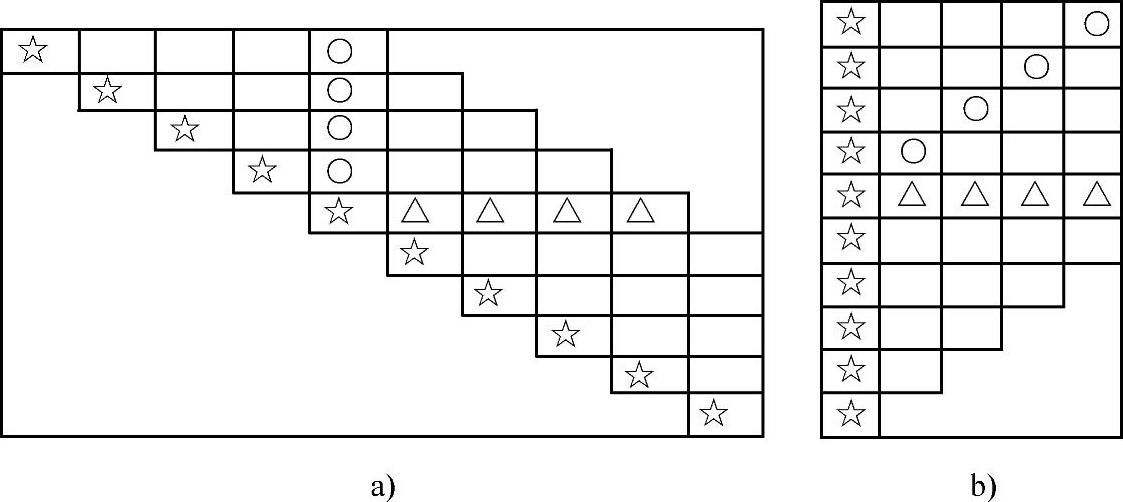
图3-28 二维等带宽存储示意图

采用二维等带宽存储，需要保存的元素

数量与K矩阵中的总元素数量之比为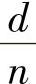。所存储的元素数量取决于最大半带宽d的值，d的值则由单元结点的编码方式决定。在采用二维等带宽存储时，仍然会保存一些零元素，但是采用这种方法时元素寻址很方便。

对于同样的有限元单元网格，按照图3-29a的结点编码，最大的半带宽为14；按照图3-29b的结点编码，最大的半带宽为18；按照图3-26的结点编码，最大的半带宽为10。

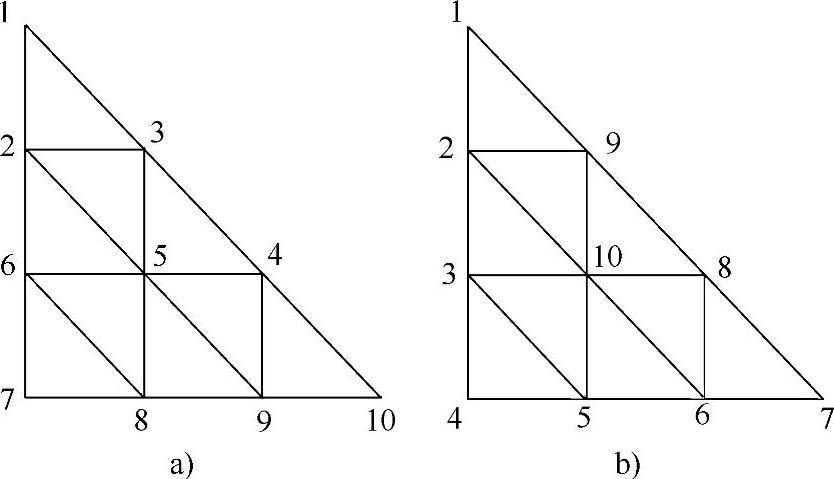
图3-29 不同结点编码方式对半带宽的影响