图3-24所示的结构的约束和载荷情况，如图3-25所示。结点1、4上有水平方向的位移约束，结点4、6上有垂直方向的约束，结点3上作用有集中力（P_x，P_y）。

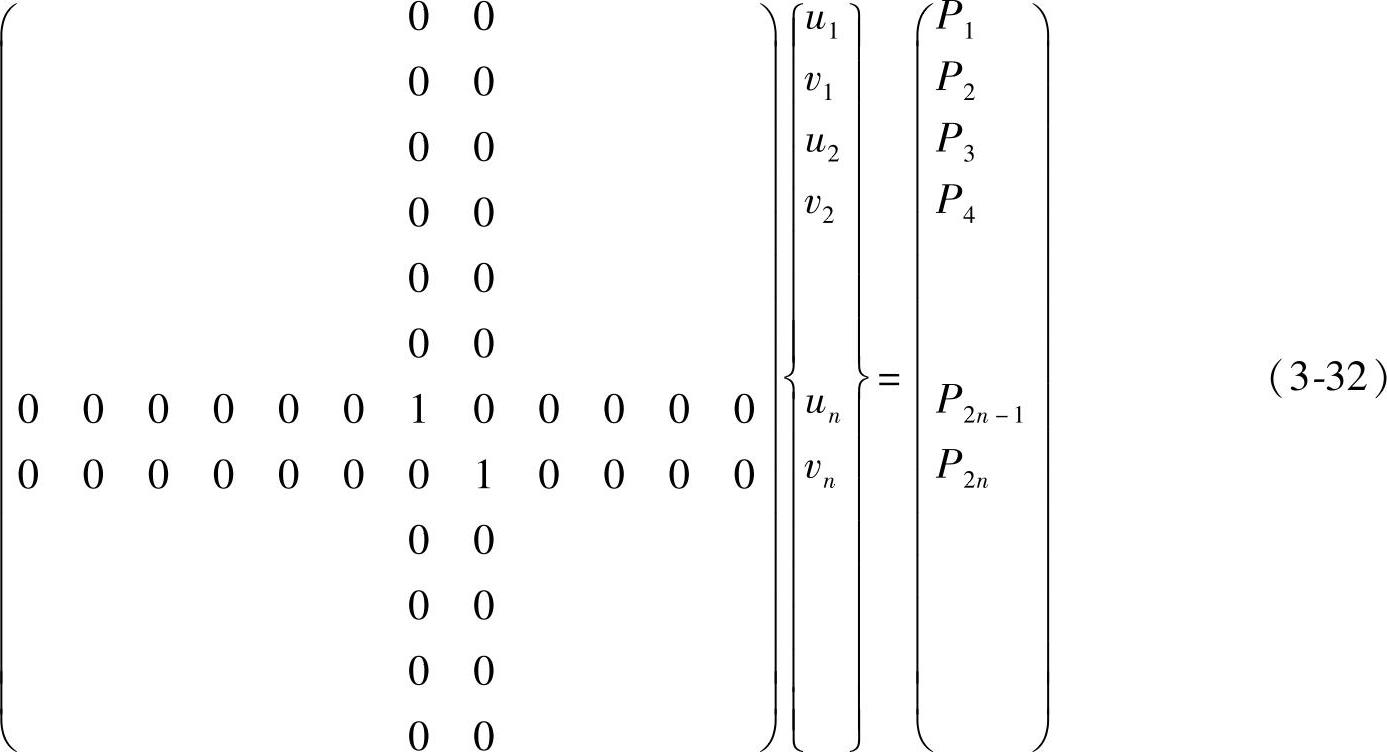
这样构成的结点平衡方程组，在右边向量{P}中存在未知量，因此在求解平衡方程之前，要根据结点的位移约束情况修改方程（3-29）。先考虑结点n有水平方向位移约束，与n结点水平方向对应的平衡方程为：

K_2n-1，1u₁+K_2n-1，2v₁+…+K_2n-1，2n-1u_n+K_2n-1，2nv_n+…=P_2n-1 （3-30）

根据支承情况，式（3-30）应该换成下面的方程：

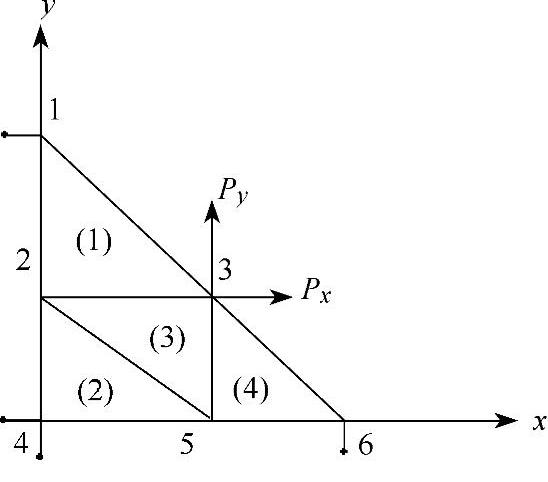
图3-25 有外载荷与约束条件的4单元结构

u_n=0 （3-31）

对比式（3-30）和式（3-31），在式（3-29）中应该做如下修正：

在[K]矩阵中，第2n-1行的对角线元素K_2n-1，2n-1改为1，该行中全部非对角线元素改为0；在{P}中，第2n-1个元素改为0。为了保持[K]矩阵的对称性，将第2n-1列的全部非对角元素也改为0。

同理，如果结点n在垂直方向有位移约束，则式（3-29）中的第2n个方程修改为，

v_n=0

在[K]矩阵中，第2n行的对角线元素改为1，该行中全部非对角线元素改为0；在{P}中，第2n个元素改为0。为了保持[K]矩阵的对称性，将第2n列的全部非对角元素也改为0。(www.daowen.com)

对图3-25所示结构的整体刚度在修改后可以得到以下的形式，

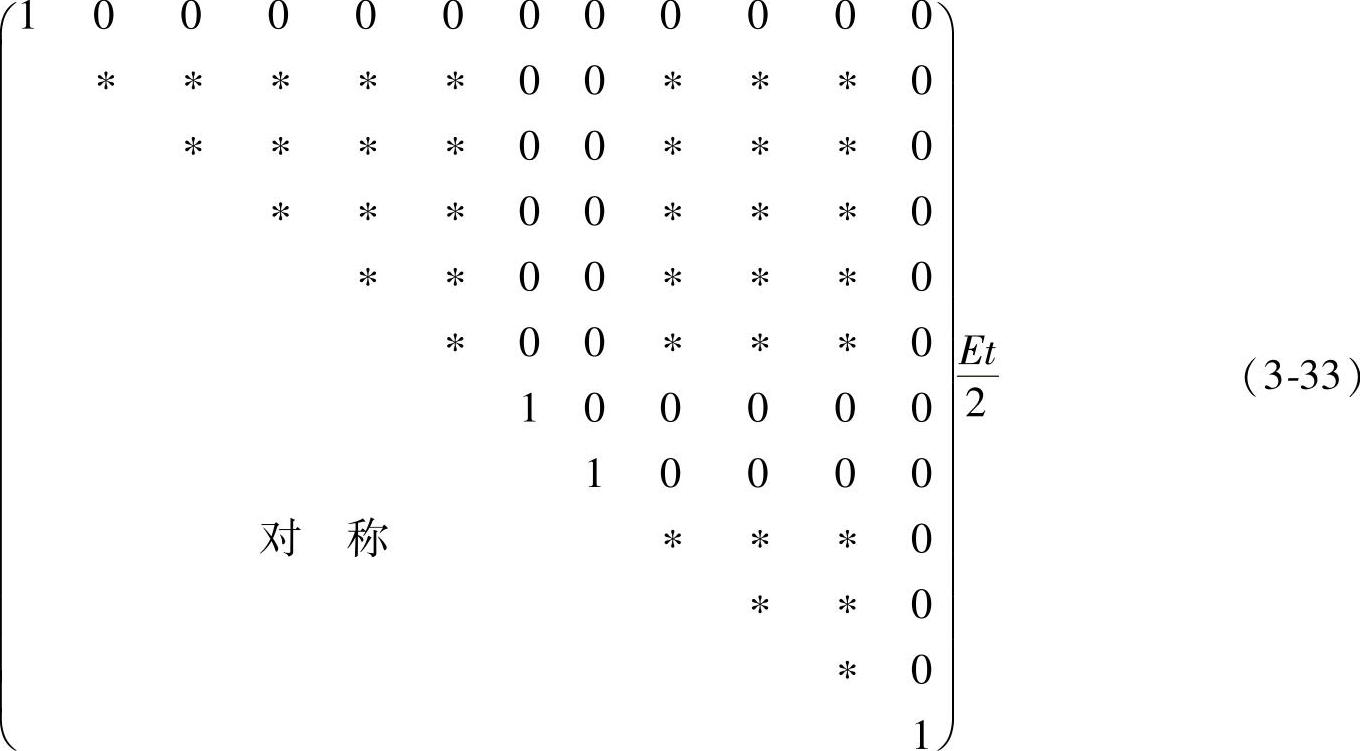
如果结点n处存在一个已知非零的水平方向位移u_n^*，这时的约束条件为，

u_n=u_n^* （3-34）

在[K]矩阵中，第2n-1行的对角线元素K_2n-1，2n-1乘上一个大数A，向量{P}中的对应换成AK_2n-1，2n-1u_n^*，其余的系数保持不变。

方程改为

K_2n-1，1u₁+K_2n-1，2v₁+…+AK_2n-1，2n-1u_n+K_2n-1，2nv_n+…=AK_2n-1，2n-1u_n^* （3-35）其中，A的取值要足够大，例如取10¹⁰。只有这样，方程（3-35）才能与方程（3-34）等价。

如果结点n处存在一个已知非零的垂直方向位移v_n^*，这时的约束条件为

v_n=v_n^*

也可以采用同样的方法修改整体刚度矩阵。