1）单元刚度矩阵中的每个分块放到在整体刚度矩阵中的对应位置上，得到单元的扩大刚度矩阵。单元刚度矩阵元素取决于单元结点的局部编号顺序，必须知道单元结点的局部编号与该结点在整体结构中的总体编号之间的关系，才能得到单元刚度矩阵中的每个分块在整体刚度矩阵中的位置。将单元刚度矩阵中的每个分块按总体编码顺序重新排列后，可以得到单元的扩大矩阵。
在编制有限元程序时，可以用一个二维数组来保存三结点三角形单元结点的局部编号与该结点在整体结构中的总体编号之间的关系。假定最大单元数目为NELEM，用Fortran语言可以定义以下数组，
DIMENSION NEC（NELEM，3）
数组的行与单元对应，数组的第1列为单元中I结点的整体编号，第2列为单元中J结点的整体编号，第3列为单元中M结点的整体编号。例如，
NEC（I，1）=5，表示第I个单元中I结点的整体编号为5；
NEC（I，2）=2，表示第I个单元中J结点的整体编号为2；
NEC（I，3）=4，表示第I个单元中M结点的整体编号为4。
假定图3-24所示结构中单元结点的局部编号与整体的对应关系如表3-1所示。
表3-1 局部编号与整体的对应关系
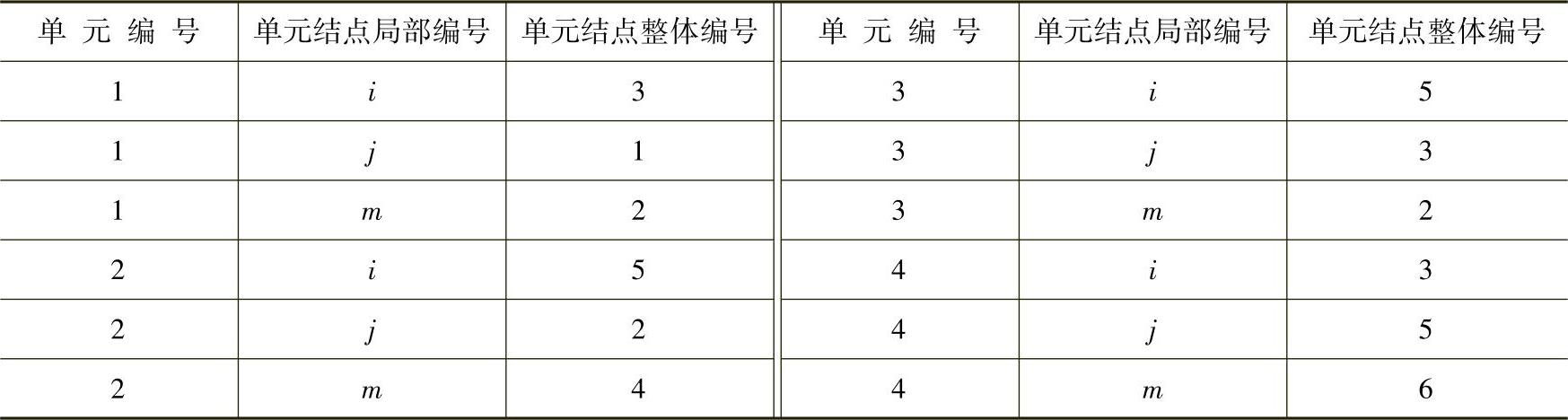
单元（2）的单元扩大矩阵（K）（2）的分块矩阵形式如表3-2所示，只列出非零的分块。
表3-2单元（2）的单元扩大矩阵
（续）
(www.daowen.com)
2）将全部单元的扩大矩阵相加得到整体刚度矩阵。
K=K（1）+K（2）+K（3）+K（4）
整体刚度矩阵的分块形式如表3-3所示。
整体刚度矩阵K求出后，结构上的结点力可以表示为F=Kδ
表3-3 整体刚度矩阵
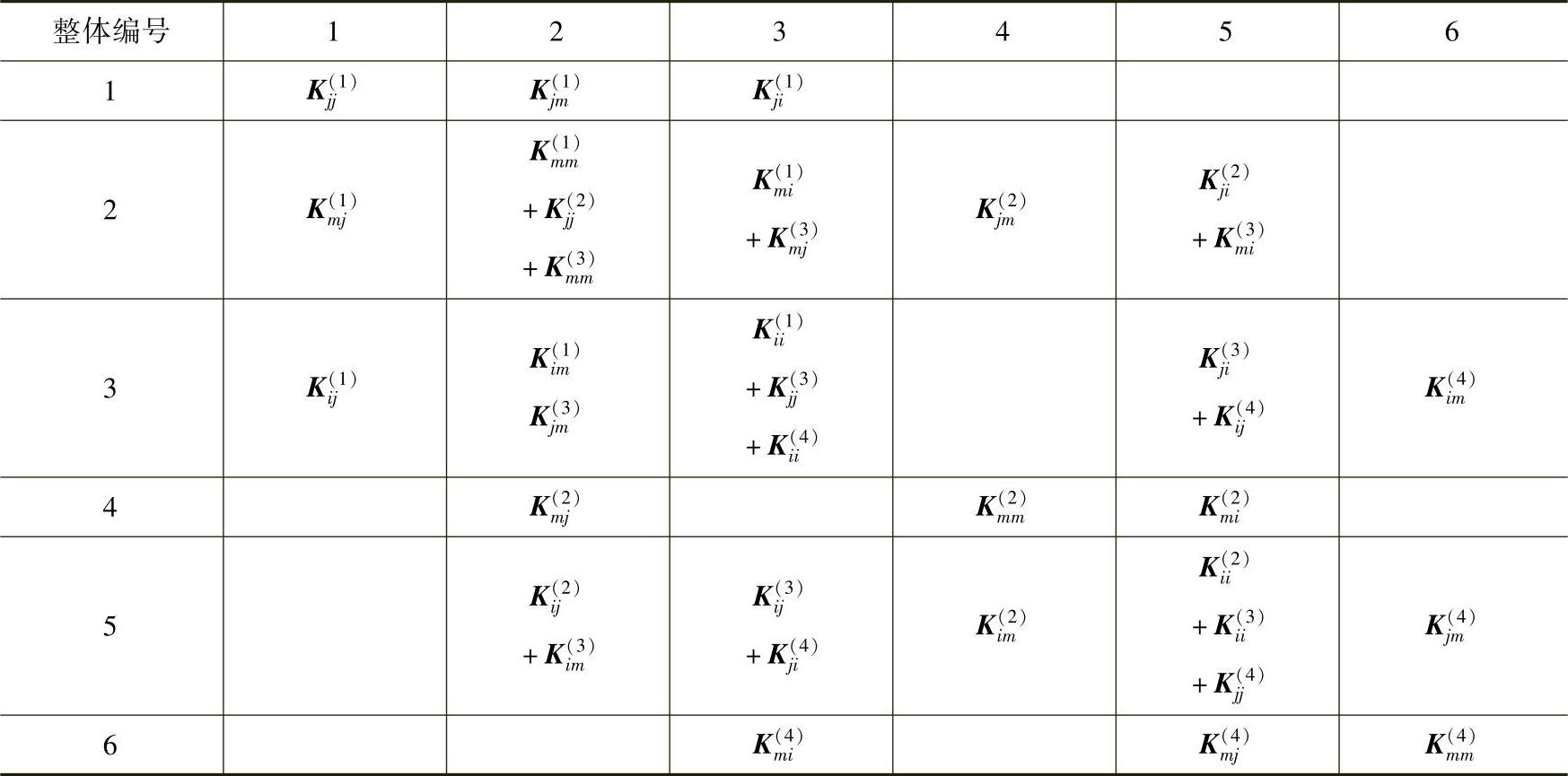
根据力的平衡，结点上的结点力与结点载荷或约束反力平衡。用P表示结点载荷和位移约束的支反力，则可以得到结点的平衡方程：
Kδ=P （3-29）
用虚功原理，我们重新描述整体刚度矩阵的形成方法。假定弹性体总共划分为m个单元，单元刚度矩阵为ki，总体结点位移为f，单元结点位移为fi，总体载荷R，单元结点力Qi。
弹性体外力总虚功δW等于各单元外力虚功δWi之和，
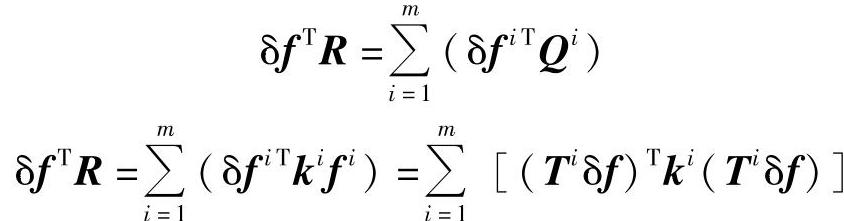
其中，Ti为单元结点局部编号与整体编号的转换矩阵，
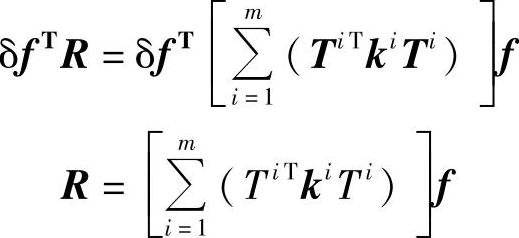
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
