【摘要】:将应力矩阵分块表示为,应用虚功原理可以建立单元结点位移与结点力的关系矩阵,即单元刚度矩阵。单元的结点力记为Fe=T单元的虚应变为ε*=Bδ*e单元的外力虚功为(δ*e)TFe单元的内力虚功为由虚功原理可得定义为单元刚度矩阵。
根据单元的位移函数,
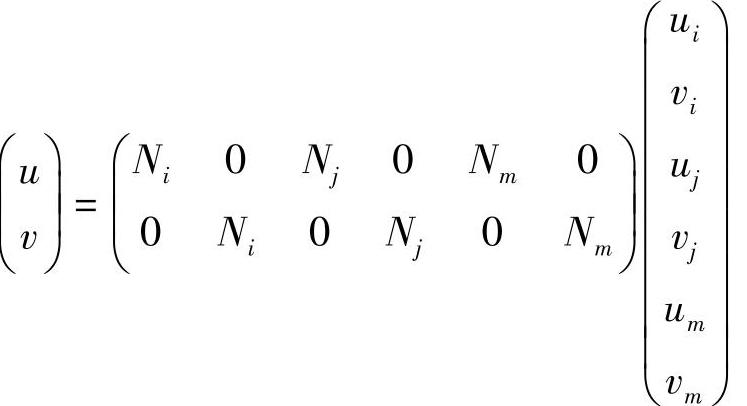
由几何方程可以得到单元的应变表达式,
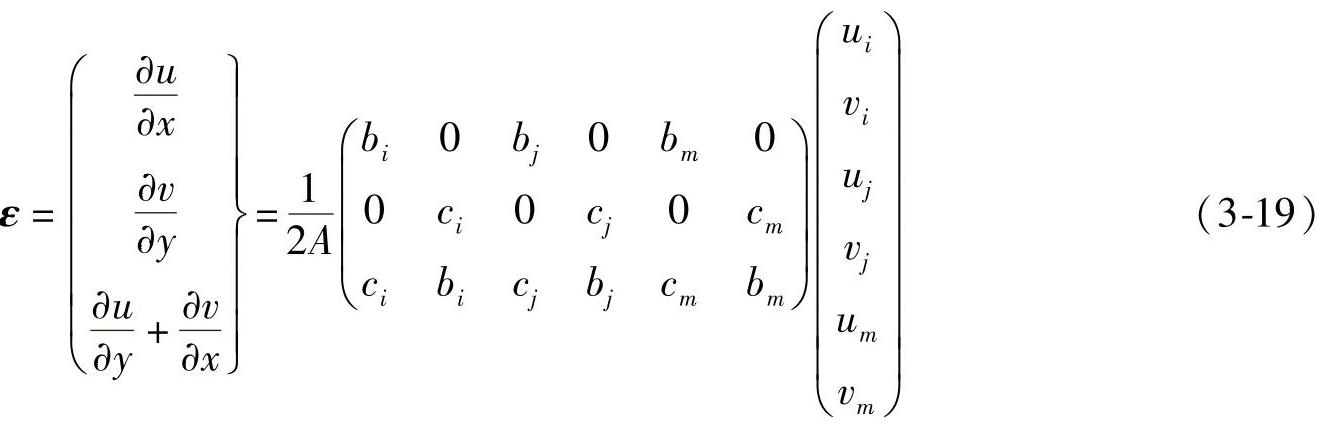
记为ε=Bδe,B矩阵称为几何矩阵。
B矩阵可以表示为分块矩阵的形式B=〔BiBjBm〕

由物理方程,可以得到单元的应力表达式,
σ=Dε=DBδe (3-21)
D称为弹性矩阵,对于平面应力问题,
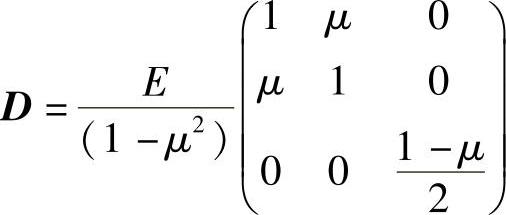
定义S=DB为应力矩阵。
将应力矩阵分块表示为,

应用虚功原理可以建立单元结点位移与结点力的关系矩阵,即单元刚度矩阵。
虚功原理:在外力作用下处于平衡状态的弹性体,如果发生了虚位移,则所有外力在虚位移上做的虚功等于内应力在虚应变上做的虚功。
单元的结点力记为Fe=(UiViUjVjUmVm)T
单元的虚应变为ε=Bδe
单元的外力虚功为(δe)TFe
单元的内力虚功为 (https://www.daowen.com)
(https://www.daowen.com)
由虚功原理可得
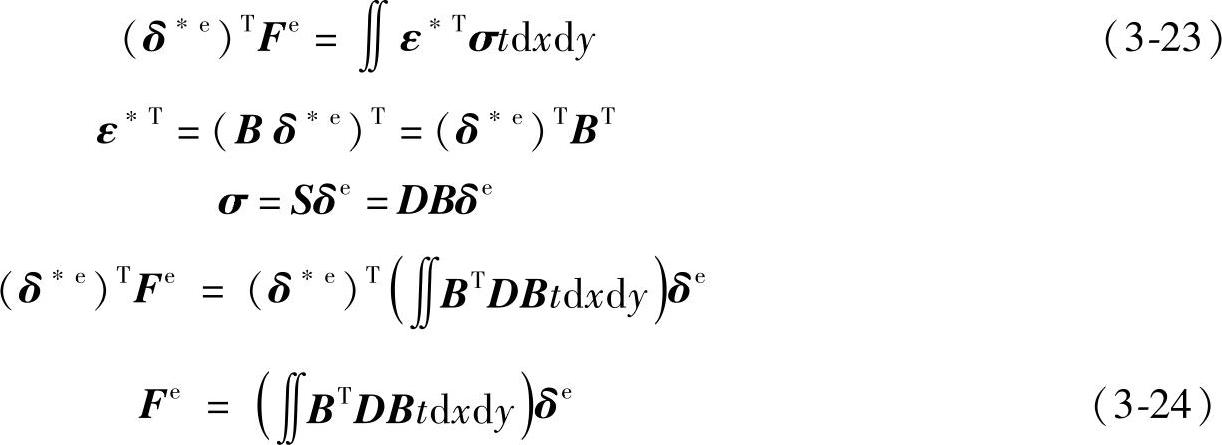
定义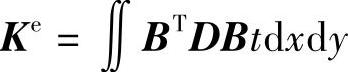 为单元刚度矩阵。
为单元刚度矩阵。
在三结点等厚三角形单元中B和D的分量均为常量,则单元刚度矩阵可以表示为
Ke=BTDBtA (3-25)
单元刚度矩阵表示为分块矩阵:

其中的一个分块为,

对于平面应力问题,
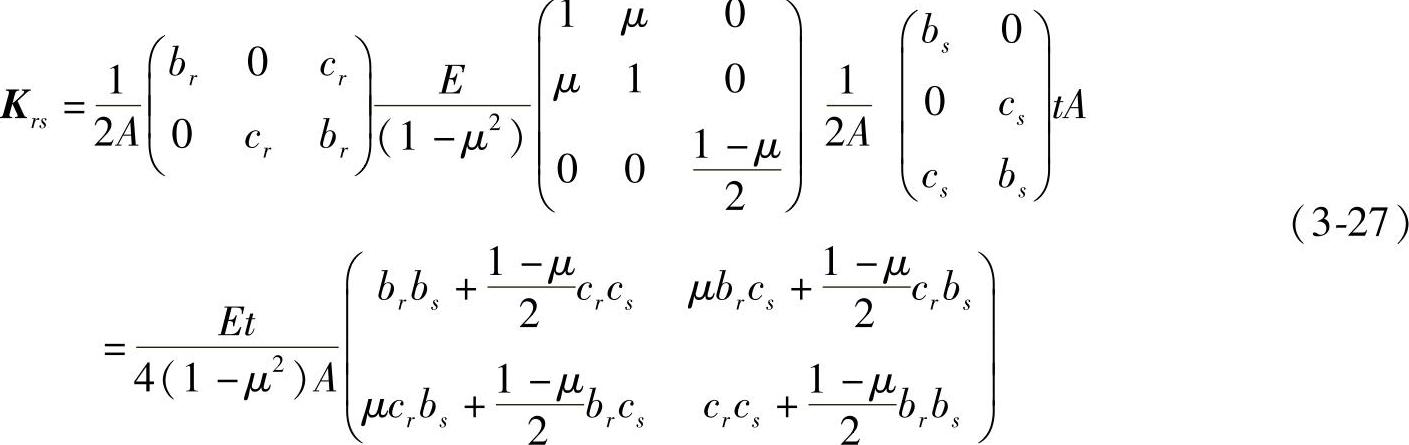
例3-6:如图3-23所示,属于平面应力问题的弹性体被划分成3个单元、5个结点。单元结点的局部编号顺序为e1(1,2,3);e2(2,4,5);e3(2,5,3)。求单元1的单元刚度矩阵。
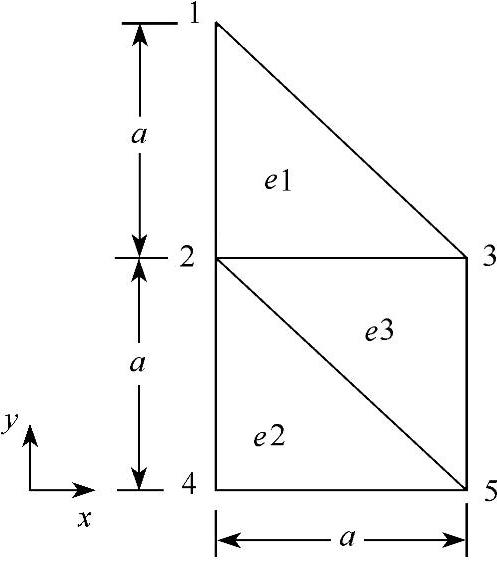
图3-23 简单的平面应力问题
对于单元1,
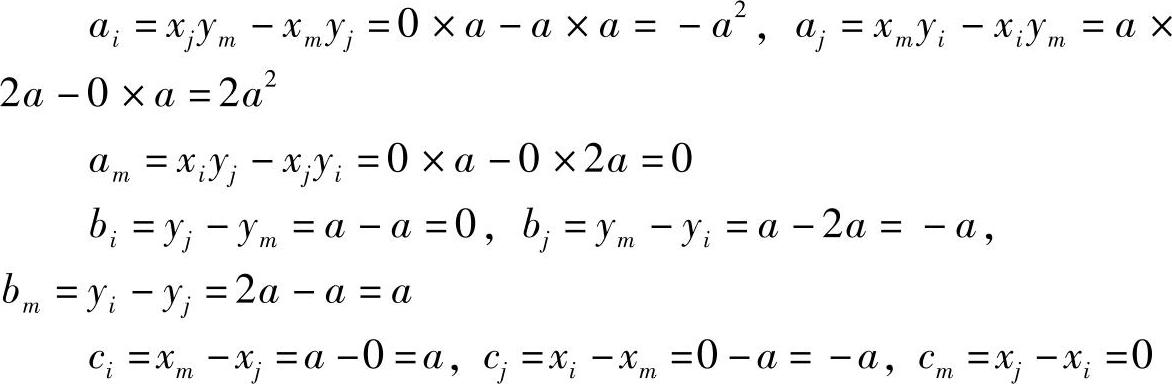
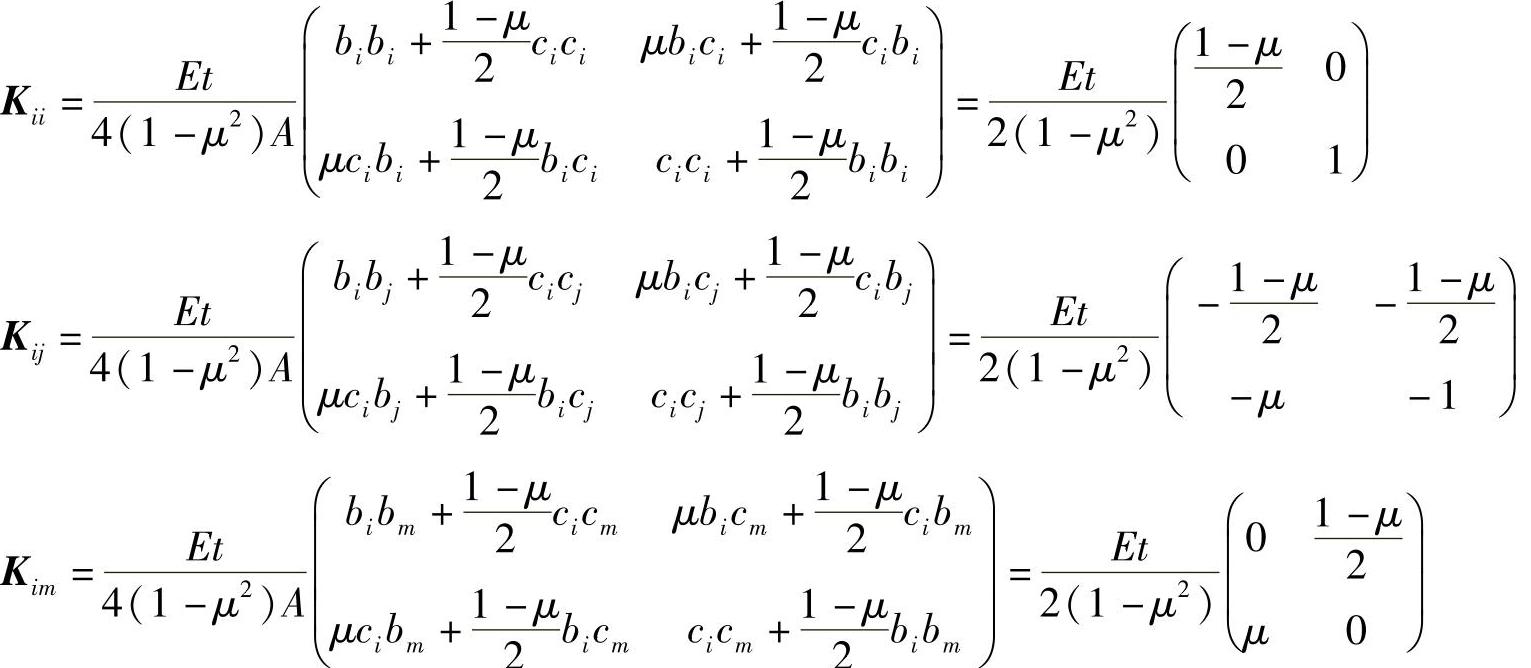


免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







