【摘要】:静力等效是指原载荷与移置后的载荷在任意虚位移上做的虚功相等。;同理,,例3-5:在均质、等厚的三角形单元IJM的IJ边上作用有沿x方向按三角形分布的载荷,求将分布载荷移置到各结点后的结点载荷,如图3-22所示。
有限元法的求解对象是单元的组合体,因此作用在弹性体上的所有外力都需要移置到相应的结点上成为结点载荷。载荷移置要满足静力等效原则。静力等效是指原载荷与移置后的载荷在任意虚位移上做的虚功相等。
单元的虚位移可以用结点的虚位移δe表示为,
f=Nδe (3-15)
令结点载荷为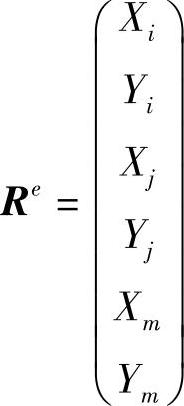
(1)集中力的移置 如图3-21所示,在单元内任意一点作用集中力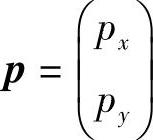
由虚功相等可得,(δe)TRe=(δe)TNTp
(δe)T[Re-NTp]=0
由于虚位移是任意的,则
Re=NTp (3-16)
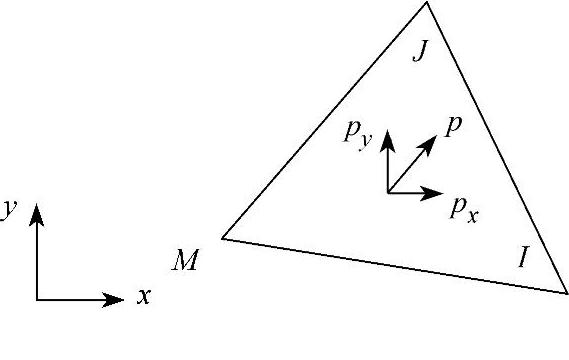
图3-21 集中载荷作用的单元
例3-3:在均质、等厚的三角形单元IJM的任意一点P(xP,yP)上作用有集中载荷。把集中载荷移置到三个单元结点上。
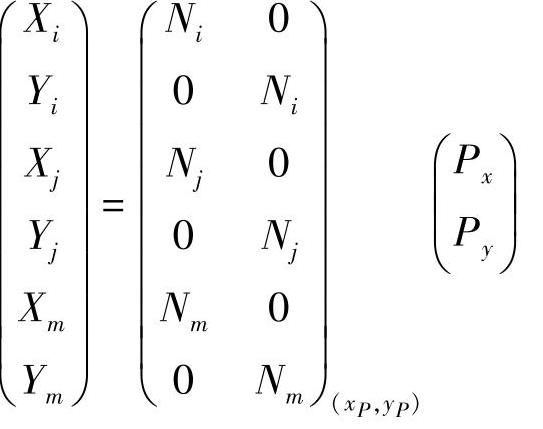
(2)体力的移置 令单元所受的均匀分布体力为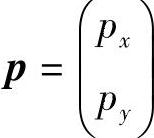
由虚功相等可得,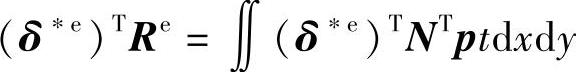
结点虚位移不随坐标变化,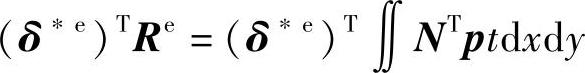
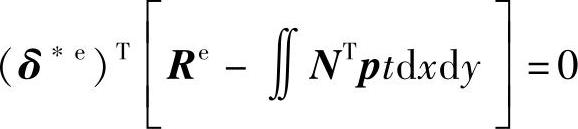
由于虚位移是任意的,则

面积坐标在三角形单元上的全积分公式如下(https://www.daowen.com)

(3)分布面力的移置 设在单元的边上分布有面力p=〔X,Y〕T,同样可以得到结点载荷,
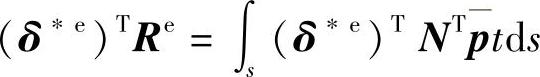
结点虚位移不随坐标变化,

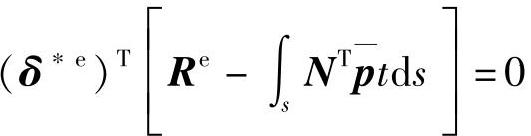
由于虚位移是任意的,则

例3-4:设有均质、等厚的三角形单元IJM,受到沿y方向的重力载荷qy的作用。求均布体力移置到各结点的载荷。

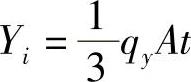 ;同理,
;同理,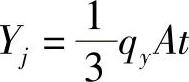 ,
,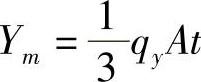
例3-5:在均质、等厚的三角形单元IJM的IJ边上作用有沿x方向按三角形分布的载荷,求将分布载荷移置到各结点后的结点载荷,如图3-22所示。
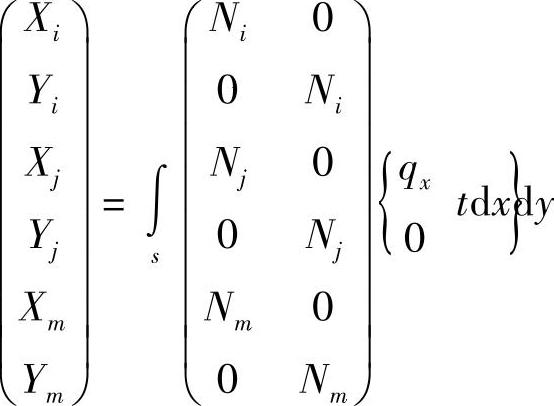
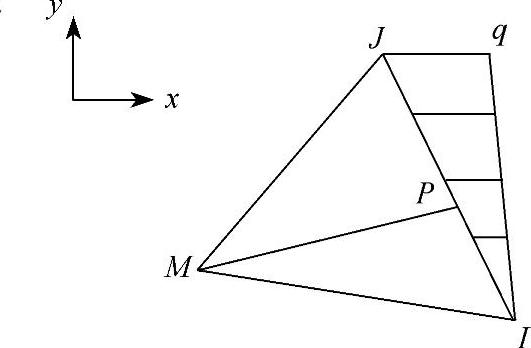
图3-22 分布面力的移载
取局部坐标s,在I点s=0,在J点s=L,L为IJ边的长度。P为IJ上的一点,以局部坐标表示P点的插值函数为
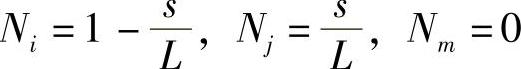
载荷为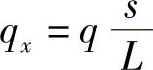
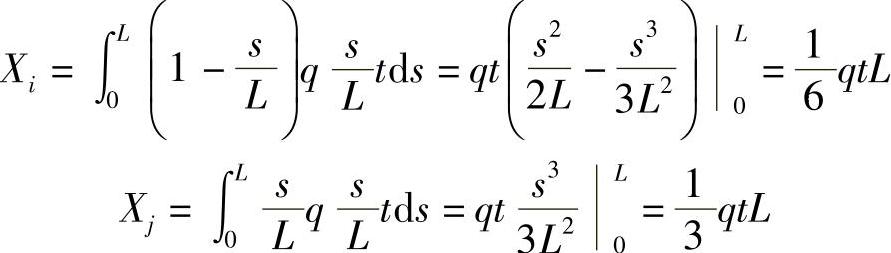
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







