有限元分析基础与应用教程：单元位移函数的重要性

根据有单限元法的基本思路，对于连续体，先进行必要的简化，再划分为有限个单元组成的离散体。单元之间通过单元结点相连接。由单元、结点、结点连线构成的集合称为网格。通常把平面问题划分成三角形（Triangular）或四边形（Quadrilateral）单元的网格，把三维实体划分成四面体（Tetrahedron）或六面体（Hexahedron）单元的网格。

带方孔的长方形钢制等厚度薄板，受到均布轴向拉力q的作用，薄板的厚度为d，拉力沿厚度方向均匀分布。如图3-15所示，可以用三角形单元或四边形单元划分成网格。

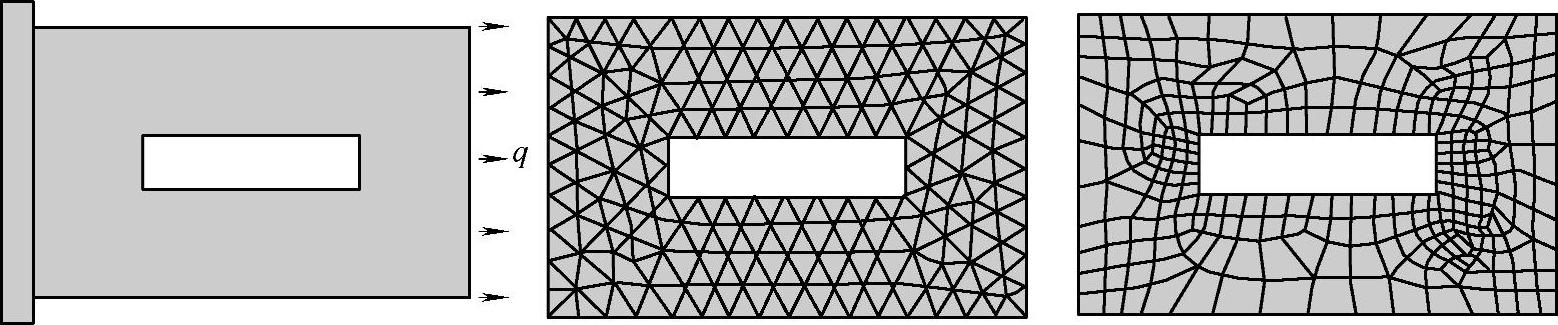
图3-15 弹性力学平面问题的网格划分

根据对弹性力学平面问题的分析，如果求解出弹性体内的位移分布，那么就可以求解出弹性体的变形与内力分布。整个弹性体内实际的位移分布可以用各单元内的位移分布函数来分块近似地表示。可以假定一个函数来表示单元内的位移分布，这个函数称为单元位移函数、或单元位移模式。

对于弹性力学平面问题，单元位移函数可以用完备的多项式表示

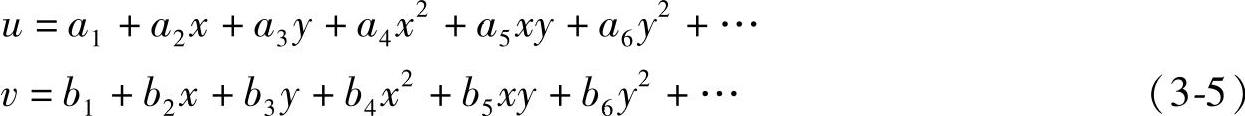
多项式中包含的项数越多，就越接近实际的位移分布，越精确。多项式具体取多少项，由单元形式来确定。即以结点位移来确定位移函数中的待定系数。

如图3-16所示的三结点三角形单元，结点I、J、M的坐标分别为（x_i，y_i）、（x_j，y_j）、（x_m，y_m），结点位移分别为（u_i，v_i）、（u_j，v_j）、（u_m，v_m）。六个结点位移只能确定六个多项式的系数，所以三结点三角形单元的位移函数如下，

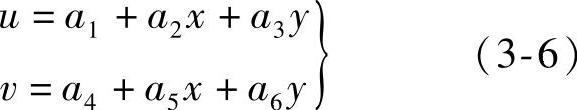
将三个结点上的坐标和位移分量代入式（3-6）就可以将六个待定系数用结点坐标和位移分量表示出来。将水平位移分量和结点坐标代入式（3-6）中的第一式，

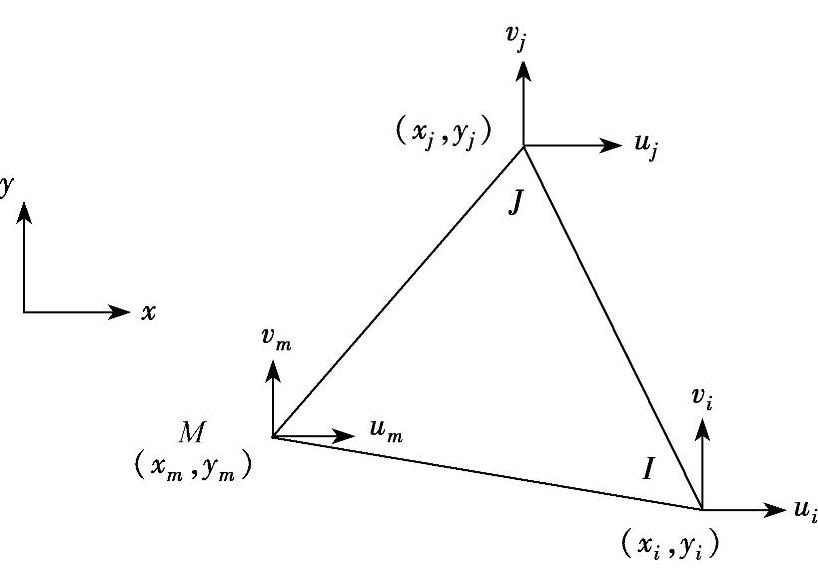
图3-16 三结点三角形单元

u_i=a₁+a₂x_i+a₃y_i

u_j=a₁+a₂x_j+a₃y_j

u_m=a₁+a₂x_m+a₃y_m

写成矩阵形式，

令，，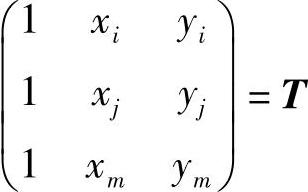

则有，

式中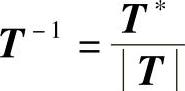，，|T|=2A，A为三角形单元的面积。

T的伴随矩阵为，

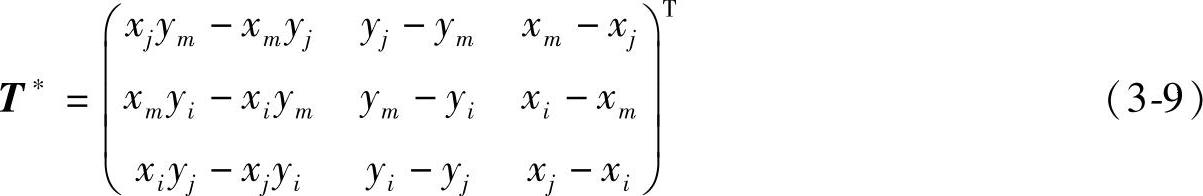
令，a_i=x_jy_m-x_my_j，b_i=y_j-y_m，ci=x_m-x_j

将下标按照结点的逆时针排列顺序i-＞j-＞m-＞i轮换得到，

a_j=x_my_i-x_iy_m，b_j=y_m-y_i，c_j=x_i-x_m

a_m=x_iy_j-x_jy_i，b_m=y_i-y_j，c_m=x_j-x_i

得到，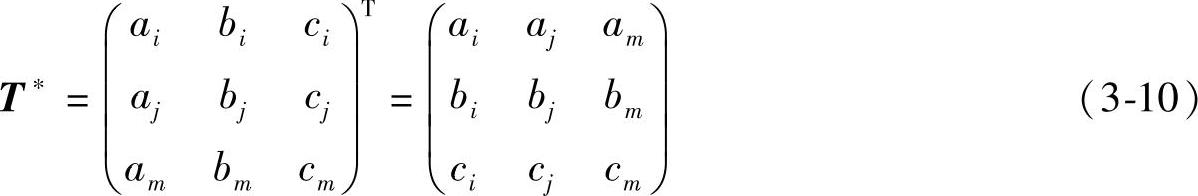

由式（3-8）得到，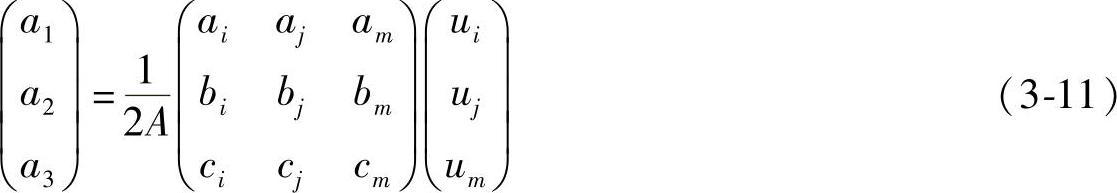

同样，将垂直位移分量与结点坐标代入式（3-6）中的第二式，可得，

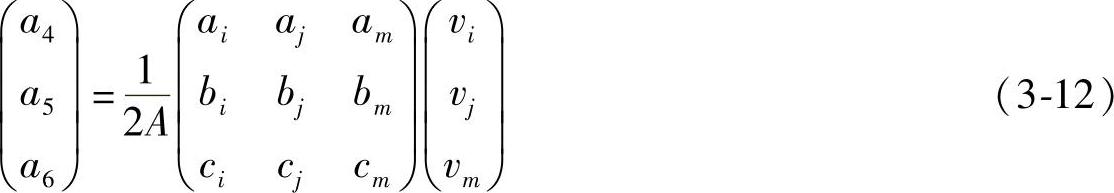
将式（3-11）、式（3-12）代回式（3-6）整理后可得，

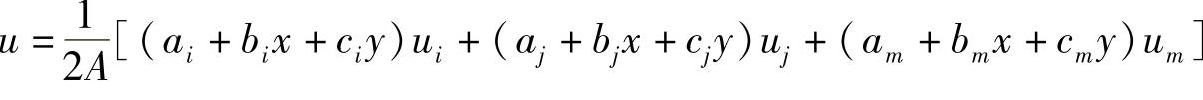
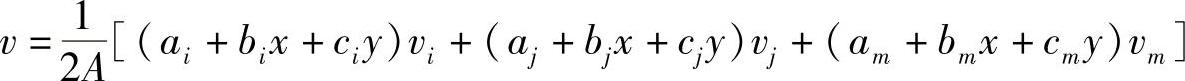
令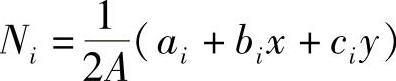，（下标按照i，j，m轮换）

可得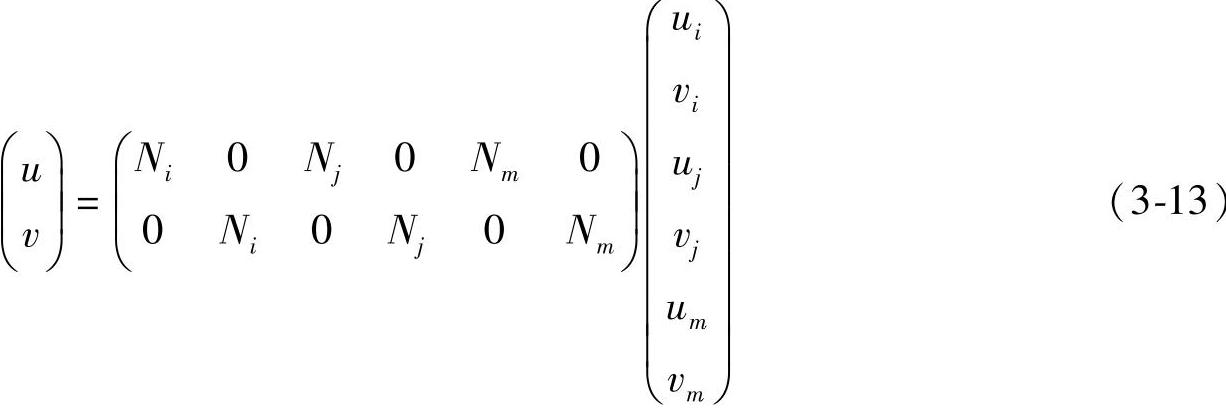

单元内的位移记为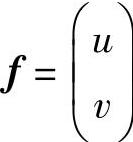

单元的结点位移记为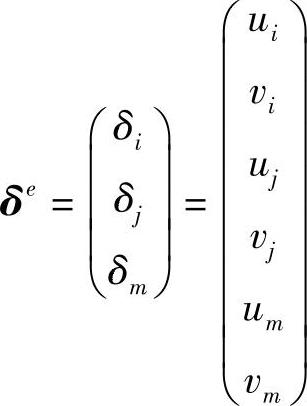

单元内的位移函数可以简写成，

f=Nδ^e （3-14）

把N称为形态矩阵，N_i称为形态函数。

虽然单元位移函数是由我们设定的，但是选择单元位移函数应满足以下条件：

1）反映单元的刚体位移与常量应变，称为完备性条件。

2）相邻单元在公共边界上的位移连续，单元之间不能重叠，也不能脱离。即位移函数在单元之间连续，称为协调性条件。

单元位移函数满足以上两个条件，就满足收敛性要求。由式（3-6）可以将单元位移表示成以下的形式，(https://www.daowen.com)

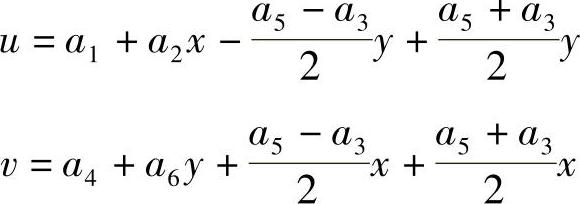
可见单元位移函数包含了刚体位移和常应变。

单元位移函数是线性插值函数，因此单元边界上各点的位移可以由两个结点的位移完全确定。两个单元的边界共用两个结点，所以边界上的位移连续。

形态函数N_i具有以下性质：

1）在单元结点上形态函数的值为1或为0。

2）在单元中的任意一点上，三个形态函数之和等于1。

用行列式T来计算三角形面积时，要注意单元结点的排列顺序，当三个结点i，j，m取逆时针顺序时，A=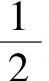T＞0；当三个结点i，j，m取顺时针顺序时，A=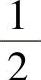T＜0。

三角形单元的形态函数N_i具有明确的几何意义，如图3-17所示。

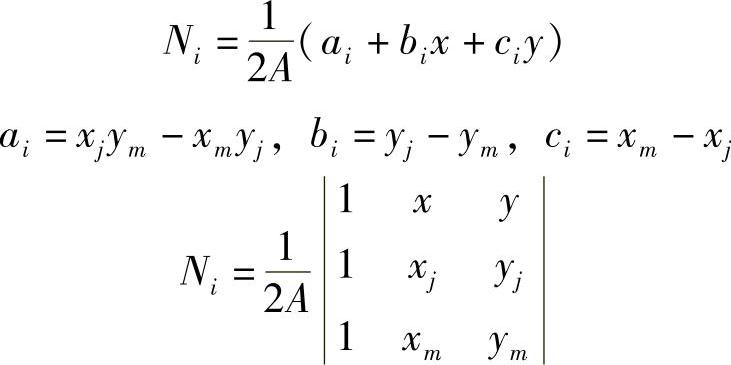
P点的坐标为（x，y），则矩阵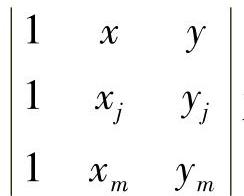为三角形PIJ面积的两倍，因此形态函数N_i=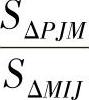，N_i为三角形面积之比。同样，，

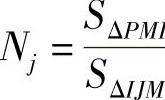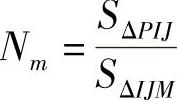
例3-1：等腰三角形单元如图3-18所示，求其形态矩阵[N]。

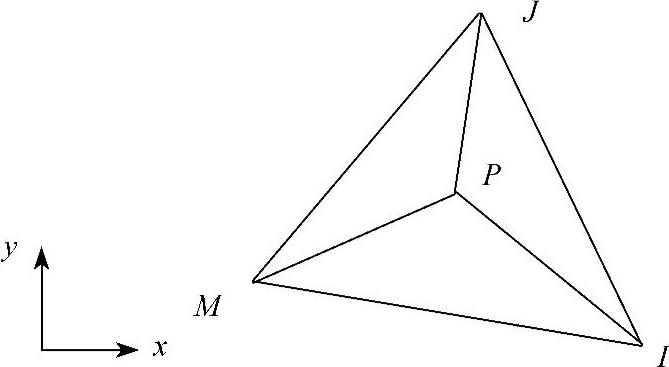
图3-17 三角形单元形态函数几何意义

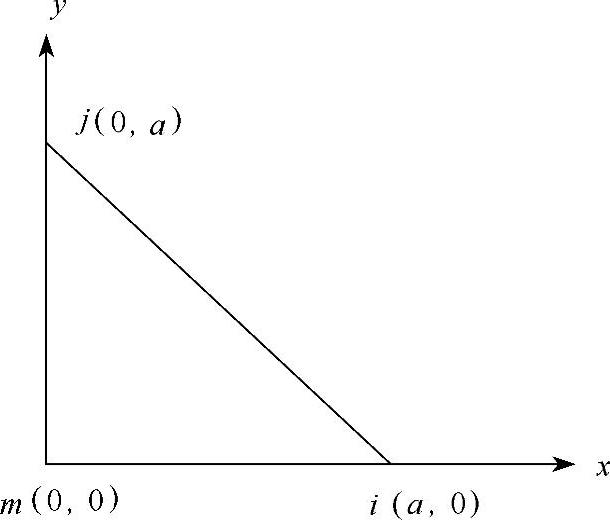
图3-18 三角形单元

解：由a_i=x_jy_m-x_my_j，b_i=y_j-y_m，c_i=x_m-x_j

在公式中轮换下标可以计算得

a_i=x_jy_m-x_my_j=0×0-0×a=0，b_i=y_j-y_m=a-0=a，

c_i=x_m-x_j=0-0；

a_j=x_my_i-x_iy_m=0×0-a×0=0，b_j=y_m-y_i=0-0=0，

c_j=x_i-x_m=a-0=a；

a_m=x_iy_j-x_jy_i=a×a-0×0=a²，

b_m=y_i-y_j=0-a=-a，c_m=x_j-x_i=0-a=-a

三角形积为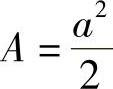

形态函数为，

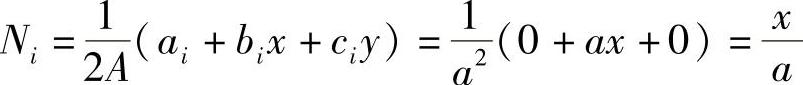
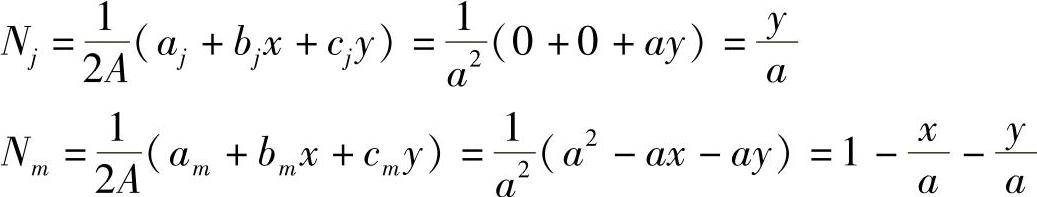
根据形态函数的几何意义，可以直接得到上面的结果。

形态矩阵为，

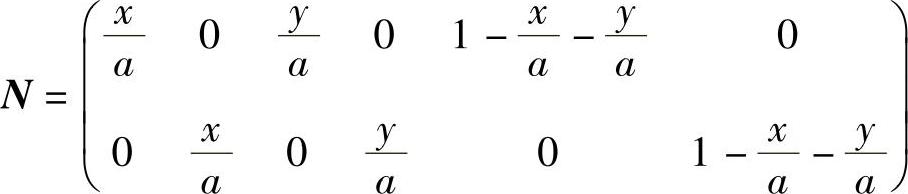
三角形面积的计算公式可得，

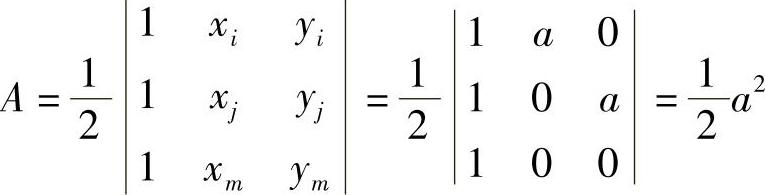
如果把三个结点按顺时针方向排列，即i（a，0），j（0，0），m（0，a）

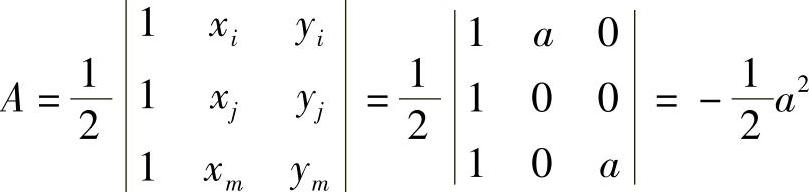
例3-2：三结点三角形单元如图3-19所示。结点位移如下：u_i=0.1a，v_i=0.05a，u_j=0.15a，v_j=0.1a，u_m=0.05a，v_m=0。单元内一点P的坐标为（0.25a，0.5a），求P点的位移。

解：由单元位移函数，f（P）=N（P）δ^e

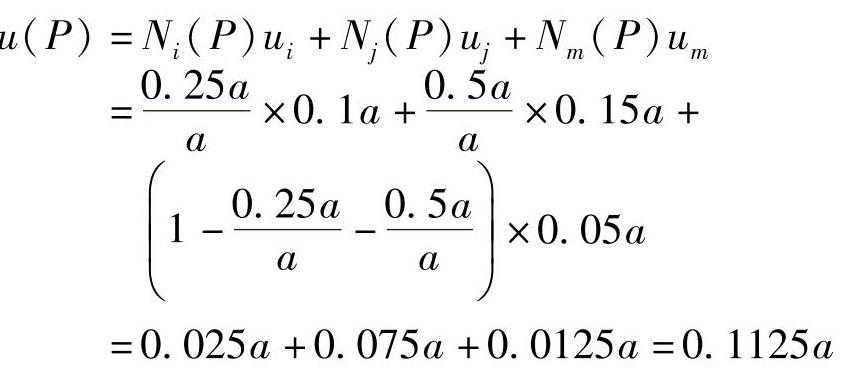
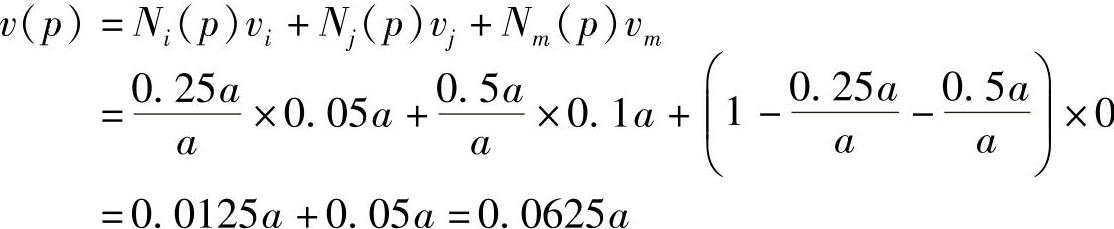
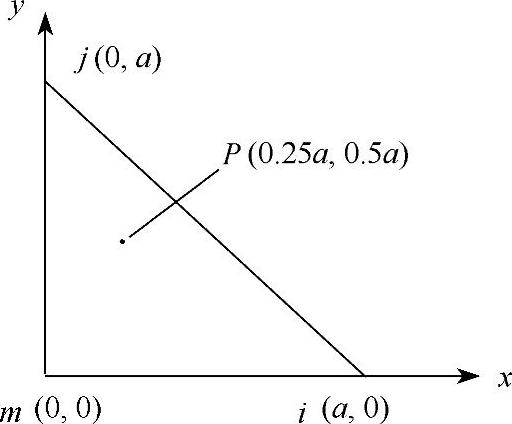
图3-19 三角形单元中一点的位移

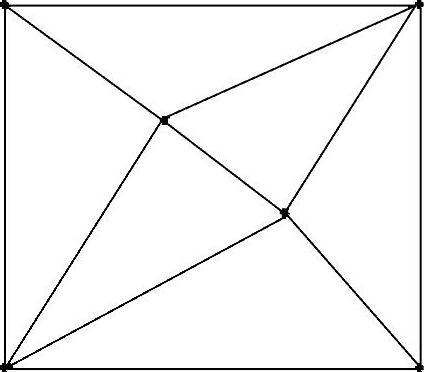
图3-20 小块检验示意图

单元的位移模式是否满足收敛性要求，可以通过一种称为小块检验的方法来检验。分片检验由B·M·Irons首先提出，已经证明分片检验给出了收敛性的充分条件。基本方法如下：取几个单元拼装的一个小块弹性体，单元的划分方式要确保至少使一个结点完全被单元包围，即内部结点。可以改变内部结点的位置，使单元具有任意形状，如图3-20所示。把与常应变状态协调的位移或外力施加到边界结点上，内部结点不受外力作用，也没有位移约束。如果计算出的单元位移、应力和应变，与给定的常应变状态一致，则称该位移模式通过了小块检验，满足收敛性。