物体中某一点的位移可以直接度量，物体的变形可以用位移来表示，几何方程表示位移和变形之间的关系。对于平面问题，在物体内的任意一点P有通过该点的两个相互垂直的微小线段PA和PB，PA平行于X轴，PB平行于Y轴，根据图3-12所给出的位移形式可以得到位移和应变分量的关系。

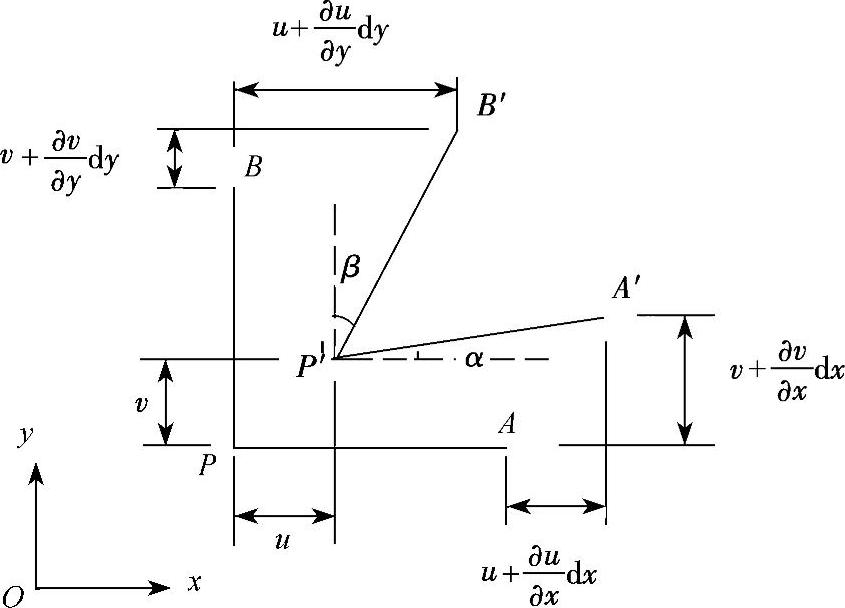
图3-12 位移与变形关系示意

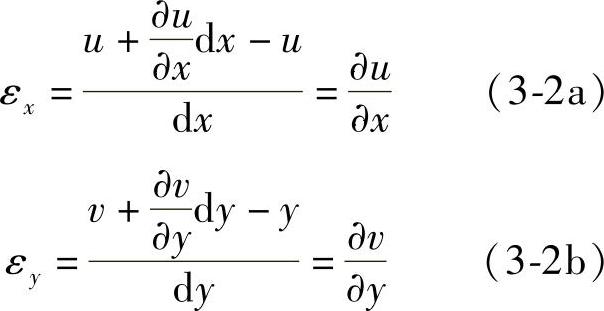
在小变形的情况下，

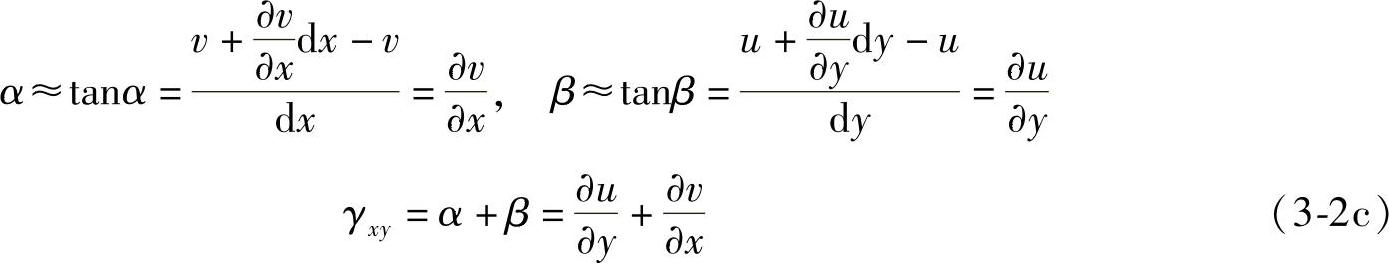
由位移分量u=0、v=0可以得到应变分量为零，反过来，应变分量为零则位移分量不为零。应变分量为零时的位移称为刚体位移。刚体位移代表了物体在平面内的移动和转动。

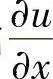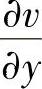由=0，=0可得，

u=f₁（y），v=f₂（x）

将f₁，f₂代入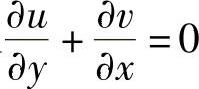可得，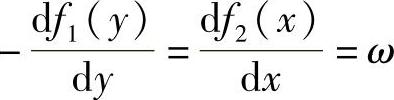

积分后得到，

f₁（y）=u₀-ω_y

f₂（x）=v₀+ω_x(www.daowen.com)

得到位移分量，

u=u₀-ω_y

v=v₀+ω_x

当u₀≠0，v₀=0，ω=0时，物体内任意一点都沿x方向移动相同的距离，可见u₀代表物体在x方向上的刚体平移。

当u₀=0，v₀≠0，ω=0时，物体内任意一点都沿y方向移动相同的距离，可见v₀代表物体在y方向上的刚体平移。

当u₀=0，v₀=0，ω≠0时，可以假定ω＞0，如图3-13所示，此时的物体内任意一点P（x，y）的位移分量为u=-ω_y，v=ω_x。

合成位移为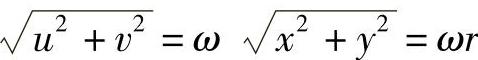，，式中，r是P点到z轴的距离。

设合成位移与y轴的夹角为α，径向线PO与x轴的夹角为θ，

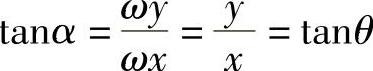
合成位移的方向与径向线PO垂直，大小与PO的距离成正比，可见ω代表物体绕z轴的刚体转动。

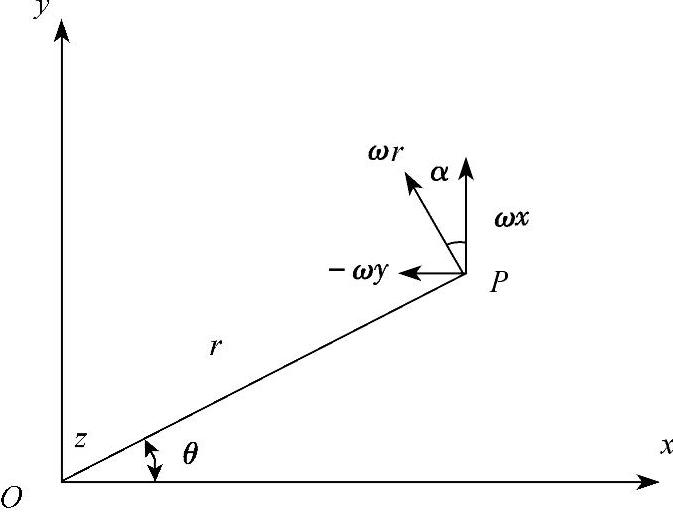
图3-13 刚体位移的物理意义