弹性体在满足一定条件时，其变形和应力的分布规律可以用在某一平面内的变形和应力的分布规律来代替，这类问题称为平面问题。平面问题分为平面应力问题和平面应变问题。

1.平面应力问题

设有很薄的等厚薄板，只在板边上受到平行于板面并且不沿厚度变化的面力，体力也平行于板面且不沿厚度变化，如图3-8所示。

设板的厚度为t，在板面上：

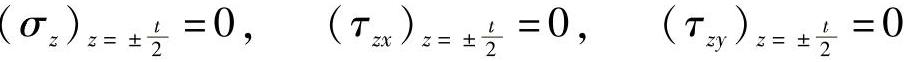
由于平板很薄，而且外力不沿厚度变化，因此在整块板上有，

σ_z=0，τ_zx=0，τ_zy=0

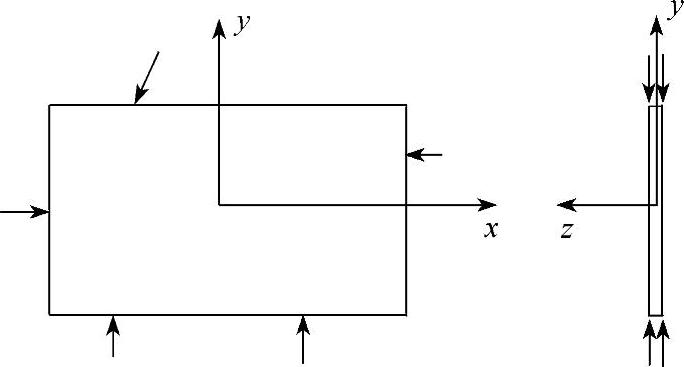
图3-8 平面应力问题示意

剩下平行于xy平面的三个应力分量σ_x、σ_y、τ_xy未知，这三个应力分量都是坐标x、y的函数。

2.平面应变问题

设有很长的柱形体，支承情况不沿长度变化，在柱面上受到平行于横截面而且不沿长度变化的面力，体力也如此分布。埋在地下的管道，挡土墙或水坝就很接近平面应变问题，如图3-9和图3-10所示。

以柱体的任一横截面为xy平面，任一垂直于横截面的纵线为z轴。假定该柱体为无限长，则任一截面都可以看作对称面。根据变形的对称性可得，(www.daowen.com)

τ_zx=0，τ_zy=0，w=0

由于没有z方向的位移，z方向的应变ε_z=0。物体在z方向处于自平衡状态，应力分量σ_z不为零，但可以不考虑。

未知量为平行于xy平面的三个应力分量σ_x、σ_y、τ_xy，这三个应力分量都是坐标x、y的函数。

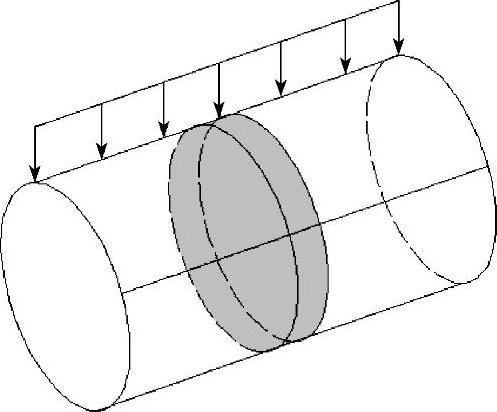
图3-9 平面应变问题示意

图3-10 挡水坝

对弹性力学平面问题的特点总结如下：

1）可以把弹性体中的某个平面定义为xy平面。弹性体内所有应力和应变分量都只是坐标x、y的函数与坐标z无关。只需要了解弹性体在该平面内的变形和受力特征，就可以了解整个弹性体的变形和受力特征。

2）所有外力和约束均平行于xy平面，只存在面内位移，没有z方向的位移。即只存在面内的位移，没有面外的位移。以很薄的平板为例，如果受到垂直与板面的作用力，平板会产生垂直于板面的位移，就不构成平面问题。

3）平面应力问题在z方向的尺寸很小，z方向应变不为零，z方向应力为零。

4）平面应变问题在z方向的尺寸很大，z方向应变为零；z方向应力不为零，存在自平衡的正应力。