弹性力学中的基本变量为体力、面力、应力、位移、应变。
体力是分布在物体体积内的力,例如重力和惯性力。面力是分布在物体表面上的力,例如接触压力、流体压力。
位移就是位置的移动。物体内任意一点的位移,用位移在x,y,z坐标轴上的投影u、v、w表示。
物体受到约束和外力作用,其内部将产生内力。物体内某一点的内力就是应力。
如图3-1所示,假想用通过物体内任意一点P的一个截面mn将物理分为Ⅰ、Ⅱ两部分。将部分Ⅱ撇开,根据内力平衡原则,部分Ⅱ将在截面mn上作用一定的内力。在mn截面上取包含P点的微小面积ΔA,作用于ΔA面积上的内力为ΔQ。令ΔA无限减小而趋于P点时,ΔQ的极限S就是物体在P点的应力。
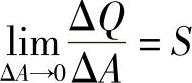
弹性力学问题满足连续性假定,因此可以计算极限。应力S可以按照不同的方向分解成分量,例如按照坐标轴的方向进行分解,其中最重要的分解方式是按照截面的外法线方向进行分解。应力S在其作用截面上的法向分量称为正应力,用σ表示;在作用截面上的切向分量称为剪应力,用τ表示。正应力和剪应力可以与材料强度相关联。
显然,如果通过P点的截面方向不同,P点在不同截面上的应力是不同的。以图3-2的等截面直杆为例,根据不同的截面方向可以得到不同的应力分量数值。为分析P点的应力状态,即通过P点的任意截面上的应力分量的大小和方向,在P点附近取出一个平行六面体,六面体的各棱边平行于坐标轴,如图3-3所示。将每个面上的应力分解为一个正应力和两个剪应力,分别与三个坐标轴平行。用六面体表面的应力分量来表示P点的应力状态。
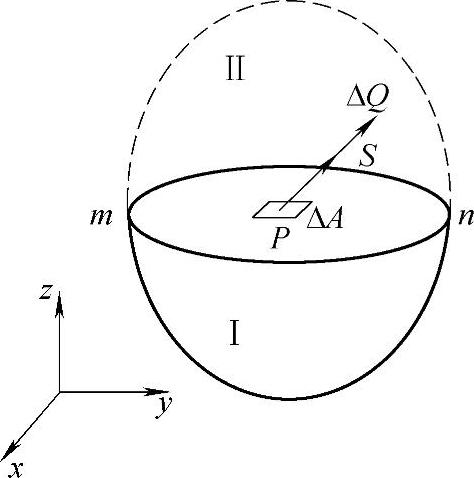
图3-1 应力定义
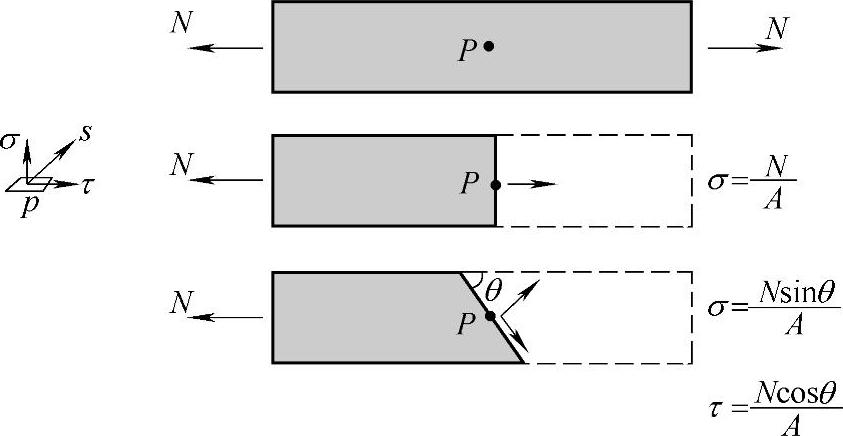
图3-2 不同方向截面上的应力分量
剪应力互等:τxy=τyx,τyz=τzy,τzx=τxz
物体内任意一点的应力状态可以用六个独立的应力分量σx、σy、σz、τxy、τyz、τzx来表示,如图3-3所示。
应力分量的下标约定如下:
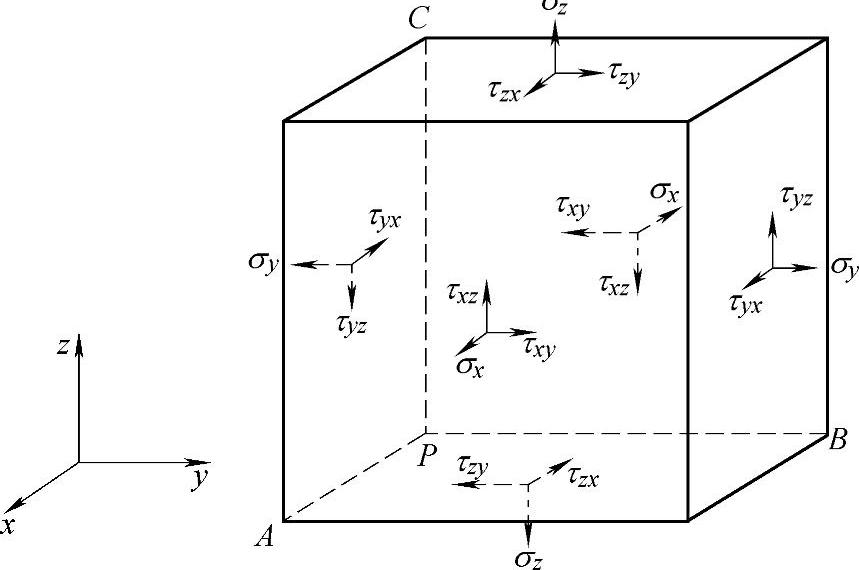
图3-3 六面体上的应力分量
第一个下标表示应力分量的作用面的法线方向,第二个下标表示应力分量的作用方向。例如τxy,第一个下标x表示剪应力作用在垂直于x轴的面上,第二个下标y表示剪应力指向y轴方向。正应力由于作用表面与作用方向垂直,使用一个下标。例如,σx表示的正应力作用于垂直于x轴的面上,指向x轴方向。
应力分量正负符号的约定如下:
如果某截面上的外法线是沿坐标轴的正方向,这个截面上的应力分量以沿坐标轴正方向为正;如果某截面上的外法线是沿坐标轴的负方向,这个截面上的应力分量以沿坐标轴负方向为正。
如图3-3所示,立方体顶面的外法线方向指向z轴的正方向,在顶面上的三个应力分量也都指向坐标轴的正方向。立方体底面的外法线方向指向z轴的负方向,在底面上的三个应力分量也都指向坐标轴的负方向。
如图3-4所示,用六个应力分量可以表示经过P点的任意斜面上的应力。
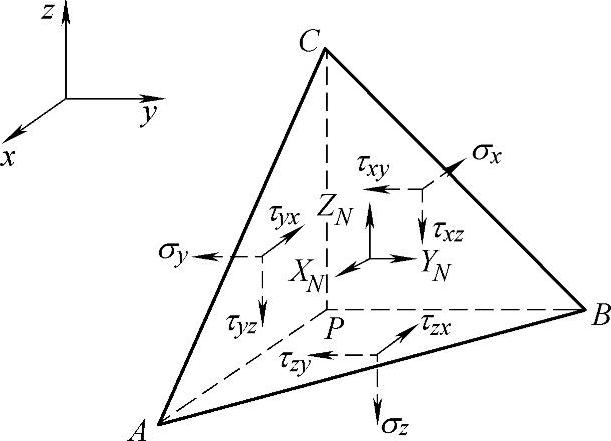
图3-4 任意斜面上的应力
根据力的平衡,可以到斜面上面力沿三个坐标轴的分量,
XN=lσx+mτyx+nτzx(https://www.daowen.com)
YN=mσy+nτzy+lτxy
ZN=nσz+lτxy+mτyz
其中,l,m,n为斜面外法线方向的三个方向余弦,即斜面外法线方向与坐标轴正方向的夹角的余弦,
l=cos(N,X),m=cos(N,X),n=cos(N,Z)
再利用力的平衡关系可以方便地求出斜面上的正应力,
σNΔS=XNΔSl+YNΔSm+ZNΔSn
σN=l2σx+m2σy+n2σz+2mnτyz+2nlτzx+2lmτxy
注意:在上面公式中,应力分量之间不存在平衡关系,而是力之间存在平衡关系。应力分量乘上其作用的面积就得到力。
物体内一点的应力分量数值与坐标系的方向相关,但是该点的三个主应力值不变。直观地理解就是应力分量随坐标系的定义方式而变化,但是物体内某一点的真实应力状态应该不随坐标系变化。那么一点的应力大小或应力强度应该如何表示?显然不能用应力分量来表示,也不能用某个主应力表示。可以用等效应力(Equivalent stress)表示物体内某个点的应力大小。用应力分量把等效应力定义为,
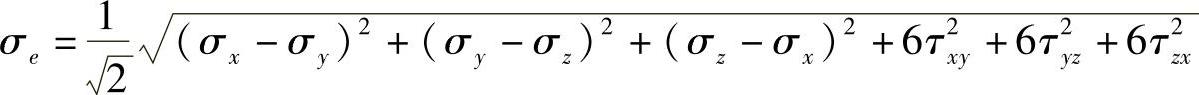
用三个主应力分量把等效应力定义为,
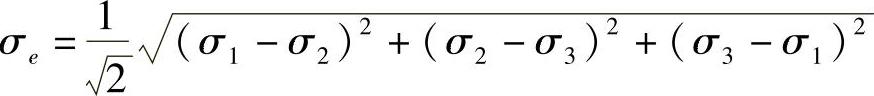
等效应力与材料力学课程中所讨论的第四强度理论是一致的,具有相应的物理意义。按照等效应力的定义,可以用一个相同的指标对比图3-5所示的不同应力状态。
单向拉伸应力状态,σ1>0,σ2=σ3=0,σe=σ1
单向压缩状态,σ3<0,σ1=σ2=0,σe=-σ3
纯剪切状态,σ3=-τ,σ2=0,σ1=τ,σe=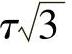 物体的形状改变可以归结为长度和角度的改变。应变可以理解为相对变形,无量纲。如图3-6所示,线段的单位长度的伸缩,称为正应变,用ε表示。两个垂直线段之间的直角的改变,用弧度表示,称为剪应变,用γ表示。
物体的形状改变可以归结为长度和角度的改变。应变可以理解为相对变形,无量纲。如图3-6所示,线段的单位长度的伸缩,称为正应变,用ε表示。两个垂直线段之间的直角的改变,用弧度表示,称为剪应变,用γ表示。
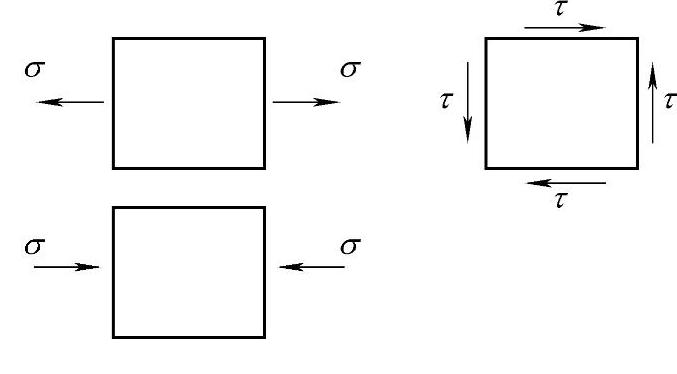
图3-5 不同应力状态的对比
与应力定义类似,为定义物体内任意一点P的变形,在P点沿坐标轴方向取三个微小线段PA、PB、PC。与应力的定义类似,物体内任意一点的变形,可以用六个应变分量表示,
εx、εy、εz、γxy、γyz、γzx
εx为线段PA的正应变,εy为线段PB的正应变,εz为线段PC的正应变,γxy为线段PA、PB夹角的改变,γyz为线段PB、PC夹角的改变,γzx为线段PC、PA夹角的改变,如图3-7所示。
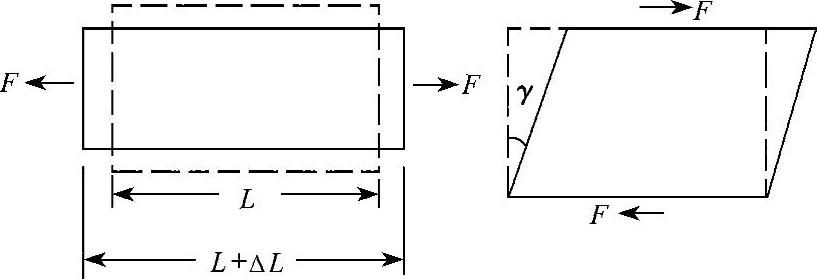
图3-6 应变的定义方法
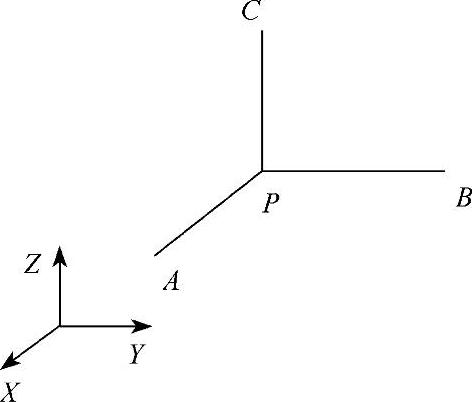
图3-7 任意一点的应变状态
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






