平面桁架的整体分析-有限元分析基础与应用教程

平面桁架结点的总体自由度编号与单元结点的局部自由度编号如表1-2所示。

表1-2 平面桁架结点的总体自由度编号与单元结点的局部自由度编号

根据单元结点的局部编号与结点的总体自由度编号的关系，把单元刚度矩阵直接叠加得到总体刚度矩阵，即整个结构所受的外部载荷由全部单元来分担。例如，单元1的局部自由度1、2，单元3的局部自由度1、2，都对应为整体自由度1、2，那么把两个单元刚度矩阵对应的系数相叠加。

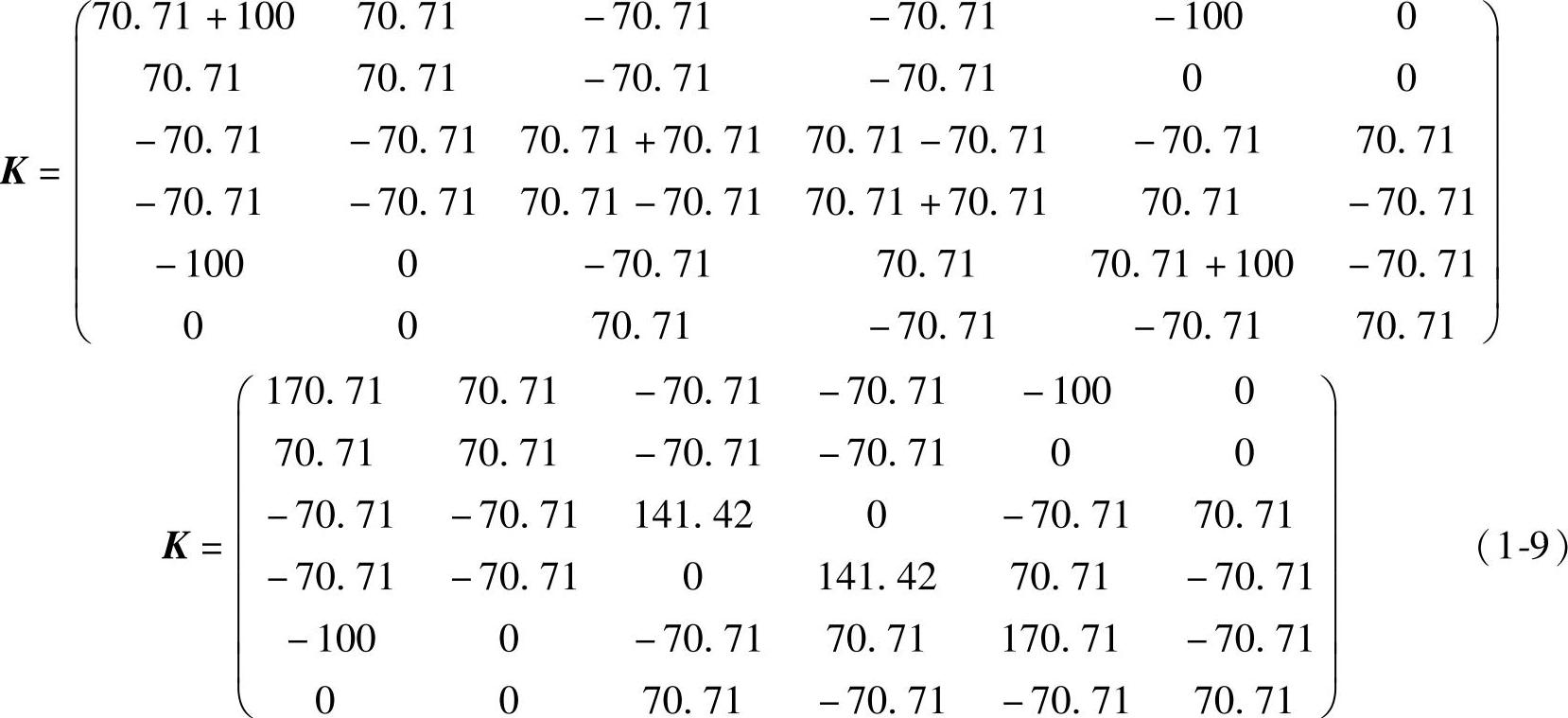
根据位移边界条件，U₁=V₁=V₃=0。在总体刚度矩阵中去掉与零位移对应的行与列，得到式（1-10）：

则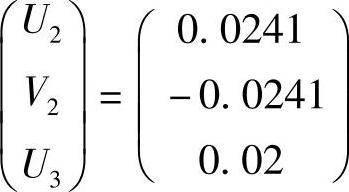

单元的内力按以下公式计算：

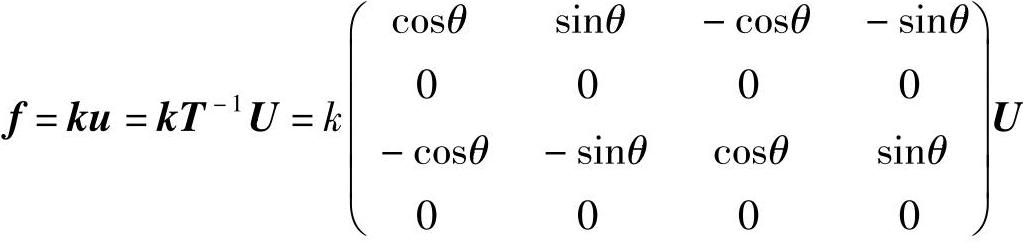
单元1的内力为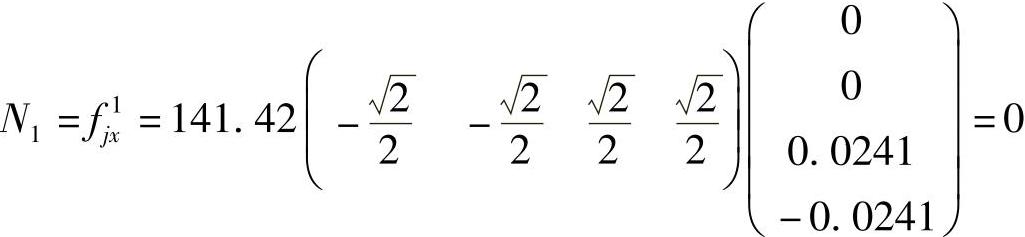

单元2的内力为

单元3的内力为

下面用在自重作用下的等截面直杆来说明求解连续问题的有限单元法的原理。受自重作用的等截面直杆如图1-11所示，杆的长度为L，截面积为A，弹性模量为E，单位长度的重量为q，杆的内力为N。试求：杆的位移分布，杆沿轴向的应变和横截面上的正应力。

（1）等截面直杆在自重作用下的材料力学解答

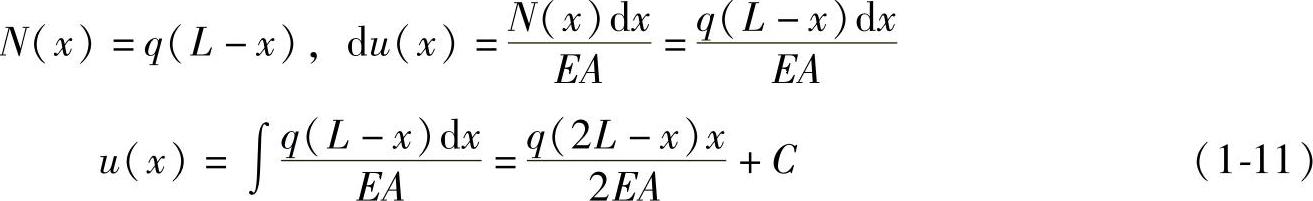
当x=0时，u（0）=0

所以，，，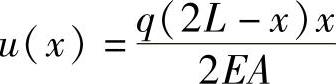

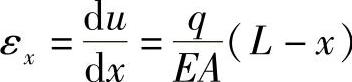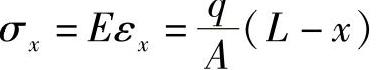
（2）等截面直杆在自重作用下的有限单元法解答

1）离散化。如图1-12所示，将直杆划分成n个有限分段，有限分段之间通过一个铰接点连接。称两分段之间的铰接点为结点，称每个有限分段为单元。其中，第i个单元的长度为L_i。包含第i，i+1个结点。

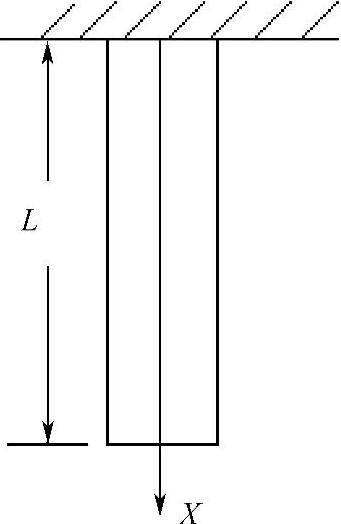
图1-11 受自重作用的等截面直杆

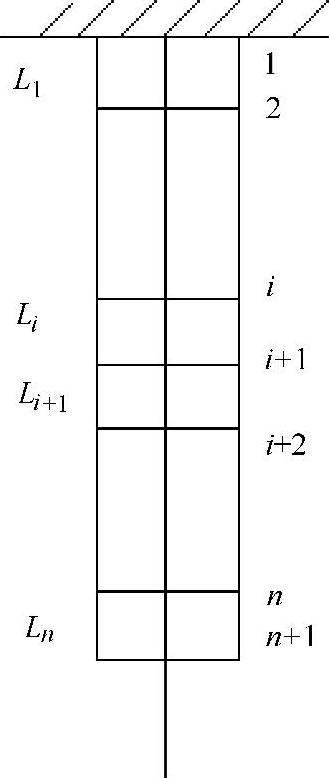
图1-12 离散后的直杆

2）用单元结点位移表示单元内部位移。第i个单元中的位移分布用所包含的结点位移来表示，

式中，u_i是第i结点的位移；x_i是第i结点的坐标。

第i个单元的应变为ε_i，应力为σ_i，内力为N_i(https://www.daowen.com)

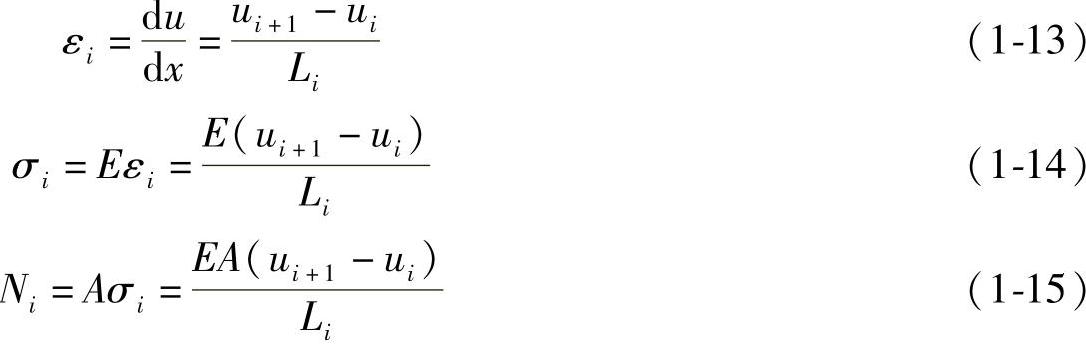
由于单元内部的位移分布被假设成为结点位移的线性插值，单元内的应变、应力和内力都是常数。

3）把外载荷集中到结点上。如图1-13所示，把第i单元和第i+1单元重量的一半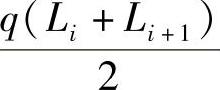，集中到第i+1结点上。这样处理的原因是，集中在结点上的外载荷与单元上的分布载荷要满足静力等效。

4）建立结点的力平衡方程。对于第i+1结点，由力的平衡方程可得：

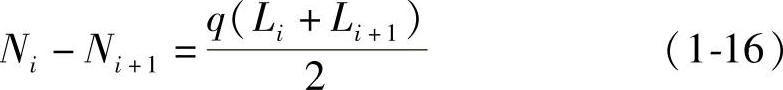
令，并将式（1-15）代入得：

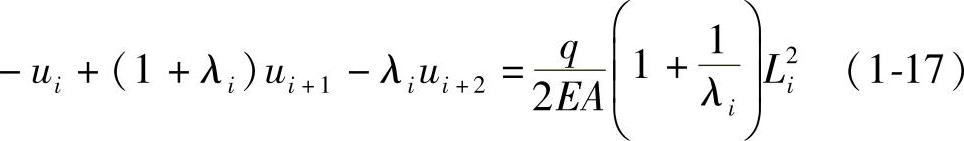
对于第n+1个结点，平衡方程为：

根据约束条件，u₁=0。建立所有结点的力平衡方程，可以得到由n+1个方程构成的方程组，可解出n+1个未知的结点位移。

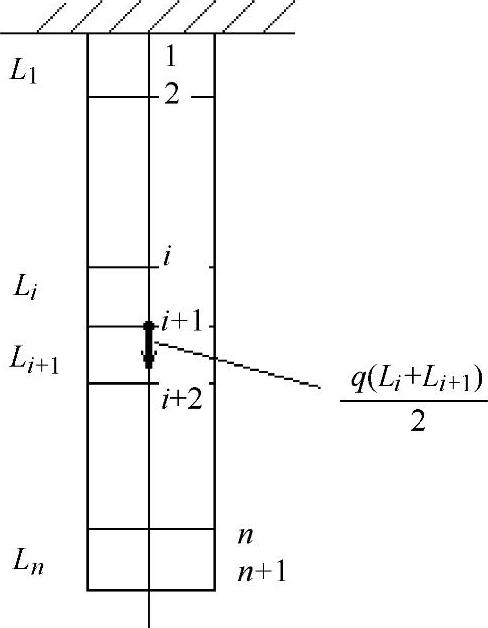
图1-13 单元外载荷的移置

例1-2：将受自重作用的等截面直杆划分成如图1-14所示的3个等长的单元，试求杆的位移。

定义单元的长度为。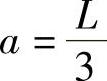

对于结点1，u₁=0

对于结点2，由式（1-17）可得，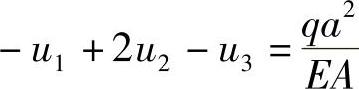

同样，对于结点3有，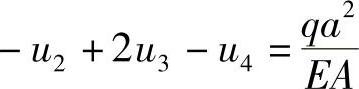

对于结点4，可以有两种处理方法。

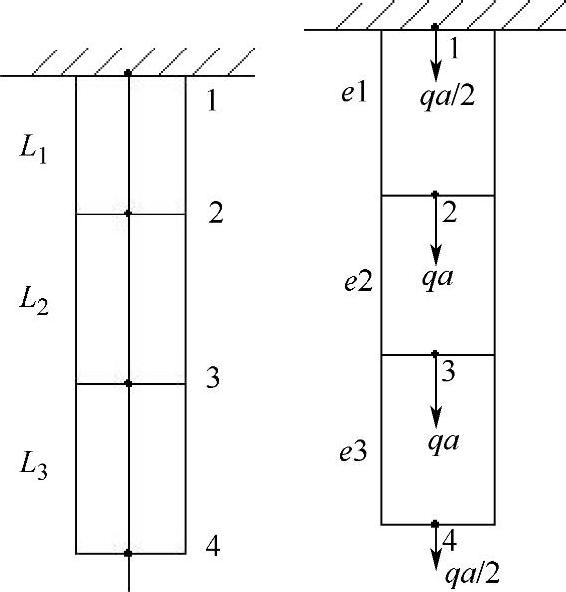
图1-14 离散为3个单元后的直杆

1）直接用第3个单元的内力与结点4上的载荷建立平衡方程

，，

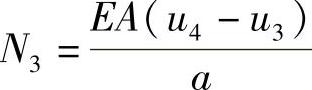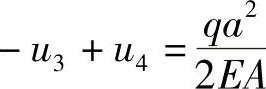
2）假定存在一个虚拟结点5，与结点4构成了虚拟单元4

在结点4上应用式（1-17），

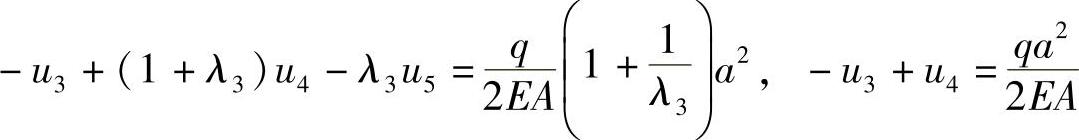
整理后得到线性方程组，，解得