【摘要】:1)在局部坐标系中建立结点力分量与结点位移分量的关系矩阵。f=T-1F=ku=kT-1U在整体坐标系中,单元结点力分量与位移分量的关系矩阵为:直杆的刚度EA=10000kN。图1-10 单元局部坐标与整体坐标的关系单元2局部坐标与整体坐标的关系如图1-10b所示,θ=-45°。
1)在局部坐标系中建立结点力分量与结点位移分量的关系矩阵。局部坐标系x轴的正方向由首结点i指向尾结点j,结点位移与结点力如图1-8所示。

图1-8 直杆的结点位移与结点力
根据胡克定律
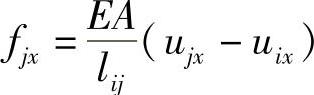
由单元平衡,得fix=-fjx
设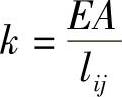 ,得到局部坐标系中结点力分量与结点位移分量之间的关系,
,得到局部坐标系中结点力分量与结点位移分量之间的关系,
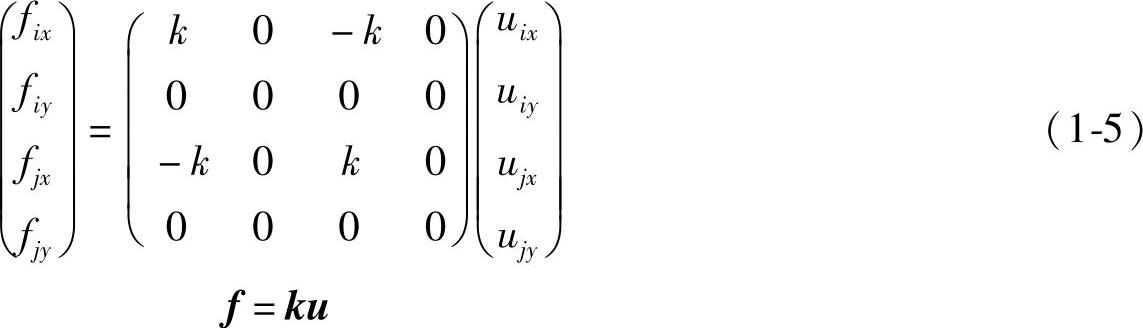
2)如图1-9所示,根据局部坐标系中结点位移、结点力分量与整体坐标系中结点位移、结点力分量之间的关系,建立转换矩阵T。得到整体坐标系下的结点力与结点位移分量。
局部坐标系相对整体坐标系的夹角为θ,夹角的正负号遵守右手法则(从X轴正向转向Y轴正向为正)。在整体坐标系中的结点位移分量与局部坐标系中的结点位移分量存在以下关系:
Uix=uixcosθ-uiysinθ
Uiy=uixsinθ+uiycosθ
写成矩阵形式,
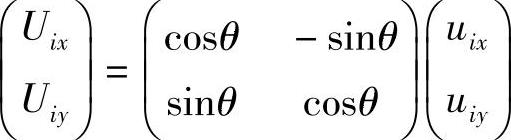
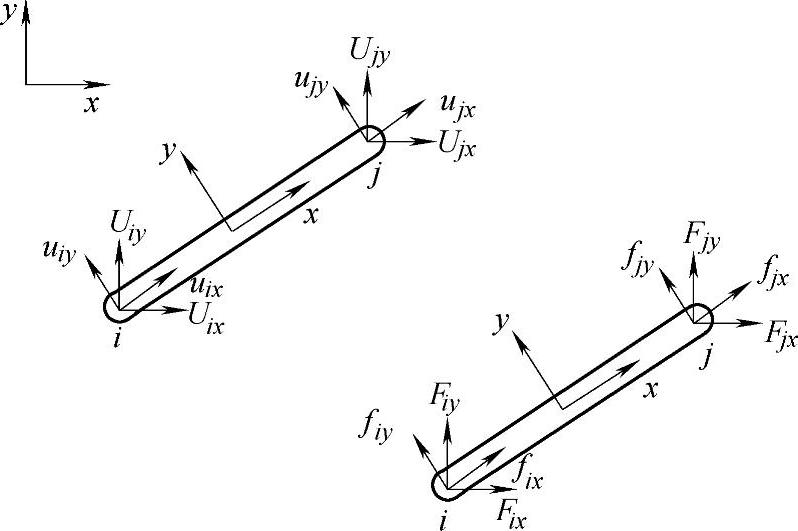
图1-9 整体坐标系与局部坐标系中的结点力与位移分量(https://www.daowen.com)
将局部坐标系中单元结点变量转换到整体坐标系中单元结点变量的转换矩阵T定义如下:
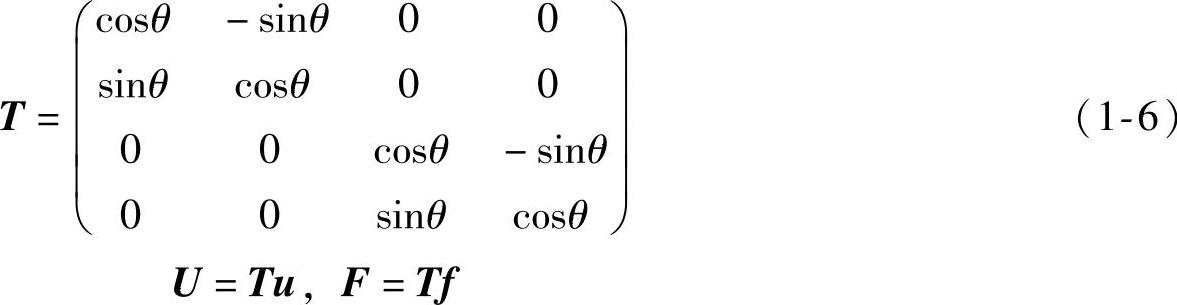
3)在整体坐标系中建立单元结点力分量与位移分量的关系矩阵。
f=T-1F=ku=kT-1U
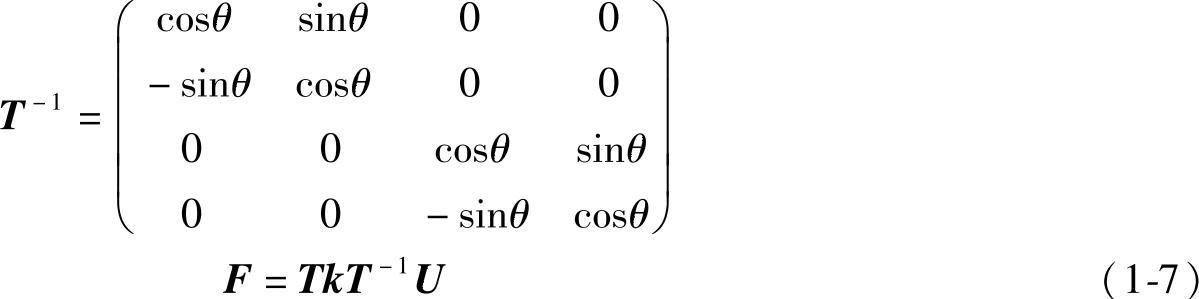
在整体坐标系中,单元结点力分量与位移分量的关系矩阵(单元刚度矩阵)为:
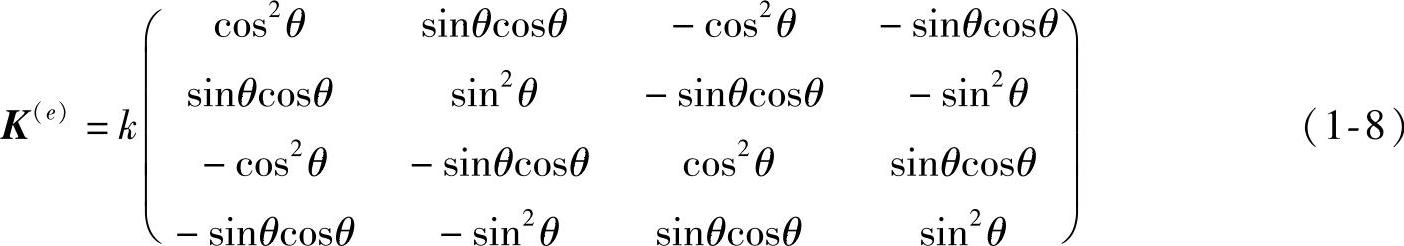
直杆的刚度EA=10000kN。
单元1局部坐标与整体坐标的关系如图1-10a所示,θ=45°。
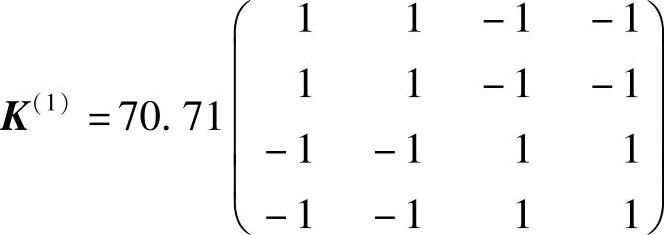
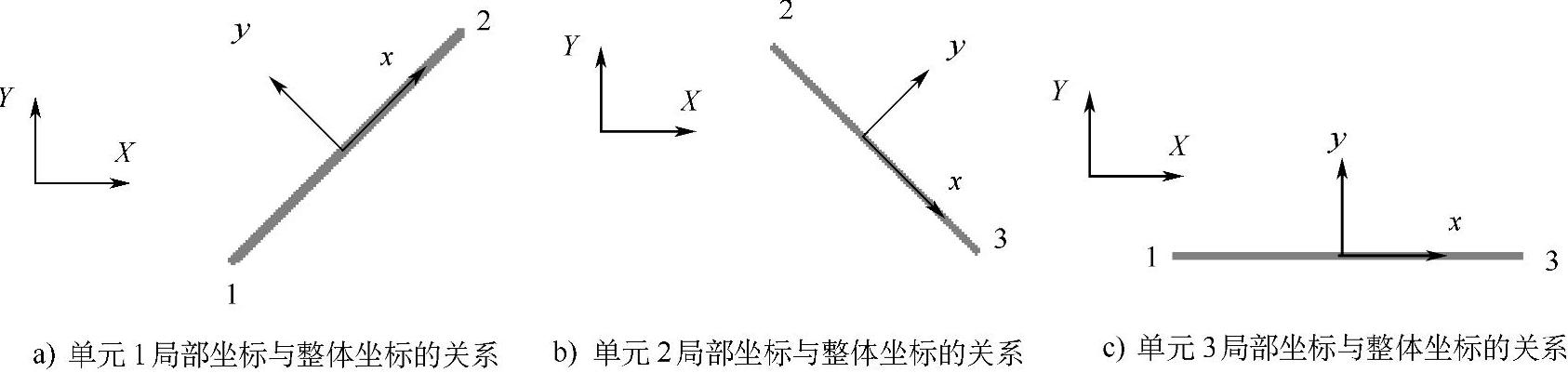
图1-10 单元局部坐标与整体坐标的关系
单元2局部坐标与整体坐标的关系如图1-10b所示,θ=-45°。单元3局部坐标与整体坐标的关系如图1-10c所示,θ=0°。
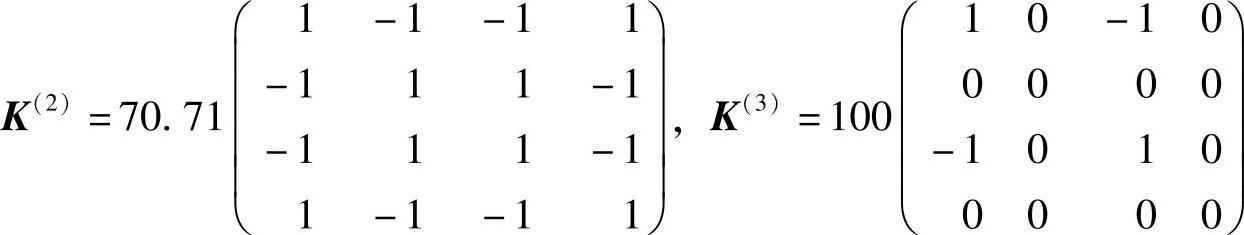
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






