在这里引用O·C·Zienkiewicz的一段话来说明有限单元法的一般原理，“人类思维的限制在于不能通过一步运算就掌握复杂环境和事物的行为。因此，先把所有系统分解为它们的元件或单元，这些元件的行为已经被充分地了解，再把元件重新组装成原来的系统来研究系统的行为。这种研究方法是一种很自然的方法，工程师、科学家，甚至经济学家都在使用。”

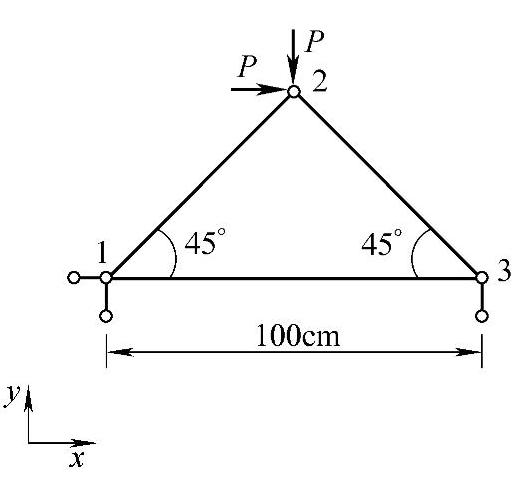
图1-7 平面桁架

例1-1：平面桁架123如图1-7所示。已知各杆件的弹性模量E=2.0×10⁵MPa，各杆的截面积均为A=0.5cm²，杆13的长度为100cm，载荷P=2kN。求平面桁架各杆的内力与位移。

假设杆12、杆23和杆13的内力分别为N₁、N₂和N₃。

结点2在X方向和Y方向的平衡方程分别为

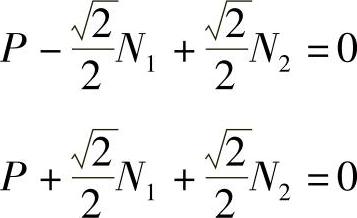(www.daowen.com)

由上面的两个方程可以得到，N₁=0kN，N₂=-2.828kN。结点3在X方向的平衡方程为

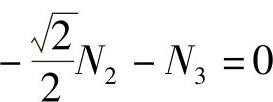
解得 N₃=2kN

如果按照上面所述思路来求解大型平面桁架，计算的工作量很大，而且不同的解题者可能采用不同的解算思路。通过分析单个杆件的受力变形特征，可以建立规则的解算方法来计算平面桁架的受力，并用计算机实现这种解算方法。平面桁架属于离散结构系统，各杆件自然就是单元。杆12为单元1，杆23为单元2，杆13为单元3。单元编号、结点编号与单元长度如表1-1所示。

表1-1 单元编号、结点编号与单元长度