在科学研究或解决工程技术问题的时候，通常会根据观测、实验的结果来研究基本元素的性质、规律，建立基本元素的数学模型。再把基本元素组合成实际研究对象，建立实际研究对象的数学模型，最后求解这个数学模型。在科学研究和工程技术领域内，经常会遇到两类典型的问题。第一类问题可以归结为有限个已知基本元素的组合。例如，材料力学中的连续梁、建筑结构框架和桁架结构。这类问题称为离散问题。

如图1-1所示平面桁架结构，是由5根只承受轴向力的直杆组成，其中每根直杆的受力状况相同，桁架结构的基本元素自然是直杆。图1-2是北京故宫太和殿，建筑主体是木质梁架结构，其中每根梁、立柱可以作为一个基本元素。图1-3是法国巴黎的埃菲尔铁塔，塔身全是钢架镂空结构，用1.8万余个金属部件安装而成，高300.65m，重达7000t，于1889年竣工。图1-4是国家体育场的外观。尽管像埃菲尔铁塔、国家体育场这类现代建筑的结构非常复杂，还是由一些基本构件组成。国家体育场外壳就是由图1-5所示的支架组成。

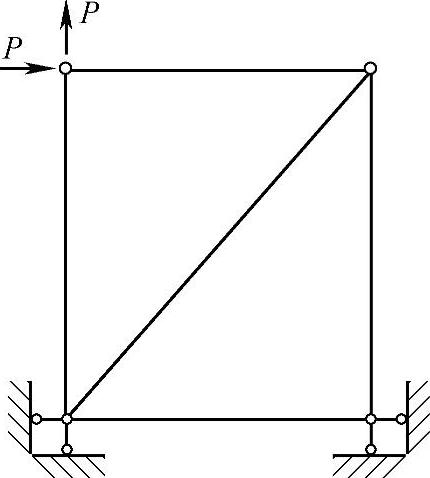
图1-1 平面桁架系统

图1-2 北京故宫太和殿

图1-3 巴黎埃菲尔铁塔

图1-4 国家体育场外观

图1-5 国家体育场外壳的支架

这类离散问题的特点是：①可以把整个对象分解为有限个相同或相似的基本元素；②用相同的方法分析每个组成元素；③不管规模有多大，离散问题是可解的。特别是随着计算机技术的发展，已经能够求解图1-3、图1-4这样结构复杂、规模巨大的离散问题。

第二类问题是针对连续介质，通常可以建立这些问题应遵循的基本方程，即微分方程和相应的边界条件。与离散问题不同，在建立基本方程时所研究的对象通常是无限小的单元，所以这类问题称为连续体问题，例如热传导问题，弹性力学问题，电磁场问题等。(www.daowen.com)

以三维空间均匀连续介质中的热传导问题为例，这个问题可以归结为由控制方程、初始条件与换热边界条件所组成的方程组：

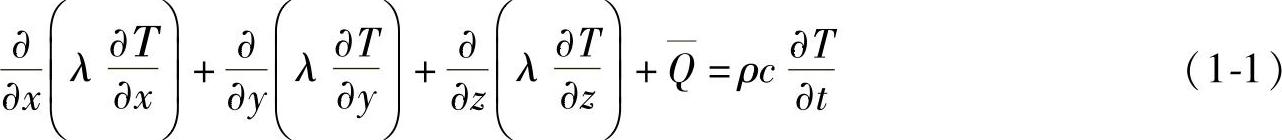
式中，T为温度；x、y、z是空间坐标；t是时间；λ是导热系数；ρ是材料密度；c是比热容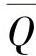；是内部热源。

初始温度场可以是不均匀的，但各点温度值都是已知的，其函数表达为：

有三种换热边界，其中第三类换热边界条件为：

有关热传导问题的偏微分方程组是封闭的，因此可以用解析方法求解。但是对于许多复杂的热传导问题，无法得到解析解。

尽管已经建立了连续介质问题的基本方程，由于边界条件的限制，通常只能得到少数简单问题的解析解，对于许多实际的工程问题还无法给出解析解。为解决这个困难，工程师们和数学家们提出了许多近似方法。

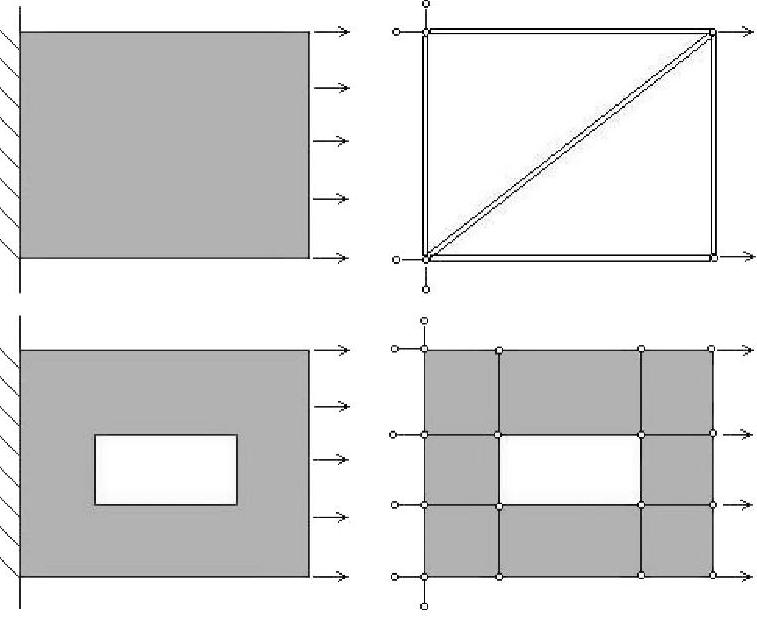
图1-6 连续体与离散结构的比拟

在寻找复杂连续介质问题求解方法的过程中，工程师和数学家从两个不同的路线得到了相同的结果，即有限单元法（Finite Element Meth-od）。有限单元法的形成可以追溯到20世纪50年代甚至更早些时间，基本思路来源于固体力学中矩阵位移法的发展和工程师对结构相似性的直觉判断。对不同结构的杆系、不同的载荷，用矩阵位移法求解都可以得到统一的矩阵公式。如图1-6所示，从固体力学的角度来看，在一定的受力和约束条件下桁架结构的变形方式与连续的方板的变形方式之间存在一定的相似性，复杂形状的板可以等价为通过结点连接的多个矩形板或三角形板。这就产生了一个来自结构类比的想法，即可以把矩阵结构法的求解原理推广到非杆系结构问题的求解。

在1952～1953年期间，R·W·Clough和M·J·Turner在分析飞机三角翼（Delta Wing）振动问题时，提出了把平面应力三角形板或矩形板组合起来表达机翼刚度的方法，当时被称为直接刚度法。1956年M·J·Turner，R·W·Clough，H·C·Martin，L·J·Topp在纽约举行的航空学会年会上发表论文《复杂结构的刚度和变形分析》（“Stiffness and deflection anal-ysis of complex structures”）介绍了这种新的计算方法，从而将矩阵位移法推广到求解弹性力学平面应力问题。他们把平面板壳结构划分成一个个三角形和矩形的“单元”，利用单元中近似位移函数，求得单元结点力与结点位移关系的单元刚度矩阵。1960年，R·W·Clough在论文《平面应力分析的有限元单元》（“The finite element in plane stress analysis”）中首次提出了有限单元（Finite Element）这一术语，他也因此被称为“有限单元之父”。Clough在2001年发表的回顾文章《关于有限单元法起源的思考》（“Thoughts about the origin of the finite ele-ment method”）中详细介绍了他当年提出有限单元法的过程。Clough和E·L·Wilson在他们发表的回顾文章《伯克利早期有限单元研究》（“Early finite element research at Berkeley”）中详细地介绍了有限单元法的早期研究工作。