1.信息熵

数据压缩技术的理论基础是信息论。根据信息论的原理，人们可以找到最佳数据压缩编码方法，数据压缩的理论极限是信息熵。

信息熵是如何定义的呢？在讲信息熵之前要先说明信息、信息量这两个基本概念。信息是用不确定的量度定义的，即信息被假设为由一系列的随机变量所代表，它们往往用随机出现的符号来表示。也就是说当你收到一条消息（一定内容）之前，某一事件处于不确定的状态中，当你收到消息后，解除不确定性，从而获得信息，因此去除不确定性的多少就成为信息的度量。信息量指从N个相等的可能事件中选出一个事件所需要的信息度量和含量，即辨别N个事件中的特定事件所需提问“是”或“否”的最小次数。例如：从64个数（1～64的整数）中选定某一个数，提问：“是否大于32？”，则不论回答是与否，都消去半数的可能事件，如此下去，只要问6次这类问题，就可以从64个数中选定一个数，则所需的信息量是log₂64=6（bit）。

现在可以换一种方式定义信息量，也就是信息论中信息量的定义。设从N个数中选定任一个数x_i的概率为p（x_i），假定任选一个数的概率都相等，即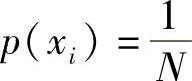，则信息量I（x_i）可定义为。

上式可随对数所用“底”的不同而取不同的值，因而其单位也就不同。设底取大于1的整数α，考虑一般物理器件的二态性，通常α=2，相应的信息量单位为比特（bit）；当α=e，相应的信息量单位为奈特（Nat）；当α=10，相应的信息量单位为哈特（Hart）。显然，当随机事件X发生的先验概率p（x）大时，算出的I（x）小，那么这个事件发生的可能性大，不确定性小，事件一旦发生后提供的信息量也少。必然事件的p（x）等于1，I（x）等于0，所以必然事件的消息报导，不含任何信息量；但是一件人们都没有估计到的事件（p（x）极小）一旦发生后，I（x）很大，即包含的信息量很大。所以随机事件的先验概率，与事件发生后所产生的信息量有密切关系。I（x）称为x发生后的自信息量，它也是一个随机变量。

下面介绍“熵”的定义。H（X）在信息论中称为信源X的“熵（Entropy）”，它的含义是信源X发出任意一个随机变量的平均信息量。

一般在解释和理解信息熵时，有4种样式：当处于事件发生之前，H（X）是不确定性的度量；当处于事件发生之时，H（X）是一种惊奇性的度量；当处于事件发生之后，H（X）是获得信息的度量；还可以理解为是事件随机性的度量。

2.编码定理(www.daowen.com)

最大离散熵定理为：所有概率分布P（x_i）所构成的熵，以等概率时为最大。另外，当P（x_i）=1时，信息熵最小，等于零。所以熵的范围如下：

0≤H（X）≤log_αN

信息熵的最大值与熵值之间的差值，就是信源X所含的冗余度（redundancy）。在编码中用熵值衡量是否为最佳编码，熵值是平均码长的下限。若用L表示编码器输出的平均码长，则：

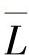>>H（X）时，有冗余，不是最佳编码；

<H（X）不可能发生，只能有≥H（X） （1-1）

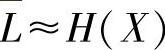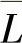（稍大于H（X））时，为最佳编码。在论述平均码长构成瞬时可解码的编码方式时，香农指出应满足

称式（3-1）和式（3-2）为香农编码定理。此编码定理给出了进行压缩编码的极限和应如何去构成压缩编码。