物体的存在导致时空的弯曲，而物体又是以质量和能量来显示自己的存在，那么质量和能量的分布就决定了时空弯曲的程度，这样两者之间可以建立一个等式关系。听起来很抽象，其实道理很简单，甲的大小决定了乙的大小，那么甲乙之间是不是就应该有一个等式关系？一个贪官的贪污受贿额度决定了他要判多少年徒刑，那么贪污受贿的额度与判刑多少年之间，是不是就可以建立一个等式？说高大一点，就是建立一个方程。

但这里需要进行一些处理，比如受贿一百万对应判刑十年，但不能说受贿一千万元就判刑一百年，这不是一个线性的关系，是非线性的。另外受贿额度与贪污额度也不能简单相加，毕竟轻重不一样；如果再考虑到有期徒刑、无期徒刑、死刑，那就更复杂了。建立一个小小的司法判刑方程都是如此的复杂，可以想见建立时空弯曲的方程该是一个什么样的难度，是一个令爱因斯坦都感到着急的难度。

好在有黎曼、里奇等一帮数学家，在不经意中事先进行了铺垫，让爱因斯坦走向了通往巅峰的路途。具体说来，就是黎曼给出了描写时空弯曲程度的概念——曲率，它是一个四阶曲率张量，过于宏大，后来里奇将之缩并，变成了二阶里奇张量，也就是说二阶的里奇张量就足以刻画时空的弯曲。

物体存在导致时空弯曲，那物体是靠什么刷存在感？是质量和能量。但此二者无法形成一个二阶张量，这就不足以与二阶的里奇张量实现对接，于是爱因斯坦进行了一番胡拼乱凑，搞出了一个二阶的能量动量张量，这样对接就成为可能。这里准备用T来表示能量动量张量，因为是二阶的，所以T应该带两个下角标。用谁当下角标？没忘吧，广相一出，μν齐上。所以就是T_μν用来表达能量动量张量。

现在我们可以说，物质的分布构成了能量动量张量T_μν，而T_μν又导致了时空弯曲，时空弯曲又可以通过里奇张量来展示。里奇张量用大写的R来表示，因为是二阶的，所以也要用两个下角标，当然也要用μ、ν，所以里奇张量就写成R_μν。

万事俱备，就差对接了，于是爱因斯坦开始行动了。我想有读者也开始对接了，不就是让里奇张量R等于能量动量张量T吗？这临门一脚的事儿，谁不会干？最多配上一个比例常数K。

是的，爱因斯坦当时也是这样想的，于是就有：

R_μν＝KT_μν

等式中的R_μν就是里奇张量，T_μν就是能量动量张量。K是比例系数，其实习惯上用的是希腊字母κ（kappa），因为长得非常像英文字母K，咱们干脆就说K，不说卡帕。

我再说一遍爱因斯坦对接出来的方程：

R_μν＝KT_μν

这就成功了？爱因斯坦内心狂喜不止。但通过仔细考察发现，这个方程的形式还是要依赖于坐标系的选择，并没有达到爱因斯坦最初的目标，即找到在所有参照系下都完全一样的数学方程形式。

爱因斯坦有点崩溃，他似乎觉得在黎曼几何中，或许就不存在他想要的那个玩意儿，但是他自己又搞不出来自己想要的东西。又折腾了一阵子，他妥协了，只好把现有的成果发表了。而且就用这个成果，他较好地计算出了水星近动，战胜了牛顿的万有引力定律。

如果是一般人，也就到此为止了，人生如此，夫复何求啊。但爱因斯坦不忘初心，他要建立一个不依赖于任何坐标系、任何参照系的数学方程。因为他坚信：真正的物理学定律一定具有不变的数学形式，一个在任何参照系下不变的数学形式。也就是，一定要将狭义相对性原理拓展到广义相对性原理。

1915年6月，爱因斯坦前往德国哥廷根大学做系列讲座，在这里他遇到了一个高人，就是前面让大家猜测的高人，他就是20世纪最伟大的数学家——希尔伯特。他俩见面后，爱因斯坦迫不急待地向希尔伯特介绍他的广义相对论，同时说出了他遇到的数学困难。希尔伯特听后，三言两语，便让爱因斯坦茅塞顿开。返回柏林后，他又开始鼓捣自己的那个方程，想让它脱离对参照系的依赖。

虽然爱因斯坦离开了哥廷根大学，但希尔伯特却深深地被半成品的广义相对论迷住了。他也开始进行鼓捣了。大家猜一猜，谁鼓捣得更快？有人说，爱因斯坦搞了那么多年，希尔伯特咋能一下子就上手？那没办法，人家聪明嘛，结果也就是不到半年，希尔伯特就搞出了爱因斯坦八年都没有搞出来的方程。

爱因斯坦后来也搞出来了，比希尔伯特晚了五天。这好像也有点太巧了，所以谁拥有这个方程的优先权就发生了争议。研究科学史的发现，在这半年中爱因斯坦与希尔伯特一直在通信，而且希尔伯特一直在告诉爱因斯坦：他已经搞出来了。这弄得爱因斯坦很焦虑，他废寝忘食，奋起直追。甚至，似乎有资料表明希尔伯特在公开自己的方程时，事先寄给了爱因斯坦。这事当时就有争论并延续至今。但事情是这样平息的，希尔伯特主动出来澄清：“是爱因斯坦完成了广义相对论，而不是一个数学家。”是的，希尔伯特贡献的只是数学技巧，而爱因斯坦呈现的是对宇宙的洞察力，所以我们现在把这个伟大的方程称之为爱因斯坦方程。

让我们以无比崇敬的心情来瞧一瞧这个方程，看看它究竟长什么样，和爱因斯坦最初构建的方程有多大区别。原来的方程是：

R_μν＝KT_μν

其中，R_μν就是里奇张量，T_μν就是能量动量张量。现在更新的方程是：

两相比较，就是在左侧增加了一项，让R_μν再减去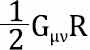。g_μν是度规张量，那g_μν乘以的R是什么，有人应该猜出来了，它和曲率有关系。还记得吗？里奇张量R_μν是从四阶的曲率张量缩并而来的，如果里奇张量R_μν再缩并一下，就成R了。为啥这个R不带角标呢？因为它就是一个分量。一个分量不就是标量吗？是的，R正是曲率标量。

左侧方程增加了这么一项，应该不是特别突兀，因为里奇张量就由度规张量g_μν及其一级和二级导数所构成，现在减去g_μν乘R的一半，也都是自家人，增增渐渐，肉反正是烂在了锅里。

有人肯定要问，减去这一项怎么了？原来的形式不更简洁、更优美吗？干吗非要减去它，搞得希尔伯特都出手了？谁要是这样问，就是忘了爱因斯坦刚才的困局了，原本的方程是简洁，但仍要依赖于参照系的选择，没有达到爱因斯坦广义相对性原理的要求。现在，一旦减去这一项，这个方程就永恒了，脱离了对参照系的依赖。也就是说，它在任何参照系下都有同样的数学形式。

让我们再来欣赏一下爱因斯坦方程：

我们如何来赞叹这个方程呢？我觉得所有词汇都显得那么苍白，因为这个方程里还蕴含了牛顿引力常数。方程中那个系数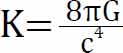，其中G就是牛顿引力常数，就是万有引力公式中的G。爱因斯坦方程中蕴含了牛顿引力常数，也就是爱因斯坦方程包含了牛顿方程。事实上，弱场情况下，爱因斯坦方程就会蜕化成万有引力公式，真的好神奇啊。

爱因斯坦方程经常习惯上被称之为引力场方程，但实际上方程并没有直接表达引力场的物理量，只有显示曲率的度规张量和里奇张量，还有能量动量张量，所以叫曲率方程可能更加准确，因为它是表达时空曲率与物质分布状态的方程。之所以还叫引力场方程，是因为引力这个概念太有魔性，尽管爱因斯坦已经用弯曲时空取代了它，但它留给我们的影响还是令我们挥之不去，更何况弯曲空间就是其中的物质所导致的。所以说，度规、里奇张量这些抽象的数学概念，都与我们心中的引力息息相关，所以一般还叫引力场方程，或者爱因斯坦引力场方程，或者爱因斯坦方程。

让我怎么赞美你，爱因斯坦引力场方程！笔者实在词穷，还是听听希尔伯特的博士生、量子力学的奠基人玻恩是怎么评价的：“人类思考自然的最伟大壮举，哲学思辨、物理直觉和数学技巧最令人惊艳的结合。”让我们静默三秒钟，来表达对此方程的仰慕之情。一、二、三。

有人肯定会说，您太夸张了吧，不就是个方程吗？不，它是十个方程，R_μν是带下角标μ、ν的，所以是很多方程，一个二阶非线性的偏微分方程组。宇宙万物的规律都蕴含在这个方程组之中了。但大家必须注意：方程中只是蕴含着万物的规律，并未呈现出来，需要将方程解出来，才能看到其中到底有什么灵童仙子、妖魔鬼怪。

但求出通解是不可能的，只能去求特殊情况的解。微分方程无法求出的问题，笔者在《第二章科言幻语聊〈三体〉》中详细讲过，这里不再重复。

或许有读者还记得，我在《黑洞与平行宇宙》中说：宇宙的规律似乎都蕴含在了爱因斯坦方程之中，后来的人每从其中求得一个特解，都是解开了一个令人震撼的宇宙密码。这个震撼度往往令爱因斯坦本人都无法接受。

其中最有名的是：史瓦西从引力场方程中求出了黑洞，尽管爱因斯坦反对黑洞的存在，但史瓦西以史瓦西黑洞名垂青史。在史瓦西的激励下，其他科学家继续求解引力场方程，陆陆续续得出五种黑洞，直接把爱因斯坦搞疯了。这能怪谁？一旦引入弯曲时空的概念，黑洞必然会出现。包括白洞、虫洞、奇点等等，都是由曲率所形成的一种特殊类型而已。(www.daowen.com)

但本节不谈这些，谈谁？引力波，这是本章的主题。新闻上老说爱因斯坦预言了引力波，他是怎么预言的，就是通过求解自己的引力场方程。刚才说那是个包含十个方程的偏微分方程组，而且是非线性的，不可能求出通解，只能在特殊情况下求解。但爱因斯坦知道自己数学不行，于是他玩了一个小把戏，将之线性化。这可以用中学的一个例子打比方。

我们在中学都学过单摆，它的运动方程就是非线性的，因为里面有sin θ这个项；但如果这个单摆摆动的幅度特别小，也就是θ特别小，那么sin θ就近似于θ了。一旦在运动方程中将sin θ换成θ，方程就线性化了，也就成了简谐运动了。但一定要注意，这个单摆的幅度一定要特别小。

好了，切换到引力场方程。它本是非线性的，如果假设这个引力场很弱，或者说时空弯曲的程度很低，那么就可以把方程线性化，这就叫弱场近似。一旦进行了这样的处理，爱因斯坦方程直接就变成波动方程了，解出来的当然就是波，也就是解的数学式子是由正弦sin和余弦cos所构成。这个波就是曲率波，一般把它叫引力波，这就是所谓的爱因斯坦预言了引力波，而且他还算出引力波是以光速来传播的。

这么大的事就这样说了，是不是太粗糙太轻浮了？那就再描述一下这个引力波的样子。它是个四极引力波。首先从解的形式看，引力波是个横波，它的震动方向与传播方向是垂直的。而且它有两种偏振，每个偏振中又有两个偏振方向，所以一共是四个偏振方向，它们之间的夹角是45°。大家脑海中是否能呈现出这样一图景：在XY平面上，一个空间曲率在四个方向上来回收缩，同时又将这个收缩沿着Z轴向前传播。这就叫四极辐射的引力波。

我们再举个例子，来形象地看看四极辐射的引力波。神话中常说，某大神是三头六臂，而这个四极辐射的引力波就是无头八臂，怎么讲？想象一个没有头的大神，但是他有八条胳膊，也就是四双胳膊，然后想象这四双胳膊都伸展开，每双胳膊都形成一条直线，是不是就呈现出四条交叉的直线？而且它们之间的夹角还是45°，就是八条胳膊均分了平面上的360°。好了，现在伸直四双胳膊的大神开始向前走了，而且还是以光速向前走；走的同时，四双胳膊还来回收缩，这就是四极辐射的大神，也就是四极辐射引力波。

6-18 四极辐射引力波

是否能探测到这个引力波，取决于其辐射功率的大小。在其辐射功率的数学公式中，有一个分母是C的五次方。想一想，三十万的五次方是个多大的数字？而且放在分母上，导致这个辐射功率低得仿佛蚊子嗡嗡叫，怎么可能观测到？所以爱因斯坦虽然预言了引力波，却无法验证。

我们如何找到功率相对强的引力波呢？也就是要找到引力场变化特别大的情形，这就必须要请黑洞粉墨登场。

黑洞是什么？它质量极大，体积还特别小，它对周围时空会产生强大的弯曲，简直就快要把时空弯断了。换句话说，它形成的引力场特别强大。但我们还是要用弯曲时空的语言来讲，虽然有些抽象，很难想象四维时空的极度弯曲。

继续把滚床单的例子拿过来。四个人扯平一个柔韧度极强的床单，这时在床单中央放一个铅球，床单是不是就被压弯了？现在想象一下，把铅球的质量增加一百万倍，同时铅球再缩小十倍，这个床单会怎样？这个超高密度的铅球还不把床单压破了？别这样想，刚才假设这个床单的柔韧度是极高的，所以压不破，只是这个铅球会在床单上陷下去，形成一个深深的洞，而且这个洞邻近的床单也极度弯曲了。如果你在它周围的床单上滚玻璃球，这个玻璃球必然会螺旋式地落入到这个深深的洞里，再也出不来。这个深深的洞，不就是黑洞吗？床单上的黑洞。它是怎么形成的？就是因为铅球质量特别大、体积还特别小。

这个滚床单的生动类比，是笔者借鉴的，但这里要拓展一下。就是在这个床单上再放一个质量特大、体积特小的一个铅球，这样床单上就会形成两个深深的洞，对吧？它俩周围的床单都不知道被弯曲成啥样了。但只要这两个铅球不动，床单再弯曲也是静态的。

此时我们要折腾一下，我们也东施效颦，学爱因斯坦的大脑实验，在想象中让这两个铅球互相绕着对方转动，而且速度还特别快。这个景象有点壮观，你能想象出来吧？分别陷入两个深深的床单之洞的铅球，还互相绕着高速旋转，这床单能受得了？能，因为我们用的是极度柔韧的床单。但随着两个铅球高速绕动，这床单就不得不疯狂抖动。而且洞越深，转动越快，床单抖动得就越凶猛。但不是胡乱抖，是形成了一定规律的波浪式抖动，这不就是引力波吗？而这两个深深陷入的铅球就是黑洞双星系统。

所谓黑洞双星系统，就是两个黑洞互相绕着对方转。有了滚床单的经验，我们可以想象，每个黑洞在嵌入的宇宙表面形成了深坑，也就是极大的时空曲率。当黑洞互相绕着对方旋转时，两个转动坑产生出极大变化的曲率波，以光速向外传播。这两个黑洞的场子，是我们现在能想到的最强的引力场，或者说是最大曲率，那么这种曲率的变化所引发的曲率波，或者说是引力波，就可以特别特别大，这样地球上的人类就有观测到的可能性了。此番LIGO就是观测到了双黑洞合并所传来的引力波。

但两个黑洞为何会合并？大家想想，双黑互转释放引力波，那是要消耗自身能量的，也就是变化的时空曲率把能量带走了。双黑能量一降低，就保持不了那个距离，就要靠近一点。或者这样理解更容易，向外传播的引力波会对黑洞产生反冲力，就像开炮时会有后坐力一样。黑洞一被反冲，两个黑洞就会靠得更近、转得更快，这样双方就会螺旋式地慢慢落向对方。而且越是靠近，就会转得越快，放出的曲率波就越强，失去的能量就越多，最终两个黑洞以接近光速融为一体，这就是黑洞合并。

太壮观了，可惜我们都没见过，黑洞里连光都出不来，怎么可能去观测！但是，有一个东西出来就提供了这种可能，谁啊？曲率波，也就是引力波，而且这个引力波的强度还特别大，尤其是在双黑合并的瞬间超级大，这就为人类检测到引力波提供了可能性。

地球人到底怎么观测宇宙中传来的引力波呢？这里再展开说一下。刚才一直说引力波实际上是曲率波，是时空弯曲程度不断变化的传播，所以当它传过来后，我们的时空就会一张一弛、一松一紧。具体来说，引力波会在一个方向上拉伸，在另一个方向上挤压，拉伸和挤压是振荡的。当引力波的波峰到达时，是上下拉伸、前后挤压，当波谷来临时，就变成了上下挤压、前后拉伸，如此反复不已。这样的话，我们不就可以观测了吗？

但大家要注意，虽然黑洞合并释放了巨大强度的引力波，但是黑洞离我们太遥远了，所以当引力波传到我们这里时，其早都衰得不成样了，早已没有往日的雄风，是所谓“强弩之末，势不能穿鲁缟者也”。具体来说，两个黑洞合并所产生的引力波对地球物体所产生的变形只有物体大小的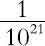。小到这种程度，真有点让人绝望，而且已经是双黑洞合并的级别了，还怎么让科学家观测？

沧海横流，方显英雄本色；曲波渺小，偏有韦伯要测。1959年，约瑟夫·韦伯手提一根长两米的铝棒，要用它测量遥远宇宙传来的引力波。韦伯提着两米的铝棒子，要去测量曲率波，这太有画面感了，我脑海中浮现的不是堂吉诃德，而是当阳桥前喝退百万曹兵的张翼德。

韦伯是这样想的，一旦引力波袭来，就会挤压和拉伸铝棒的两端。当然这里还用到了共振原理，很复杂，我们就不深究了。10年后，即1969年6月，韦伯向全世界庄严宣布：“我发现了引力波。”但是，因为其观测不具有可重复性，所以没得到承认。但韦伯作为观测引力波的先驱，获得了世人的尊敬。

大家没有承认韦伯的观测，还有一个重要原因是觉得他那个铝棒子没有灵敏到能够感受如此微弱的引力波。所以很多人开始尝试制作更好、更长的铝棒子，或者是银棒子、金箍棒之类，反正就是各种棒子。

20世纪60年代，有两个苏联人用俄语说：不要用棒子啦，那是不行的，要用干涉仪。再后来，美国人设计出了干涉仪探测器，从此棒子时代结束，激光干涉仪探测引力波的时代到来了。

此番LIGO测到引力波正是用的这种激光干涉仪，这已经说过了。

现在我要解答这样一个困惑。其实这也是我最早的困惑，就是LIGO检测到了一个信号是不假，但凭什么说这就是一个引力波带来的扰动，而不是其他噪声引起的？比如某国爆炸了一个小型核武器。尤其令我感到困惑的是，LIGO还绘声绘色地说，这引力波是两个黑洞合并所产生的。在那一刻，我觉得LIGO简直就是由一帮骗子组成的，尤其是那个发言人，面露自得之色，一时分不清是翩翩风采还是骗子风采。

笔者的质疑精神特别强大，对任何观点或结论，不在乎你是多大的专家或权威，就是要看你的论证。当时为何觉得LIGO是骗子，理由是这样的！LIGO宣称它发现了引力波，而且是两个黑洞合并所形成的引力波。当时觉得很扯淡，首先人类就没有直接观测到任何黑洞，因为它连光都出不来，你凭什么去观测？但有人说，我们可以观测黑洞发出的引力波，问题是引力波之前也没有观测到啊。用两个都没有观测到的东西，都是从爱因斯坦方程中解出来的东西，竟然要互相证明对方的客观存在性，这在逻辑上成立吗？

但转念一想，LIGO绝非普通机构，而且它一宣布，好像业内认可的人还不少，既然如此，必然有其道理，值得去看看。于是我翻阅了他们发表的论文，事情原来是这样的：

LIGO及其他机构的科学家早就在理论上构建了双黑洞合并的数学模型，然后对它俩高速环绕、最终合并的过程进行了计算机模拟，并计算出所发出引力波的波形。这个波形有其自身的特点。换句话说，如果一旦LIGO从宇宙获得一个信号，而且这个信号与计算机算出的波形几乎一致，它反过来就会说：这个信号就是引力波，而且是两个黑洞合并所产生的引力波。

不晓得大家是否理解这个逻辑，就再打个比方吧。我们在现实中没有见过饕餮这种怪兽，也没有见过谁能一次把两吨苹果吃完。但通过神话发现，饕餮可以一次性吃完两顿苹果，而且连苹果核都会吃进去，但会留下苹果把儿。于是我们把两顿苹果放在旷野里，来观测饕餮的出现。结果有一天，我们发现两吨苹果都没了，就只剩下了一堆苹果把儿，于是我们庄严宣布：我们观测到了饕餮，证明了饕餮的存在。就是这个逻辑。

这个推理是合理的，但有漏洞。万一麒麟也可以这样吃两吨苹果，发现饕餮的结论是不是就出问题了？所以LIGO发现引力波是否正确，取决于计算机模拟出来的信号是否具有极大的特殊性，特殊到非黑洞合并不可能有这种波形的程度，才能断定所接受同样波形的信号一定是引力波信号。

当然，LIGO的科学家是有这个信心的，再说科学上的事就是带点儿朦胧感，哪里有百分百的事儿，科学不在于其正确性，而在于它可以证伪。更何况，这样一个发现的确很重大，LIGO必须要尽快公布、抢先发表，这关系到很多世俗的事。科学是不食人间烟火的，但科学家还是要获得鼓励的。

笔者在此向LIGO表示祝贺，祝贺他们在人类探测引力波的历史上，做出了里程碑式的贡献。但我还有一个小小的期待，希望LIGO能如此这般地加以验证，那引力波的存在就更加铁定无疑了。是的，我像诗人海子一般，也有一个期待。