明白了四维时空，现在要了解四维时空的曲率，因为引力波就是四维时空曲率的传播。但曲率是一个纯粹的几何概念，是用来描绘空间弯曲程度的一个数学概念，要了解它，我们要先从简单的平直时空说起。或者干脆就从最简单的经典空间说起吧。

在经典物理中，空间与时间是完全分离的，所以只需要考虑三维空间，而且它也是平直的，根本没有什么弯曲的概念。这特别符合我们的常识，也是牛顿的想法。

平直的三维空间称为欧几里得空间。欧几里得空间，大家千万不要觉得陌生，我们在中学学的平面几何和立体几何都是欧几里得几何，就连解析几何也不过是用代数的方法来解决欧几里得空间中的问题。大家没忘那个平面直角坐标系吧，互相垂直的XY轴，这是笛卡尔研究出来的，所以又叫笛卡尔坐标系；如果要解决立体几何的问题，那平面直角坐标系就不够了，要再画一个Z轴，垂直于XY轴所形成的平面，这样就形成立体直角坐标系，这当然也是笛卡尔坐标系。

在欧几里得空间中，如果建立起笛卡尔坐标系，那么空间中的任何一个点，都可以用xyz的三个数值来表示。这里可以先用二维平面来说，再推广到三维空间。

我们现在画一个直角坐标系，就是画一个互相垂直的XY轴，XY轴的交叉点就是原点O，这时我们随便在平面中标出一个点A，就可以用坐标x和y来唯一标定它的位置，即A（x，y），其中x就是这个点距离Y轴的垂直距离，而y就是这个点距离X轴的垂直距离。比如说A（3，4）就是指A点的横坐标是3，即它距离Y轴距离是3，纵坐标是4，即它距离X轴的距离是4。这时我要问了，A点距离坐标系原点O的距离是多少？用勾股定理，也就是3的平方加上4的平方等于5的平方，所以点A（3，4）距离原点O的距离就是5。

现在考虑这个平面上有甲乙两个点，坐标分别是（x₁，y₁）和（x₂，y₂），那么甲乙两个点的距离s是多少？无非是将两个点坐标的差值进行勾股定理，于是得出甲乙距离s²＝（x₂-x₁）²＋（y₂-y₁）²。

我们在中学时喜欢把差值记为希腊字母Δ（delta），所以这里的距离也可以表达为：s²＝Δx²＋Δy²。

现在继续假设甲乙两点挨得特别近，两点间的距离非常小。有人会说，甲乙两点无论距离远近，反正都是s²＝Δx²＋Δy²，你刻意说这种情况有什么意义？意义大了，但此时不方便说。但请大家注意，在数学上差值特别特别小的情况就不再用Δ来表达，而是用d表示，比如dx就是表达甲乙两个横坐标之间非常非常小的差值。学过高等数学的人知道，这是在说微积分的微分。微分就是很小很小的差值，用小写的d来表达。

6-6 微分形式的勾股定理

这样一来，挨得很近的甲乙两点的距离公式，用微分表达式就成了ds²＝dx²＋dy²。有人会说，怎么s也d了一下？因为距离很近很近。好，大家一定要记住：挨得很近的甲乙两点的距离公式是ds²＝dx²＋dy²。说白了就是勾股定理，这一定要记住，不然就会越来越费劲。

刚才说的是平面的情况，现在要将之推广到三维欧几里得空间，这样挨得很近的甲乙两点的距离公式是什么呢？当然我们首先要建立立体直角坐标系，有了XYZ轴，才可以对空间中的任意一点给出坐标（x，y，z）。我们把刚才在平面中的公式直接推广到三维空间——挨得很近的甲乙两点在三维空间中的距离公式是：ds²＝dx²＋dy²＋dz²。感觉还是挺顺的，不放心的朋友可以自己推导一下，不过是用了两次勾股定理；或者你洋气一点儿，先用了一次勾股定理，再用了一次毕达哥拉斯定理，中西结合，微分距离终于搞定啦。

6-7 三维空间中的微分勾股定理

说这些到底想干啥？在经典物理学中，也就是在常识中，一个刚体上两点的距离是否会因为刚体的运动而发生变化？刚体，就是在运动中形状和大小都不变，而且内部的各个点的相对位置也不变的物体。比如一个标枪就是刚体，但人就不是刚体，人在跑步的时候，两腿间的距离会不断变化。回到原来的问题，在我们的常识中，一个刚体上两点的距离是否会因为刚体的运动而发生变化？就是说标枪上两个点的距离是否会因为标枪在空中飞行而发生变化？不会，绝对不会。这一点，牛顿是这样认为的，伽利略也是这样认为的，亚里士多德更是这样认为的。先别偷着笑，我们要把这个经典的观念用数学严格表达出来。是的，又要说数学公式了，就为真正了解引力波。

现在我们讨论相对速度是v的两个惯性系上的观察者，对某个运动物体的描述有无差异。这听起来很别扭，两个惯性系等等，其实与火车相对地面以速度v匀速行驶，来看地面观测者和火车上的观测者对同一个物体运动的描述，在本质上并没有什么不同。

也就是说，我们要以两个观测者的各自角度来看待同一件事，所以需要各自建立笛卡尔坐标系，也就是立体直角坐标系XYZ，分别表达前后、左右、上下。一个坐标系与地面绑定，就是以地面观测者为中心所建立的坐标系；另一个坐标系与火车绑定，也就是以火车观测者为中心所建立的坐标系，下面我们用客车表示。

为了生动直观，我们假设这两个观测者是父子俩，父亲到火车站送儿子去远方。此时客车待发，父子俩依依惜别，儿子从车窗伸出胳膊，紧紧地抱住了父亲的肩膀，说了一句话，父亲听后，禁不住泪流满面。父亲从来都没有流过泪，这一回终于没有忍住。儿子到底说了啥？有人开始猜测了，儿子说的是：“我要去寻找引力波！”别瞎猜了，还是听我说，是做了一首诗：“男儿立志出乡关，学不成名誓不还；埋骨何须桑梓地，人生无处不青山。”希望大家以这种精神，坚持吃完引力波这道硬菜——埋骨何须桑梓地，人生处处曲率波。

6-8 父亲送儿子，两眼泪汪汪

讲这个故事不只是为了励志，更想告诉各位，地面观测者父亲和火车观测者儿子在火车未启动前，处于同一空间位置，随后客车就沿着地面坐标系的X轴向前行驶了。也就是说，儿子所在的客车坐标系开始以速度v沿着X轴方向向前运动了，那会如何？双方看待事件的感觉就不一样了。

我们假设父子的眼睛都很好、看得很远。这时有一辆货车在X轴上反方向行驶过来，那么地面上父亲感受到的货车距离与客车上儿子的感受就不一样。这真是废话，儿子的客车是迎着货车上去的，当然觉得近，而父亲在原地没动，就会觉得货车还比较远。我们把货车在地面坐标系中的坐标表达为（x，y，z，t）。怎么还有时间t？因为货车一直在动，每一个时刻的坐标点（x，y，z）都可能不一样，所以描述货车还需要时间点，而货车在客车坐标系中就表达为（x'，y'，z'，t'）。别忘了，客车在以速度v沿着X轴向前运动。

6-9 地面为参考系时，货车的速度和坐标

6-10 地面为参考系时，货车的速度和坐标

这两组坐标（x，y，z，t）和（x'，y'，z'，t'）就是地面上的父亲和火车上的儿子分别对货车时空位置的描述。那么两者的关系应该是：

x'＝x-vt

y'＝y

z'＝z

t'＝t

解释一下，因为客车是迎着货车开过去的，所以客车上的儿子所感受的货车距离要比地面上的父亲更近一些。近了多少呢？就是客车速度乘以行驶的时间。这也就是儿子远离父亲的距离，所以有x'＝x-vt。为何在另外两个方向上就是y'＝y，z'＝z呢？因为客车是沿着X轴向前运动的，它在垂直的Y轴和Z轴方向就没有任何运动，也就是儿子与父亲在上下和左右这两个方向并没有发生相对移动，所以就有y'＝y，z'＝z。

为何t'＝t呢？因为父亲和儿子是同时开始计时的。有没有问题呢？估计有读者不愿意了，起始时间一样又如何，前面不是说过，运动物体的时间会膨胀吗？t'是要膨胀的，怎么会等于t呢？你要这样说，我就太高兴了，说明前面没白讲。但是在这里，我还是要说t'＝t，因为我们是在讲经典物理。

好，现在把刚才说的四个数学等式放在一起，就是：

x'＝x-vt

y'＝y

z'＝z

t'＝t

在经典物理中，我们把这组公式称之为伽利略变换，其表达的是两个相对运动的惯性系之间的变换。这个变换太符合我们的常识了，所以也特别好理解。因为t'总是等于t，所以都没有必要考虑这个等式，根本就不需要写出来，它就在人们的心中，心照不宣，不证自明，仿佛荣格所谓的“集体无意识”。

当然，我们现在知道它是有问题的，因为我们已经站在了爱因斯坦的肩膀上，看到了伽利略和牛顿的脑门上，长了一个很经典的瘊子。

在伽利略变换之下，可以发现一个不变量，就是无论地面上的父亲还是客车上的儿子，他俩对货车上某两点之间距离的观测是完全一样的，这是因为距离是坐标之间的差值。虽然处在不同坐标系对于X方向有vt的差别，但做减法时就消掉了。也就是刚才说的，刚体之间邻近两点的距离ds²＝dx²＋dy²＋dz²在不同的参照系下是不变的，即标枪不会因为其飞行而改变其上两点间的距离。

总之，大家记住，在经典物理学中，不同惯性参照系的变换叫伽利略变换，变换过程有一个不变量，就是两个空间点之间的距离，也就是说长度是一个绝对量，不会因为参照系的不同而发生改变。

但现在我们已经知道，这种认识是不对的。物理学家为何抛弃了伽利略变换，就是因为迈克尔逊-莫雷实验。我在第五章讲了，这个实验的结果太“雷人”，令当时的物理学家绞尽脑汁想解决这个问题，甚至提出了以太拖曳理论，但都不太靠谱。

这时洛伦兹站出来了，他说：任何物体在相对于以太的运动方向上，其长度都要收缩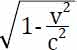倍。这下子，迈克尔逊-莫雷实验中没有测到干涉条纹移动的结果获得了解释。但洛伦兹并没有觉得自己很“二”，可以说他有“二”的行为，但没有“二”的心。他觉得自己纯粹是拼凑，为赋新词强说愁，纯粹是为了解释实验结果而进行的数学拼凑，并没有感觉到这个拼凑中的物理价值。

但是，当小年轻爱因斯坦看到这个拼凑后，如获至宝，直接将洛伦兹变换作为狭义相对论的基础。具体来说，爱因斯坦抛弃了洛伦兹仍坚守的以太基础，直接将洛伦兹变换作为两个惯性系之间的普遍变换，替换了经典物理学中的伽利略变换。

洛伦兹变换，大家应该如雷贯耳，第四章就提到它了，只是当时没说它的数学形式，但今天是豁出去了，不说不行。它的数学形式就是：(www.daowen.com)

真的有点儿复杂。我们把它和伽利略变换比较一下，伽利略变换中x'＝x-vt；但洛伦兹变换中相减后还要除以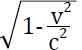。其中的c是光速，v还是客车的坐标系相对于地面坐标系的速度。大家都知道，火车的速度最多也就时速500千米，这和光速每秒30万千米相比简直可以忽略不计，所以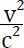就几乎是0，所以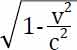就几乎是1，这样的话，洛伦兹变换就退化成了伽利略变换，这就是为什么生活中感受不到相对论的效应，因为我们生活在低速的环境中。想象一下，如果火车的速度v达到光速的一半，那么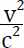就是一个响当当的数字了，这样洛伦兹变换的效果与伽利略变换就完全不一样了。

刚才只分析了第一个等式，第二和第三个等式与伽利略变换完全一样，没必要多说。再看第四个等式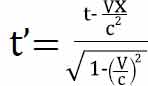，好复杂，好凌乱。但你从中看到了一种气质，就像我们不知道怀素写的什么字，但看到了一种气质：狂、草，又狂又草；那么从这个公式中看到了什么？看到了t变成t'之时，里面蕴含了相对速度v、光速c，尤其是看到了空间坐标x。这意味着什么，意味着时间和空间发生作用了。用爱因斯坦的话说，就是时间和空间搅和在一起了，无法分离了，所以我们必须要用四维时空来看待这个世界。

在洛伦兹变换下，刚体之间邻近两点的距离在不同的参照系下不再是不变的了，两点距离会发生收缩，就是所谓尺缩效应。比如说一根棒子静止的时候长度为L₀，一旦以速度v运动，静止的观测者就会觉得棒子的长度缩短了，具体为。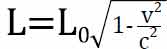

但在日常生活中，我们看不到尺缩效应。谁让光速太大了呢？否则高速旋转的人还不个个都腰细如柳了吗？这里要提醒大家的是，静止的人感觉运动中的棒子缩短了，但骑在棒子上的人会觉得棒子的长度一点没变，也就是说一切都是相对的。

其实这也挺好理解，有时你觉得人家穿大红大绿挺俗气，但人家自己觉得挺好，如果你真的能进入人家的心理状态，你也会觉得大红大绿挺好。你看别人大口吃泡菜时，自己嘴里的牙齿都觉得很酸，但人家本人并没有觉得酸。就是这个道理，万物一理，岂有他焉？

总之，洛伦兹变换导致了尺缩效应，这意味着，在真实物理世界中，刚体之间邻近两点的距离在不同的参照系下观测，会出现不同的数值。

研究自然规律，就是要在纷繁变化中寻找其中的不变量。破坏了一个不变量，一定会有一个真正的不变量在等着我们。但我先不讲，让大家喘口气。

你一边喘气，我一边给你引进一个人物，他就是爱因斯坦的大学数学老师——闵科夫斯基。

话说爱因斯坦在十七岁上了苏黎世工业大学，成天翘数学课，躲在宿舍学物理，这令闵科夫斯基很生气，直接就骂爱因斯坦：“你这个懒狗，我的数学课都不好好听，将来会有啥出息！”

谁成想，爱因斯坦毕业后没多久（1905年）就创立了狭义相对论，这令闵科夫斯基很吃惊，原来是阿尔法狗加贝塔狗？转念一想，“这娃当年没好好听我的数学，他咋就能搞出狭义相对论？”狐疑中把学生的论文拿过来一看，发现论文里面确实只用了一些很简单的数学。

在闵科夫斯基看来，爱氏的理论虽然在物理上极具突破性，但在数学形式上不怎么优美——看，当年没好好听老师的课吧。于是闵科夫斯基觉得有必要帮一下这个老翘课的学生，于是开始研究相对论，最后果然把狭义相对论的颜值大大提高了。

具体是这样的：洛伦兹变换虽然破坏了两点距离ds²＝dx²＋dy²＋dz²的不变性，但是发现了一个新的不变量，大家猜猜这个新的不变量里面增加了谁？有人可能就喷了——我们读懂已经是勉为其难了，还让我们猜没讲的，把我们当啥了？其实还真不太难，想一想洛伦兹变换与伽利略变换的不同就可以猜出来。就是两点不同，洛伦兹变化中出现了光速c，再者洛伦兹变化中时间t与空间x混合在一起了，所以这个新的不变量中必然会有光速c和时间t。原因在于，大家都在变，那么把所有变量都凑在一起，就有可能造出一个不变量。

具体来说，这个不变量就是：

dx²＋dy²＋dz²-c²dt²

这个量不就是原来经典物理的不变量减去c²dt²吗？也就是两点空间距离再减去c²dt²。

有点儿意思，虽然在不同惯性系下邻近两点的空间距离变了，但是如果让它减去c²dt²，那么就是一个新的不变量。这正体现时空一体的新理念。

这是洛伦兹变换中自然引出的推论，但闵科夫斯基作为一个数学家，感觉这个新的不变量看着不顺眼，不具有数学上的对称性。四个微分相互加减，前面是三个平方相加，看着挺美，后面突然是减法，感觉不爽，而且减去的dt²还乘了一个系数c²，也不太美气，咋办？那就变一变呗，这对搞数学的人是容易的一件事，他直接搞了一套新的符号，把这个东西整容了。

具体是这样的，他把x₁替代x，x₂替代y，x₃替代z，这些还真没啥，关键是最后一项——减去c²dt²怎么处理？他让x₄替代ict。各位朋友，i是什么？大家还记得吗？-1开平方是多少？-1开平方是虚数，是虚数单位i，那么i²＝-1。这样，一旦让x₄＝ict，意味着dx₄²＝-c²dt²。经过这样一番改头换面，洛伦兹变换下的新不变量dx²＋dy²＋dz²-c²dt²。就变成了：dx₁²＋dx₂²＋dx₃²＋dx₄²大家有没有觉得很美、很整齐？仿佛这个不变量就是三维欧几里得空间不变量的一个直接推广而已。

肯定会有人发问，做这个整容有啥意思？意思很大，这里先说点小意思——从数学上来说，我们原来把xyz作为一个空间点，或者说把（x₁，x₂，x₃）作为一个空间点，现在可以很自然地将（x₁，x₂，x₃，x₄）作为一个空间点。当然前三个是空间坐标，最后一个x₄是ict，是时间坐标，但闵科夫斯基写成这种形式，让我们从心理上觉得，空间与时间至少在形式上是对等的，从而突破了空间和时间风马牛不相及的传统观念。

我们现在把这种四维时空称为闵科夫斯基空间，简称闵空，它与我们熟悉的三维欧几里得空间（简称欧空）是很不一样的。欧空就是我们中学学的那种几何空间，或者说常识中的三维空间。闵空与欧空的差异不在于几维，我们完全可以把三维欧空拓展到四维，就是画一条垂直于正方体的直线，不就可以形成第四维了吗？什么？这没法想象？我也想象不来，就是想表达，欧空也可以超过三维，但都是空间维度，而闵空是多了一个时间维度。

所以，闵空与欧空的差异在于欧空是纯空间，而闵空引入了时间维度。

换一种方式说，闵空把时间视作了第四个维度，而且将时间与三维空间融为一体，从而将物理世界视作四维时空。在四维时空中发生的每个事件，都可以用时空坐标来定位，也就是xyzt，或者说是x₁x₂x₃x₄，这就是世界点。既然如此，两个事件之间就会有一个间隔，如同三维空间中的两点有一个直线距离一般。三维空间的距离ds²＝dx₁²＋dx₂²＋dx₃²，那么四维时空中两个事件的间隔不就可以定义为ds²＝dx₁²＋dx₂²＋dx₃²＋dx₄²吗？注意，这是定义，换句话说，是一种规定，但这个规定听起来很有道理，就是三维空间距离在四维时空中的延伸。正是闵科夫斯基的整容，才使得这个延伸显得特别自然。

而且这个规定，也就是两个事件的间隔，在洛伦兹变换下还是不变量。于是闵科夫斯基非常亢奋地宣称：这是四维时空中两个事件的一个绝对间隔，无论在哪个惯性系下计算，它的数值都是一样的，所以这个绝对间隔就相当于三维空间中两个点的直线距离。

闵科夫斯基好强啊，不愧为爱因斯坦的老师。但学生对老师的这个数学处理是什么态度呢？起初是很不以为然的，爱因斯坦觉得闵科夫斯基用数学掩盖了定律背后的物理意义，用x₄代替ict，搞得大家都忘了x₄里面蕴含了时间t。正因为这样，有些相对论书中还是不用闵科夫斯基的那套符号，还是用那个事件间隔的表达式，即：

ds²＝dx²＋dy²＋dz²-c²dt²

这样看着虽然颜值不高，但是心里很踏实、很安全。

爱因斯坦一开始不喜欢他老师这一套美妙的数学形式，但四年之后，他认识到，要想搞广义相对论，没有闵空这套东西根本就没法往下走。爱因斯坦此时眼含泪水，想对老师说一声：“闵老师，我错了。”但他已无处可说，因为老师已经去世了。

这真是：子欲养而亲不待，徒欲尊而师不在。

好了，我们化悲痛为力量，努力学习相对论，向闵老师、爱老师致敬。

现在我们要讲一个概念，这个概念是一块硬骨头，它就叫“度规”。这是通往引力波的一个拦路虎。

度规就是在一个坐标系中，用来描述一段很短的线段长度的方式，换句话说，度规就是定义在某个坐标系中度量两点之间长度的规矩。说得好抽象，其实就是在说啥是长度。你拿根棒子说很长，我反问你，凭什么说它长，长度的定义是什么？我还觉得我手中的桃子很长，因为把这桃子皮剥下来，切成细丝连起来，可以绕地球一周。当然，这是故意抬杠，目的是为了让你思考长度的定义。

我们日常生活中对长度的定义还是有共识的，只不过大多数人表达不出来，其实就是两端之间的直线距离。用数学语言表达就是，在三维欧几里得空间中，两个邻近点之间的距离就是连接两点的直线的长度。若建立笛卡尔坐标系，这两个邻近点之间的距离公式就是：ds²＝dx₁²＋dx₂²＋dx₃²。这就是欧几里得空间的度规，也就是对两点之间距离进行度量的规矩；换句话说，在欧几里得空间，就是这样度量长度、度量距离的。

我们不妨思考一下，这个距离ds的平方正好就等于dx₁²＋dx₂²＋dx₃²，为什么其中没有dx乘dy，或者dx乘dz的二次项存在呢？幸亏没有，若要有了就太麻烦了。好了，反正三维欧几里得空间的度规就是ds²＝dx₁²＋dx₂²＋dx₃²。

同样，在四维闵科夫斯基空间的度规，正是刚才讲过的事件间隔：ds²＝dx²＋dy²＋dz²-c²dt²；也就是说，闵空中两个事件之间的距离，当然我们叫事件间隔就是用这个公式来度量的，就是闵空的度规。

大家再想一想，这个公式里为何也没有dx与dy、dz或dt的乘积项呢？若要再出现个dx乘dt，那才叫热闹。

这样看来，三维欧空的度规与四维闵空的度规还颇为相似，都没有交叉项的存在，都是自己和自己的平方。

但两种度规有一个本质的差异，就是闵空引入了时间，这使得闵空度规中有一个时间项，而且这一项是带负号的。这使得闵空中的事件间隔ds²可以是正的，也可是是负的。在欧空中这有点不可想象，距离ds²怎么能是负的？可以说，狭义相对论中的各种光顾陆离、各种不可思议，都可以视作闵空或度规中的减去c²dt²在作怪。

无论如何，闵空度规还是比较简单的，没有交叉项。原因在于，它处理的是平直的时空；一旦时空弯曲，度规中就会出现交叉项，就将面临更大的挑战。

好了，刚刚经历度规洗礼的伙计们，我们要不要一起去迎接这个挑战，到广义相对论的百花园转一转，看看那弯曲的空间里一切是否平权？如果你愿意，我们走吧。