由于常温下[C4mim][PF6]在约0.5 GPa发生相变，当压强低于0.5 GPa，样品为液态，当压强高于0.5 GPa时，样品呈晶态。根据不同的相态区域，选择适当的物态方程模型，从而提高物态方程的可靠性。

当压强低于0.5 GPa时，[C4mim][PF6]为液态，仍然选用Tait方程对高压下[C4mim][PF6]的密度进行拟合。通过对两种实验方法所获得的密度值和Harris等(2005)提出的密度值进行拟合，拟合结果如表8-3所示。三种不同数据来源的拟合系数相差较大，其主要原因为:基于金刚石对顶砧的实验中，红宝石压标在较低压强时压强标定误差较大，而且[C4mim][PF6]的相变点压强较低，造成数据点较少；基于活塞圆筒装置的实验中，由于实验条件限制无法获得200 MPa以下的密度值，导致可获得密度的压强范围较小。图8-4为不同压强下密度的实验值和文献报道值经过拟合所获得的等温密度线。在300 MPa附近，基于金刚石对顶砧实验方法和活塞圆筒装置所获得密度值与利用文献中较低压强下的密度数据拟合后外推所获得的密度值之间的偏差分别约为3%和2%。这说明对于较低压强下或数据点较少的情况下，两种实验方法存在一定的局限性。

表8-3　压强低于0.5 GPa时[C4mim][PF6]密度的实验值和文献报道值利用式(8-1)的拟合系数

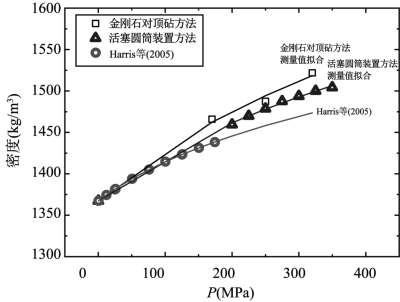
图8-4　常温(298 K)、压强低于0.5 GPa时[C4mim][PF6]密度的实验值和Harris等(2005)得到的值通过式(8-1)计算得到的曲线

图8-5为本研究中两种实验方法获得的密度实验值与计算值的相对偏差，两者相符度较好。基于金刚石对顶砧和活塞圆筒装置两种方法所获得实验结果的AARD分别为0.23%和0.07%，实验值与计算值近似。

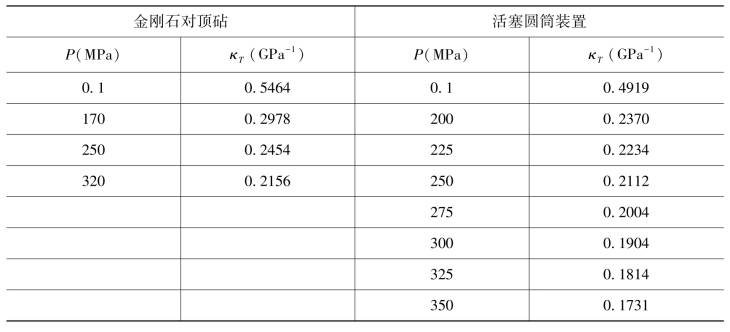
通过物态方程，我们进一步计算获得压强低于0.5 GPa时[C4mim][PF6]的等温压缩率κT，如表8-4和图8-6所示。如图8-6所示，随着压强的增加，等温压缩率κT逐渐变小，说明样品的可压缩性降低。

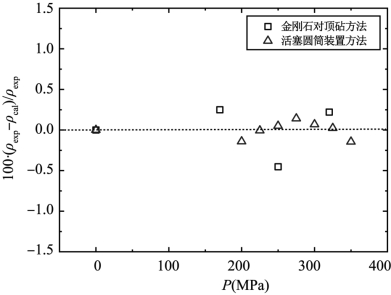
图8-5　常温(298 K)、压强低于0.5 GPa时[C4mim][PF6]密度的实验值与通过式(8-1)获得的计算值之间的偏差(www.daowen.com)

表8-4　压强低于0.5 GPa时[C4mim][PF6]的等温压缩率κT(常温298 K)

当压强高于0.5 GPa时，样品呈晶态。高压下固体的摩尔体积可以用二阶的Birch－Murnaghan方程进行拟合，该方程如下所示:

式中，V0和V分别为零压和高压下的摩尔体积；K0为零压下的体积弹性模量。不同压强下的摩尔体积可以通过不同压强下的密度进行计算。如图8-7所示，经过拟合，K0为12.4800 GPa，V0为184.8963 cm3/mol。

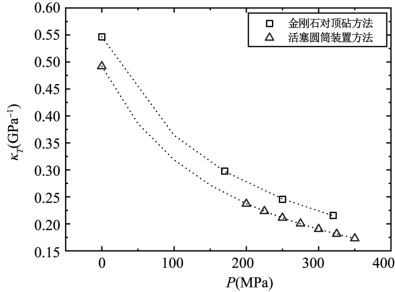
图8-6　常温(298 K)、压强低于0.5 GPa时[C4mim][PF6]的等温压缩率κT(虚线为数据拟合线)

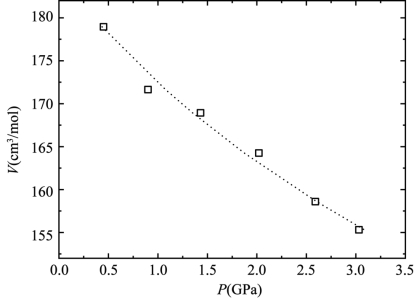
图8-7　常温(298 K)、压强高于0.5 GPa时[C4mim][PF6]的摩尔体积与压强的关系(虚线为数据拟合线)