当一个小球在液体中下落时，那么该小球将受到3个力作用:向下的重力G球＝m球g＝ρ球V球g、向上的浮力F浮＝G排＝ρ液gV排＝ρ液gV球和向上的黏滞阻力f阻(图6-5)。当小球所处的液体为理想情况(液体在各方向是无限广延的且无旋涡产生)时，小球所受到的黏滞阻力与速度关系将满足斯托克斯公式:

式中，f阻为小球下落时受到的黏滞阻力；η液为液体黏度；v球为小球下落速度；r球为小球半径。当小球由静止开始下落，由于小球的速度v球较小，所以黏滞阻力f阻也较小。在小球重力的作用下，小球速度v球将逐渐增大，f阻也随之增大。当小球速度增加至最大值并且不再发生变化时(小球做竖直向下的匀速直线运动)，小球所受到的3个力G球、F浮和f阻(图6-5)将达到平衡，则满足下列等式关系:

图6-5　小球受力情况

此时小球做匀速直线运动，运动速度为v0，也称为收尾速度。(www.daowen.com)

将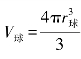代入式(6-4)得:

由于本研究的目的是为了原位测量高压条件下离子液体的黏度，需要将该黏度测量方法运用到金刚石对顶砧的样品腔内，所以小球将在圆柱形状的样品腔内做匀速下落运动。圆柱形状的样品腔毫无疑问不是无限广延的空间，不符合理想情况下斯托克斯定律的要求，因此必须考虑小球所处有限空间的边界效应，即黏度计算公式需要进行适当地修正，修正后的黏度计算公式为

式中，γ为修正因子。