随机微分方程的解的存在唯一性不同的意义在不同的场合使用,如果我们关心轨道或者Brown运动是预先给定的,那么我们需要考虑强解,反之如果我们只关心过程的分布或者构造一个过程,那么只需要考虑弱解就可以了.但是在大多数情况下,我们考虑方程的解就足够了,只有需要用同一个Brown运动构造不同的解的时候才需要用到强解.随机微分方程的存在唯一性理论有三大定理,下面第一个定理是说解的存在性和轨道唯一性一起蕴含有强解存在唯一性.

定理6.3.1　如果方程(6.1.3)有轨道唯一性,那么

(1)分布唯一性也成立;

(2)解的存在性蕴含着强解存在,实际上,存在一个适当的泛函F:Rd×Wr-→Wd,使得X=F(X0,B).

第二个定理是说系数b,σ的有界连续性可以保证随机微分方程解的存在性,矩阵σσT的一致正定性保证解的唯一性.

定理6.3.2　如果随机微分方程的系数函数b和σ在其所定义的空间上是有界且连续的,那么对任何给定的x∈Rd,存在解(X,B)使得X0=x.如果随机微分方程是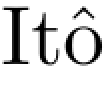型的,那么有界性条件可以去掉,并且当矩阵σσT是一致正定有界连续,b是有界Borel可测时,方程解的唯一性成立.

第三个定理是说对于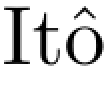型方程,系数b,σ的局部Lipschitz性质保证解的轨道唯一性.(www.daowen.com)

定理6.3.3　如果随机微分方程是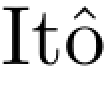型的且系数b,σ满足局部Lipschitz条件,那么方程解的轨道唯一性成立,因此由前一个定理,方程的强解存在唯一.

实际上,当方程的系数满足整体Lipschitz条件时,用Picard迭代的方法可以直接证明强解的存在唯一性,见下节.下面的定理是第三个定理的补充,是说在维数为1的时候,条件可以减弱:b满足整体Lipschitz条件,σ的条件只需要某种H¨older连续.

定理6.3.4　(Yamada-Watanabe)考虑一维Markov型方程,即d=r=1,满足对所有的t≥0,x,y∈R

(1)|b(t,x)-b(t,y)|≤C·|x-y|,

(2)|σ(t,x)-σ(t,y)|≤h(|x-y|),