常微分方程是描述确定性运动的方程,随机微分方程通常看成为是一个常微分方程加上一个由Brown运动驱动的随机扰动.例如

是一个描述利息的常微分方程,得到的是确定性的解.而最简单的随机微分方程Black-Scholes方程

表示增长率是一个常数加上一个随机扰动.随机微分方程也是由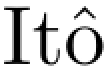首先引入的.

我们将简单地介绍下列形式的随机微分方程

其中B是一个r-维标准Brown运动,X是未知的连续d-维过程.随机微分方程是一个形式,因为实际上随机微分没有意义,随机的积分才有意义.因此上面的方程是指下列的随机积分方程

我们先对系数(b,σ)作个说明.

设Wd是[0,+∞)到Rd的连续映射全体,装备紧一致收敛的拓扑,用B(Wd)表示Wd上Borelσ-代数,Bt(Wd)表示由ww(s),s∈[0,t]生成的子σ-代数,Rd⊗Rr表示d×r矩阵全体,A d,r表示满足下列条件的可测映射α:[0,∞)×Wd-→Rd⊗Rr全体:对任何t≥0,α(t,·)是(Wd,Bt(Wd))到Rd⊗Rr可测的.自然地,我们要求σ∈A d,r,b∈A d,1.这时,X是(Ft)-适应的蕴含着σ(t,X)是(Ft)-循序可测的.当σ(t,X)=σ(t,Xt),b(t,X)=b(t,Xt)时(这时右边的σ:R+×Rd-→Rd⊗Rr,b:R+×Rd-→Rd⊗R),我们称方程是Markov型的.我们在本节考虑的方程都是Markov型的

它的积分形式是

更特别的情形是当σ(t,X)=σ(Xt),b(t,X)=b(Xt)时(这时右边的σ:Rd-→Rd⊗Rr,b:Rd-→Rd⊗R),称方程是时齐Markov型或者型的.

另外我们需要重点解释一下随机微分方程的解的存在唯一性意义,随机微分方程的解要比常微分方程难以理解得多,因为这里还有一个Brown运动.说随机微分方程的解实际上是把方程纯粹看成是一个给出系数函数b,σ的形式.

定义6.1.1　只给定两个函数b,σ如上,随机微分方程(6.1.3)(也称为方程(b,σ))的解是指在某个带有流(Ft)的概率空间(Ω,F,P)上的两个连续适应过程(X,B),满足:

(1)B是Rr上标准(Ft)-Brown运动;(www.daowen.com)

(2)(6.1.4)式成立.

也就是说,概率空间及其上的Brown运动都是解的组成部分,只有系数是给定的.解的唯一性有两种不同的解释.

定义6.1.2　我们说方程(6.1.3)的解有轨道唯一性是指对于给定初值和Brown运动B,从轨道的意义上只有唯一的一个随机过程满足此方程,即若在同一个带流的概率空间上有两个解(X,B)和(X′,B′)且若B=B′,X0= a.s.,则X=X′a.s.另外我们说解有分布唯一性是指两个具有相同初始分布的解X和X′是等价的,即有相同的有限维分布族.通常说的随机微分方程解的唯一性是指分布唯一性.

除了上面所说的解的概念之外,还有一个强解的概念也一样重要.说方程(6.1.3)的解(X,B)是强解,如果X关于B生成的且完备化的流()适应.非强解的解称为弱解.后面叙述的一个重要定理说明,强解存在可以推出方程在概率空间和Brown运动任意给定时有解.实际上,与其说强解是解不如说是一个对应法则,是指任意一个初值和Brown运动对应(至少)有一个解,这时如果有轨道唯一性,那么对应唯一一个解.

下面是随机微分方程的一个简单但著名的例子,它诠释了上面定义中的那些概念,有解但没有强解,有分布唯一性但没有轨道唯一性.例6.1.1　(Tanaka)考虑一维随机微分方程:

其中sgn(x)=1{x≥0}-1{x＜0}.或者说是初值为零的随机微分方程

有下面的结论:

(1)分布唯一性成立,因为解X总是标准Brown运动(由L´evy的刻画定理);

即(W,B)是解;

(3)如果(X,B)是解,那么(-X,B)也是解.因此轨道唯一性不成立;

(4)没有强解.这个的证明比较困难,请参考[10].