3.设X=(Xt)是连续局部鞅且其二次变差过程是确定性的,X0=0,证明:X是Gauss过程.

4.设X,Y是连续半鞅,求乘积XY的协变差过程.

6.设X是连续半鞅,证明:|X|也是连续半鞅,且〈|X|〉=〈X〉.由此如果B是Brown运动,那么

(a)|B|是连续半鞅且它的鞅部分是个Brown运动;

(b)记|B|的连续增过程部分为L,L只在{t:Bt=0}上增加,被称为B在零点的局部时,是由L´evy发现的.

证明.|X|是半鞅实际上已经在上面的习题中证明了,那么

是增过程,其中sgn(x)=1{x＞0}-1{x≤0}是绝对值函数的左导数,因此〈|X|〉=sgn(X)2.〈X〉=〈X〉.如果X是Brown运动,设|B|的鞅部分是M,连续增过程部分是L,那么〈M〉t=〈|B|〉t=〈B〉t=t,因此由L´evy的刻画,M是Brown运动.由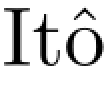公式,B2=|Bt|2=2|B|.|B|+t,因此|B|.|B|是连续鞅,推出|B|.L=0.证明了对几乎所有的轨道,dLt的支撑包含在集{t:Bt=0}中.

7.设M是连续局部鞅,M0=0且〈M〉是确定性的.证明:M是Gauss过程且是独立增量过程.(www.daowen.com)

8.设B是标准Brown运动,X是独立于B的正随机变量.令Mt:=BtX,t≥0.

·B是(Ft)-BM;

·tX是(Ft)-停时;

·自然BtX是连续局部鞅;

·如果X有界,那么Doob定理推出(BtX)是鞅;

再证明〈M〉=tX.