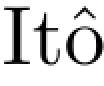公式的第五个应用是鞅表示定理,是最先发现并证明的,它是说关于Brown运动是Brown运动的一个深刻结果.在多维Brown运动场合有一个自然的版本,但这里为了简单起见,我们只考虑一维场合.

特别地,任何Brown流(Ft)t≥0鞅有一个连续修正.

定理的证明依赖于下面的几个引理.设T＞0是任意固定正数.

引理5.2.4　概率空间(Ω,FT,P)上的随机变量集合

在L2(Ω,FT,P)中稠密.

而对任何n,Xn是Gn可测的,那么存在某个Borel可测函数fn:Rn→R使得

引理成立.

如果I⊂R是个区间,那么我们用L2(I)表示I上关于Lebesgue测度平方可积的函数h组成的Hilbert空间.

引理5.2.5　设T＞0.对任何h∈L2([0,T]),定义指数鞅:

在L2(Ω,FT,P)中稠密,其中span表示向量集张成的线性子空间.

证明.只需证明,若H∈L2(Ω,FT,P)使得对任何Φ∈L,有E[H·Φ]=0,那么H=0.

对任何0=t0＜t1＜···＜tn=T与ci∈R,考虑阶梯函数(www.daowen.com)

那么

因为对任何Φ∈L有E[HΦ]=0,故

因为ci都是任意数,故有

对任何ci与ti∈[0,T]成立.显然左边关于ci解析,这个等式对任何复数ci成立.推出对任何实数x1,···,xn有

然后有Fourier变换唯一性推出,对任何φ∈Cb(Rn),

根据引理5.2.4　,形如φ(Bt1,···,Btn)的函数全体在L2(Ω,FT,P)中稠密,故而对任何G∈L2(Ω,FT,P)有

特别地,E[H2]=0推出H=0.

定理5.2.7　()设ξ∈L2(Ω,FT,P),那么存在F=(Ft)t≥0∈L2,使得

证明.由引理5.2.5　,我们只需对于如(5.2.16)中定义的ξ=X(h)T(其中h∈L2([0,T]))证明定理的结论.因为X(h)t是指数鞅故它满足下面的积分方程

因此在这种情形下,我们取Ft=X(h)th(t)就可以了.

现在鞅表示定理5.2.6　从的表示定理与鞅性立刻推出.