现在我们看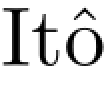公式的第四个应用.固定一个带流的概率空间(Ω,F,Ft,P).设T＞0,Q是(Ω,FT)上关于P绝对连续的概率测度,密度为ξ,即

由定义,对于有界的FT-可测随机变量X

或者简单写成为

其中上标表示关于指定测度的期望.而如果X是Ft-可测的,t≤T,那么

即对于t≤T,

它在概率P下是在时间T之前的非负鞅.

反过来,如果T＞0且Z=(Zt)t≥0是(Ω,F,Ft,P)上初值为1在时间T之前的连续严格正鞅.我们在(Ω,FT)上定义一个测度Q为

也就是说

因为E(ZT)=1,故Q是(Ω,FT)上概率测度.因为Z=(Zt)t≤T是鞅,故对任何t≤T,

练习5.2.5　如果(Zt)t≥0是初值为1的连续正鞅,那么在(Ω,F∞)上存在概率测度Q,其中F∞≡σ{Ft:t≥0},使得对任何t≥0,

下面引理中的结论容易验证,留作习题.

引理5.2.3　(1)一个适应过程X是一个Q-鞅当且仅当XZ是一个P-鞅;

(2)如果XZ是P-局部鞅,则X是一个Q-局部鞅;

(3)在Q测度几乎处处意义下,密度Z总是严格正的.

练习5.2.6　设τ是停时,证明:如果(XZ)τ是P-鞅,那么Xτ是Q-鞅.

我们现在可以叙述并证明Girsanov定理了.

定理5.2.4　(Girsanov)设(Mt)t≥0是概率空间(Ω,F,Ft,P)上在时间T之前的连续局部鞅,(Zt)t≥0是初值为1的连续正鞅,那么

在概率空间(Ω,F,Ft,Q)上在时间T之前是一个连续局部鞅.

证明.应用局部化方法,我们可以假设M,Z,1/Z都是有界的.这时M,Z是有界鞅.我们需要证明X在概率Q之下是鞅,即对s＜t≤T,

也就是说,

由定义

因此我们只需证明(ZtXt)在概率测度P下在时间T之前是鞅.根据分布积分公式,我们有

它显然是一个鞅.

因为Z=(Zt:t≤T)是一个正鞅,我们可以应用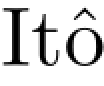公式于log Zt,得到

即Zt=E(N)t,其中

是一个连续局部鞅.因此Zt=E(N)t是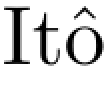积分方程(www.daowen.com)

的解,从而

由此推出

因此我们有下面的推论.

推论5.2.2　设Nt是(Ω,F,Ft,P)上初值为零的连续局部鞅,使得其随机指数

是连续鞅.在可测空间(Ω,FT)上定义概率测度Q:

如果M=(Mt)t≥0是概率测度P下的连续局部鞅,那么

是概率测度Q下和时间段[0,T]上的连续局部鞅.这里读者应该仔细定义时间段[0,T]上的局部鞅的概念.

因为P与Q两个测度等价,所以它们有相同的零概率集.依概率收敛这个性质在两个测度下也是等价的(请自己证明之).

推论5.2.3　设Q关于P等价,则P-连续半鞅X等同于Q-连续半鞅且〈X〉Q=〈X〉P.另外有界循序可测过程H关于X的Q-随机积分与P-随机积分一致.

应用于Brown运动,设F是连续适应过程使得

是鞅,那么在新测度Q下,

是连续鞅,而且它的二次变差过程是t,由Brown运动的鞅刻画推出˜B是新概率测度下的Brown运动.

最后我们说说Girsanov定理的前世.Girsanov定理来源于平移变换后测度的变化这个问题,例如有限维空间上的Lebesgue测度是平移不变的,那么Rd的Gauss测度呢?这很容易,Gauss测度

是Rd上的概率测度,它使得其上的坐标随机变量x是标准正态分布的.对任何y∈Rd

换句话说,Gauss测度经过平移后关于原来的Gauss测度绝对连续,这也称为拟不变性,或者说随机变量xx-y在概率测度

下是标准正态分布的.

在无穷维空间上不存在σ-有限的平移不变或拟不变的测度,但是可以考虑测度沿着某些方向的平移拟不变性.让我们考虑Wiener测度,把Girsanov定理应用于Brown运动就是著名的Cameron-Martin定理,它当然早于Girsanov定理.考虑时间t∈[0,1],设B是把样本映射为样本轨道Bω(t)=Bt(ω),ω∈Ω.设W是[0,1]上初值为0的连续函数全体,μ是W上的Wiener测度,即若f是W上的非负可测函数,则

也可以说,在概率μ之下,坐标过程是Brown运动.

让我们引入Cameron-Martin空间,

那么Girsanov定理说过程˜B=(Bt-h(t):t∈[0,1])在概率Q之下也是Brown运动,即

记W上的平移θh:ww+h,那么即对于W上的非负可测函函数f有

用Cameron-Martin定理叙述如下.

定理5.2.5　(Cameron-Martin)对于h∈H,Wiener测度μ在W上的平移映射θh之下的像关于μ绝对连续,即

或者说沿着Cameron-Martin空间的函数方向平移,Wiener测度有拟不变性.

练习5.2.7　设B=(Bt)是Brown运动.0＜s＜t＜1求条件期望