在本节中,我们考虑简单的随机微分方程

其中Xt=Mt+At是连续半鞅.方程(5.2.1)的解被称为X的随机指数.方程(5.2.1)应该理解为积分方程

其中积分是在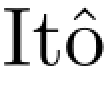积分的意义下.为了找到方程(5.2.2)的解,我们可以试

其中(Vt)t≥0待定为一个有界变差的“修正”项.应用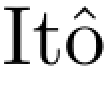公式,我们有

为了满足方程(5.2.2)我们必须让

引理5.2.1　设(Xt)是具有半鞅分解Xt=Mt+At的连续半鞅且X0=0,那么

是方程(5.2.2)的解.

过程E(X)被称为X=(Xt)t≥0的随机指数.

命题5.2.1设(Mt)t≥0是初值为零的连续局部鞅,那么其随机指数E(M)是个非负连续局部鞅.

注释5.2.1　.根据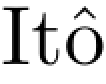积分的定义,对任何T＞0如果

那么随机指数

是非负连续平方可积鞅.

一个重要的事实是尽管E(M)也许不是鞅,但它必定是上鞅.

引理5.2.2　设X=(Xt)t≥0是个非负连续局部鞅且X0可积,那么X=(Xt)t≥0是个上鞅:对任何t＞s≥0,E(Xt|Fs)≤Xs.特别地t→EXt是递减的,因此对任何t＞0,EXt≤EX0.

证明.先证明条件期望的Fatou引理:如果{Xn}是概率空间(Ω,F,P)上非负可积随机序列,那么

其中G是F的子σ-代数(留作习题).

由定义,存在局部化序列{τn}使得Xτn=(Xt∧τn)t≥0是鞅.因此

特别地有

由Fatou引理,Xt=limn→∞Xt∧τn是可积的.应用Fatou引理于Xt∧τn与G=Fs,得

根据定义X=(Xt)t≥0是个上鞅.

显然,一个连续上鞅X=(Xt)t≥0是个鞅当且仅当它的期望t→E(Xt)是常数.因此有下面的推论.

推论5.2.1　设M=(Mt)t≥0是初值为零的连续局部鞅,那么E(M)是个上鞅.特别地,对任何t≥0有(www.daowen.com)

进一步地,E(M)在时间段[0,T]上是鞅当且仅当

局部鞅的随机指数在概率变换中有很重要的地位.在许多应用中,知道一个给定鞅的随机指数是否是一个真正的鞅是一件非常关键的事情.保证(5.2.4)的一个充分条件是所谓的Novikov条件,叙述如下.

定理5.2.1　(Novikov)设M=(Mt)t≥0是个初值为零的连续局部鞅.如果

那么E(M)是一致可积鞅.

证明.下面的证明是严加安给出的(参考[16]).思想如下,先在Novikov条件(5.2.5)下,证明对任何0＜α＜1,

是一致可积的,因此(E(αM)t)是一个鞅,然后再让α↑1.

为了证明一致可积性,对任何给定的α,E(αM)是局部鞅αM的随机指数,故E(αM)是非负连续局部鞅,E(E(αM)t)≤1.我们有下面的性质:

对任何有界停时τ与任何A∈F∞,

从而｛E(αM)τ:τ为有界停时｝有一致绝对连续性,根据定理1.2.4　推出它是一致可积的,因而E(αM)必定是鞅,而且是一致可积鞅.因此记

它满足

在(5.2.7)的第一个不等式中可以取A=Ω与τ=∞,我们将得到下面的不等式:

令α↑1我们将得到

即E[E(M)∞]=1,由此推出E(M)t是一致可积鞅.从定理的证明可以推出,如果对任何t≥0,

那么E(M)是一个鞅,未必一致可积.它可以看成局部Novikov条件.

考虑一个标准Brown运动B=(Bt),且设F=(Ft)t≥0∈L2.如果

那么

是一个[0,T]上的正鞅.

这不是个容易的工作,读者可以作为练习估计它.

如果(Xt)t≥0是非负连续上鞅,那么

再结合指数鞅公式,可以证明下面的指数不等式.

练习5.2.1　设B=(Bt)是标准Brown运动,那么对任何T＞0,