我们在许多场合中应用下面的初等公式

若(Xt)t≥0是个局部鞅,则对j=1,···,n求和,其中0=t0＜t1＜···＜tn=t是任意有限分划,我们得到

让m(D)→0,由定理4.4.6　和定理4.3.2　,右边在依概率收敛的意义下,有

这是对鞅(Xt)t≥0的平方应用It公式.根据极化与局部化以及命题4.4.1,我们便有下面的分部积分公式.它是It微积分中的关键环节.

引理5.1.1　(分部积分)设X与Y是连续半鞅,那么XY是连续半鞅且

注意右边最后的协变差就是它们的局部鞅部分的协变差.这是说连续半鞅空间对于乘积是封闭的,如果X=M+V,Y=N+W是它们的半鞅分解,那么XY的局部鞅部分是X.N+Y.M,它的有界变差部分是X.W+Y.V+〈M,N〉.下面是随机微积分的基本定理.

故而复合的过程f(Xt)还是连续半鞅,它的分解由It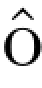公式清晰给出,其连续局部鞅部分是

而其连续有界变差部分为

练习5.1.1　证明:

那么Mf是个局部鞅且

证明.(It公式)我们将证明一维情形当X=M是连续局部鞅时的It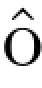公式.应用局部化技术,我们只需要对于连续平方可积鞅M=(Mt)t≥0进行证明.故我们需要证明

下面因为都有下标t,故我们省略之.像我们已经看到的那样,公式对于f(x)=x2(f′(x)=2x,f′′(x)=2)是正确的,

假设(5.1.5)式对于f(x)=xn成立:

则应用分部积分公式于Mn与M,我们得到

这蕴含着(5.1.5)式对幂函数xn+1成立.因此推出It公式对于任何多项式都成立.(www.daowen.com)

例5.1.1　设B=(Bt)是R3上的标准Brown运动,y／=0.h(x):=|x-y|-1,x∈R3\{0},则h(B)={h(Bt)}是局部鞅,但它不是鞅.

首先由(3.4.3)式,单点是极集,也就是说Brown运动的几乎所有轨道都不会碰到y点.对任何k≥1,取

因此h(B)不是鞅.现在h(B)是可积的非负局部鞅,它是上鞅,由Doob的上鞅收敛定理和(5.1.7)式,h(Bt)几乎处处收敛于0,即对于几乎所有轨道,|Bt|趋于无穷,也就是说3-维Brown运动最终会离开任何给定的有界区域.而我们知道直线上的Brown运动是震荡的.

练习5.1.3　证明(5.1.7)式.

下面我们将对随机微积分理论作一个简单的概述.

(1)It积分:关于Brown运动的随机积分.

(2)平方可积鞅的二次变差及其积分理论.

(3)局部化技术:用一列递增趋于无穷的停时列来进行局部化是一个关键的技巧,通过此技巧可以将有界连续鞅的许多结论推广到连续局部鞅情形.

(4)连续局部鞅是鞅的非常重要的推广.非常值的连续局部鞅不可能是有界变差的,积分不能按几乎处处的意义定义.如果M是连续局部鞅,它有二次变差过程〈M〉,这是使得M2-〈M〉是连续局部鞅的唯一连续增过程.

(5)半鞅空间:过程X称为半鞅,如果它是一个连续局部鞅与一个连续有界变差过程的和:X=M+V,这个分解是唯一的,称为半鞅分解.其中的主要角色是连续局部鞅,加上有界变差过程是为了让半鞅空间有很好的封闭性.

(6)半鞅是个线性空间.半鞅有二次变差,它的二次变差等于其鞅部分的二次变差,因为连续增过程的二次变差恒等于零.半鞅之间有协变差,也就是它们鞅部分之间的协变差.

(7)半鞅对乘积封闭,而且有分部积分公式:

(8)半鞅复合一个二次连续可微函数后依然是半鞅,而且有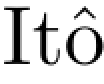公式: