前面关于平方可积鞅的积分理论很漂亮,但是对于过程F和M限制较多.下面我们将It积分扩展至局部有界过程关于连续局部鞅的积分,这非常必要.设M=(Mt)t≥0是初值为零的连续局部鞅,那么我们可以选择停时序列{τn}使得τn↑∞a.s.且对任何n,Mτn=(Mt∧τn)t≥0是初值零的连续平方可积鞅(如果必要,甚至可以是有界的).

设F=(Ft)t≥0是适应过程,且存在停时列{σn},使得σn↑+∞且对任何n,Fσn有界.这时我们说F是局部有界的.显然连续的,或左连右极,或右连左极的适应过程是局部有界的.称为F关于连续局部鞅的It积分.可以证明F.M的定义是无歧义的且不依赖于停时列{˜τn}的选择.事实上,由推论4.4.1　知对任何停时σ≤τ,有

故若t≤˜τn,则

由定义,F.M与

都是初值零的连续局部鞅.而且与定理4.4.3　一样可以证明,F.M是由下面性质刻画的唯一连续局部鞅:对任何连续局部鞅N,有

除了这些,下面这个定理给出了随机积分的控制收敛定理且证明了随机积分仍然是(左端点)Riemann和的极限,但是是依概率收敛的极限.这个收敛定理在证明It公式时也是有用的.

定理4.4.6　设M是连续局部鞅,{F(n)}是在每个t处几乎处处收敛于零的局部有界过程列并且被一个局部有界适应过程F控制,则(F(n).M)在任何有界区间上依概率一致地收敛到零.特别地,如果F是局部有界的左连续适应过程,则对任何t≥0,当[0,t]上的分划D={ti}的长度趋于零时,随机积分(F.M)t是Riemann-Stieltjes和(www.daowen.com)

依概率收敛的极限.

证明.我们先假设F和M是有界过程.这时F(n)∈L2(M)并且由Lebesgue控制收敛定理,它按L2(M)中的度量收敛到零.因随机积分是连续映射,故F(n).M按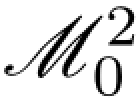中的度量收敛于零,然后由Doob鞅不等式推出(F(n).M)在任何有界区间上依概率一致地收敛到零.

因此

对后一个结论,因为F局部有界左连续,故F是阶梯过程列

的几乎处处收敛的极限,先假设F有界,利用上面的结果证明结论成立,然后再利用局部化方法证明F局部有界时结论也成立.