类似地,我们可以应用定义关于Brown运动的It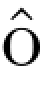积分的过程来定义关于连续平方可积鞅的It积分.关于连续平方可积鞅的积分的定义程序如下:对于连续平方可积鞅M和满足一定可积条件的适应过程F,存在唯一的平方可积鞅,

记为F.M,使得对任何连续平方可积鞅N有

这个刻画非常重要,是联系通常积分和随机积分的纽带.

类似于Brown运动,我们有下面三个重要性质.

为了证明这些性质,先叙述一个引理.

引理4.4.1　设M=(Mt)t≥0是个连续平方可积鞅,s＜t≤u＜v,f∈Fs,g∈Ft,都有界,那么

证明.由条件期望的性质

第二个等式很简单,因为f∈Fs,故可以被移出条件期望,再应用定理4.3.2　知M2-〈M〉是鞅即可.

现在来验证定理的结论.作为例子,我们来证明关键的第二条性质.固定t＞s＞0,如果需要,我们总可以把t,s加入分点中,故设存在j,k使得tk=t,tj=s.由引理得

换句话说,L2(M)是所有简单过程在范数

定理4.4.2　设F∈L2(M),那么

(1)IM(F)∈M20;

(2)(It等距)对任何T＞0,我们有

比上面定理中所说的It等距更一般的是以下定理.

定理4.4.3　设M,N∈M20且F∈L2(M),G∈L2(N).则

唯一刻画性质是显然的.对于(4.4.1)的证明,先假设F,G是简单过程证明之(练习),然后对一般的F,G,取极限分别是F和G的简单过程列F(n)和G(n),那么F(n).M与G(n).N的极限分别是F.M和G.N,因此左边的收敛没有问题,而右边的收敛需要一个著名的不等式,我们将在下一节介绍,定理的证明也要放到下一节.(www.daowen.com)

是鞅,或者说

证明.要证明这个事实,回忆Doob定理说:一个可积过程X是鞅当且仅当对任何有界停时τ有

所以我们需要验证(4.4.6)中的T用有界停时代替也一样成立就可以了,这看上去有点不可能,但实际上因为(4.4.6)是对于所有的连续平方可积鞅N成立,故若取任何有界停时τ≤T,Nτ也是平方可积鞅,应用定理4.3.3　有

尽管(4.4.2)与(4.4.3)等价而且更简单,但我们还是喜欢用后者,因为后者具有可推广性.

如果对任意有界变差过程V,用类似的记号F.V表示积分过程

那么上面的(4.4.2)可以写成为

右边F.〈M,N〉T是指区间[0,T]上F关于〈M,N〉的积分.注意它的左边是随机积分,而右边是通常积分,故它的意义是把随机积分用通常积分来刻画.通过这个刻画,我们可以将许多通常积分的性质搬到随机积分上去.

推论4.4.1　设M∈M20.

(1)若G∈L2(F.M),则G.(F.M)=(GF).M;

(2)若F,G∈L2(M),则(G+F).M=G.M+F.M;

(3)设σ是停时,那么(F.M)σ=F.Mσ=Fσ.Mσ.

证明.显然上面所说的两个性质当M是有界变差过程时是成立的.现在对任何N∈M20,

类似地有

由上面的随机积分刻画定理推出1与3的第一个等号成立,2与3的第二个等号类似证明.