给定概率空间(Ω,F,Ft,P)上的标准Brown运动B=(Bt:t≥0).不妨假设(Ft)满足通常条件.

定义4.2.1　一个适应随机过程F=(Ft)t≥0被称为简单过程(或者阶梯过程),如果它是一个可以表示为如下形式的有界适应过程

其中0=t0＜t1＜···＜ti→∞.

对于上面的简单过程,那么对任何t≥0,只有有限多个ti∈[0,t],另外fi是关于Fti可测的.简单随机过程全体用符号L0表示.如果F=(Ft)t≥0∈L0,那么F关于Brown运动B=(Bt)t≥0的随机积分定义为一个随机过程I(F),

其中上述和式中只有有限多项是非零的.显然I(F)=(I(F)t)t≥0是连续平方可积的且适应于(Ft)t≥0.

引理4.2.1　(I(F)t)t≥0是个鞅,即

证明.设有某个k,j∈N使得tj＜t≤tj+1,tk＜s≤tk+1,那么k≤j且

证明的过程是对各种情形验证鞅性E[I(F)t-I(F)s|Fs]=0.如果k＜j-1,那么

如果k+1≤i≤j-1,那么s≤ti故Fs⊂Fti.因此

第一个等式是由于fi∈Fti,而第二个等式由于(Bt)是个鞅.类似地,

把这些方程放在一起,我们得到

如果k=j-1,那么tj-1＜s≤tj＜t≤tj+1且

我们因此有

引理4.2.2　随机过程

也是一个鞅.

证明.我们想要证明对任何t≥s,

换句话说,我们需要证明

显然

因为(I(F)t)t≥0是个鞅,故

但是I(F)s∈Fs,故有

我们因此需要证明

我们现在使用引理4.2.1　的证明中所用的相同符号.由(4.2.2)容易看出如果k＜j-1,那么

利用引理4.4.1　以及(Bt)t≥0与(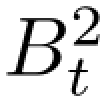-t)t≥0都是鞅的事实,我们得到

因此如果F是一个简单过程,那么It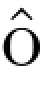积分I(F)是个初值为零的连续平方可积鞅,F→I(F)是线性的,且对任何t≥0,

等式(4.2.3)称为It等距,它是我们定义随机积分的关键.下面我们把随机积分的定义扩展到简单过程的极限.

为了把It积分的定义扩展到更大类的被积过程类,首先我们需要引入两个重要的空间.设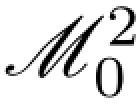是连续的平方可积(Ft)-鞅过程M=(Mt:t≥0)全体,这个空间的距离有两种定义方式,一种定义方式是赋可列范

这个不是真正的范数;另外一种定义方式是把其中满足supt＞0 EM2t＜∞的连续鞅拿出来,定义

这种方式更干净一点,但条件太强,Brown运动也不满足这个条件,也不是很好.我们这里采用折中的方式,考虑对任何T＞0,时间集为[0,T]上的连续平方可积鞅M=(Mt:t∈[0,T]),

由鞅的性质,如果||M||M2=0,则M在[0,T]上恒等于零a.s.,因此||·||M2是M20上的范数,容易看出它实际上是由内积诱导的.在下面的定理与叙述中,T是任意固定的数.

定理4.2.1　连续平方可积鞅空间M20是Hilbert空间.(www.daowen.com)

这显然是L0上的一个由内积诱导的范数,用L2表示L0的关于||·||L2的完备化空间,是一个Hilbert空间.

如果过程F=(Ft)t≥0是简单适应过程序列{F(n):n∈N}当n趋于无穷的极限

那么Ito积分的线性性质与It等距蕴含着

是鞅.

练习4.2.1　证明以上定理中最后一句话.

尽管L0看上去不大,但完备化之后的被积过程空间L2是一个很大的空间,下面的引理给出一个充分条件,对我们来说已经足够了.

引理4.2.3　设F=(Ft)t∈T是适应且左连续随机过程,满足

那么F∈L2且依概率有

其中极限是对于[0,t]所有有限分划取的.

证明.显然L2的有界过程全体在其中稠密(请验证),故我们不妨设F有界.对于n＞0,设

是[0,T]上一个有限分划序列使得当n→∞时,

令

由定义得F∈L2.

注释4.2.1　.条件F=(Ft)t≥0适应于由Brown运动生成的流(Ft)t≥0,在定义It积分时是本质的.而另一方面,过程t→Ft的左连续性是技术性的,它可以被其它可测性代替.当定义F=(Ft)t≥0相对于具有不连续点的鞅的随机积分时,其左连续性变成是必需的.理由是F在时刻t的左极限在时间t之前“发生”,如果t→Ft左连续,那么,对任何时间t,Ft的值可以被时刻t之前的值所预测

注释4.2.2　.我们应该指出某种形式的联合可测性(t,ω)→Ft(ω)是必要的,以保证(4.2.5)有意义.注意到(4.2.5)可以写成为

故自然的可测条件应该是对任何t＞0,函数

作为[0,t]×Ω上的函数关于B([0,t])⊗Ft可测,其中B([0,t])是[0,t]上Borel σ-代数.这实际上就是随机过程关于给定流的循序可测性.

练习4.2.2　设B=(Bt)是适应的Brown运动.证明:对任何Borel可测函数f使得

那么(f(Bt))t≥0是在L2中.

条件(4.2.8)究竟是什么意思呢?实际上

其中

因此当α≤0时,

当α＞0时,

练习4.2.3　设f是[0,T]上的绝对连续函数.证明:

注意右边是通常积分.

如果F=(Ft)t≥0∈L2,那么下面两个过程

是初值为零的连续鞅,特别地

且对任何t≥s,

至此,It的关于Brown运动的随机积分被完美地定义了,其中的关键是It等距,而It等距的关键是Brown运动有两次变差过程.也就是说,如果我们想对一般的平方可积鞅定义随机积分,必须要先讨论它是否具有二次变差过程.