设B=(Bt)t≥0是完备概率空间上关于流(Ft)的d-维标准Brown运动,其自然流加入所有零概率集后的流记为(Ft).下面是Brown运动的分形性质.

引理3.4.1　对任何实数λ／=0,

是Rd上标准Brown运动.

此结论可由Brown运动的定义直接推出.特别地,(-Bt)t≥0也是标准Brown运动.下面是Brown运动的旋转不变性.

引理3.4.2　若U是d×d正交矩阵,那么UB=(UBt)t≥0是Rd上标准Brown运动.也就是说,Brown运动在正交变换下是不变的.

为了证明下面一个性质,介绍Brown的另外一个刻画.设B=(Bt)t≥0是R上标准Brown运动,那么B是中心化Gauss过程,其协方差函数为C(s,t)=s∧t.事实上,首先B的任何有限维分布都是Gauss分布,且EBt=0,故B是中心化Gauss过程,算其协方差函数,对s＜t,

反过来也不难验证,留作习题.下面是Brown运动的一个有用的刻画.

定理3.4.1　一个连续的中心化Gauss过程(Xt:t≥0),具有协方差函数

是标准Brown运动.

下面是Brown运动的时间逆转不变性.

引理3.4.3　如下定义的过程

是R上标准Brown运动.

证明.显然Mt是中心化Gauss过程且其协方差函数为

与Brown运动一致,所以我们只需证明(Mt)连续就可以了,这里的关键就是证明M在t=0时连续,即limt↓0 tB1/t=0 a.s.

事实上,M与B有相同的有限维分布,根据Brown运动的构造定理,存在M的一个连续修正,记为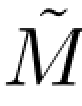,因为M在(0,∞)上是连续的,故M与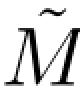在(0,∞)上是恒等的,因此limt→0 Mt=limt→0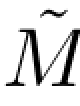t=0.

另一个证明limt→0 Mt=0的简单方法是应用Doob的鞅不等式.由鞅不等式

由Borel-Cantelli引理推出当n→∞时,有

这蕴含有Mt→0 a.s.

这实际上已经证明了所谓的Brown运动的强大数定律.

定理3.4.2　设B=(Bt)是标准Brown运动,则

现在我们证明Brown运动有Markov性.

让n趋于无穷,由Brown运动连续性推出(3.4.1).

定理实际上是说(Bt+T-BT:t≥0)是一个与FT+独立的标准Brown运动,由此推出

其中Ptf(x)=E[f(Bt+x)].这就是重要的强Markov性:给定现在,将来与过去独立.

练习3.4.1　利用上面的强Markov性证明:对于固定时间t有Ft=Ft+.也就是说,只要在Brown运动的自然流中加入零概率集,它将自然满足通常条件.

反射原理是远比Markov性质更为经典的一个概念.我们将应用这个原理来计算Brown运动的极大游程的分布.在许多应用实例中,特别在统计中,我们需要估计随机过程的极大游程的分布.对于Brown运动B=(Bt)t≥0来说,极大游程sups∈[0,t]Bs的分布可以由反射原理的方法来导出.设B=(Bt)是标准Brown运动.固定一个时间t＞0,让Brown运动在时间s之后依Bs反射,即令

反射原理当s是停时时也成立.设b＞0与b＞a,并设

那么Tb是停时,定义Tb处的反射

其中第一个等式直观上是说Brown运动在Tb之后开始算实际上是一个从b出发的Brown运动,所以它关于y=b是对称的,就如同标准Brown运动关于原点对称.第二个等式就是这对称性的推论.也就是所谓的反射原理.上面的方程可以写成为

关于反射原理的严格证明要用到Brown运动的强Markov性.

由反射原理(3.4.2)可得

它给出了Brown运动与其极大游程的联合分布.

特别地,当a=b＞0时,有

它的密度函数为

练习3.4.3　证明:当b／=0时

公式P(Tb＜∞)=1意味着Brown运动肯定可以在有限时间内命中任何一点b,这在直观上是显然的,因为它的轨道连续而且会在-∞到+∞之间震荡.但是这个性质与维数有关,2-维以上的Brown运动就不大可能还可以命中一个给定的点.确切地说,如果B是d-维Brown运动,d≥2,x∈Rd,那么

其中Tx是{x}的首中时.这时我们说,对于多维Brown运动,单点是极集.这是1-维与多维之间的巨大区别.

上面的计算依赖于b＞0.零点的首中时T=T0又会怎么样呢?

练习3.4.4　对于每个连续轨道的样本ω,证明:b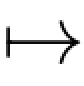Tb(ω)是左连续的.

这个练习说明不能用让b趋于零的方法来解决问题.我们需要应用另外一个技巧,对t＞0,令

即时间t之后首次命中0的那个时刻.显然Tt↓T.因为X=(Bs+t-Bt:s＞0)是独立于Bt的标准Brown运动,故Tt等于t加上X首中-Bt的时间,也就是说,(www.daowen.com)

让t趋于零推出E[e-sT]=1,即P(T=0)=1.

练习3.4.5　(*)Brown运动几乎每条样本轨道的零点集合是Lebesgue测度为零的无孤立点的闭集.

下面考虑鞅性.

定理3.4.4　(1)一维Brown运动(Bt)t≥0是连续平方可积鞅;

也就是说,(Bt)t≥0是连续鞅.

(2)这里只考虑i=j,显然我们只需对一维Brown运动证明.这种情形下,

这已经证明了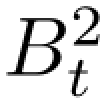-t是一个鞅.情形i／=j留给读者.

下面定理用特征函数唯一性的角度来看是显然的.

定理3.4.5　 Euclid空间Rd上从0点出发适应于某个流(Ft)的连续随机过程B=(Bt)是标准Brown运动当且仅当对任何ξ∈R与t＞s

推论3.4.1　设(Bt)是Rd上标准Brown运动.如果ξ∈Rd,那么

是鞅.

注释3.4.1　.注意到(3.4.4)的两边都是ξ的解析函数,故等式对任何复值ξ也成立.特别地,用-iξ代替ξ,我们得

因此对任何向量ξ,

是一个连续鞅.这个结论也可以推广到Rd上的向量场ξ=(ξ(t)),由此得到的等式被称为Cameron-Martin公式.

让我们利用Brown运动的鞅性质以及Doob定理来解决一些问题.

例3.4.1　设B=(Bt)是1-维标准Brown运动.对a＞0,定义Ta是B到点a的首中时,那么它是停时,前面用反射原理证明了Brown运动一定会到达a,即

我们也可以用鞅方法来解答这个问题.更一般地,我们问Brown运动会肯定碰到一条斜的直线x=kt-a吗?令T是Brown运动B首次碰到这条直线的时间,即

这也可以说是漂移Brown运动(Bt-kt)首次碰到-a的时间,求P(T＜∞).不妨设a＞0,当k=0时,T=T-a.直观看,当k＞0时,P(T＜∞)=1,而当k＜0时未必.

由指数鞅性质,对任何实数z,

是鞅.由Doob定理,

让t趋于无穷,问题的关键是极限与期望是否可以交换.当z＜0时,

因此要保证(3.4.5)式中的指数关于t,ω有界,必须zk-z2/2≤0.需分两种情况,一种是k≥0,这时只要z＜0;另外一种情况是k＜0,这时只要z＜2k.无

论哪种情况,都可以应用有界收敛定理,

这时BT=kT-a,因此

在第一种情况下,可以让z↑0,得P(T＜∞)=1;在第二种情况下,让z↑2k,得

在第一种k≥0情况下,我们可以算出T的Laplace变换,因为

如果用Ta表示上面的T,那么(Ta:a≥0)是一个平稳独立增量过程,称为相对稳定过程.

例3.4.2　设a＜0＜b,Ta,Tb分别是原点出发的Brown运动首次碰到a,b的时间.用鞅方法来求P(Ta＜Tb),E[T]以及T的Laplace变换,其中T=Ta∧Tb.由鞅的期望不变性,对任何t＞0,

当t→∞时,a≤BT∧t≤b,因此由控制收敛定理得EBT=0.而

因此aP(Ta＜Tb)+bP(Tb＜Ta)=0,即

要算ET,需要用鞅(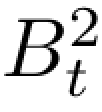-t),还是由期望不变性,

然后让t→∞,左边应用控制收敛定理右边应用单调收敛定理得

类似地,要算T的Laplace变换,应该用指数鞅(exp(λBt-λ2t/2)).由期望不变性和控制收敛定理得

因此

从上面两个方程推出

其中sinhx=(ex-e-x)/2.由此立刻得到T的Laplace变换.

Brown运动是L´evy过程的基本例子,L´evy过程是Euclid空间上的右连续平稳独立增量过程,(3.4.4)式是关于Brown运动的L´evy-Khinchin公式.一般地,如果(Xt)是一个d-维L´evy过程,那么对t＞s与ξ∈Rd,

其中ψ是连续复值函数,被称为L´evy指数,它唯一地决定L´evy过程.L´evy指数有下面的表达式,称为L´evy-Khinchin公式:

这里S是一个d×d对称非负定矩阵,b∈Rd,而ν是Rd上负荷在原点外的σ-有限测度,称为X的L´evy测度,它满足下列可积条件: