1.设(Yn:n≥1)是一个具有有限状态空间E的Markov链,P=(p(x,y)):x,y∈E是转移矩阵,即对任何n≥1及y∈E,有

α:E→R是P的从属于特征值λ的特征向量:Pα=λα.令Xn:=λ-nα(Yn),证明:(Xn:n≥1)是一个鞅.

2.设X是零均值平方可积的独立增量过程,证明:存在唯一的T上初值为零的递增函数F,使得(X2t-F(t))是一个鞅.

3.(Wald鞅)设{Yn:n≥1}是独立同分布随机序列使得φ(t):=E[etYn]对某个t／=0有限.令

证明:{Xn:n≥1}是鞅.

4.一个袋子中在时刻0有一个红球与一个白球.随机地从袋子中取一个球,然后将它放回并放入一个相同颜色的球,无限地重复此过程.记Xn为n次后袋中白球数与总球数之比.证明:{Xn}是鞅.

5.设{Yn:n≥1}是独立同分布随机序列,f0,f1是两个概率密度函数,f0＞0.令

证明:如果f0是Yn的密度函数,那么(Xn)是鞅.

6.设{Xn:n≥0}是(Fn)适应的可积随机序列,满足

其中α＞0,β＞0,α+β=1.问a为何值时,序列Y0:=X0,Yn:=aXn+Xn-1是(Fn)鞅?

7.设Markov链{Xn:n≥0}的状态空间为{0,1,···,N},转移概率为

8.设{Yn}是独立同分布正随机变量序列使得EYn=1.记Xn:=Y1Y2···Yn.

(a)证明:(Xn)是鞅且几乎处处收敛于一个随机变量X;

(b)设Yn以概率1/2分别取值1/2与3/2.验证X=0 a.s.因此

9.(Doob分解)证明:下鞅(Xn)可唯一分解为Xn=Yn+Zn,其中(Yn)是鞅,(Zn)是从0出发的非负可预料的增过程:0=Z1≤Z2≤···.

10.(Riesz分解)证明:上鞅(Xn)可分解为Xn=Yn+Zn,其中Y是鞅,Z是位势(即Z是上鞅且limn EZn=0)当且仅当{EXn}有界.这时此分解唯一.

11.设{Xn}是鞅且|X0(ω)|,|Xn(ω)-Xn-1(ω)|被一个与ω及n无关的常数控制.如果τ是一个具有有限均值的停时,证明:Xτ可积且EXτ=EX0.

12.设{Xn:n≥0}是例2.1.4　中定义的从a出发的随机游动,τ是首次到达{0,b}的时间.证明:当p=q时,X2n-n是鞅.并由此求Eτ.

13.设{Xn:n≥0}是例2.1.1　说的随机游动,p＞q.取整数b＞0,令σ:=min{n:Xn=b}.求停时σ的母函数并由此计算σ的均值与方差.

14.设ξ1,ξ2,···,ξn,···是独立同分布可积随机变量.对k≥1,令Sk:=ξ1+···+ξk,证明:{···,Sk/k,Sk-1/(k-1),···,S2/2,S1}是鞅.由此证明Kolmogorov强大数定律.(www.daowen.com)

提示.只需证明

就足够了.

15.如果X是非负上鞅,那么

16.设{Xn:n≥0}是鞅,τ是停时.如果

(a)P(τ＜∞)=1;

(b)E|Xτ|＜∞;

(c)limn E[Xn;{τ＞n}]=0;那么E[Xτ]=E[X0].

(a)P(|Xn|＞A)收敛;

18.设X是一个(Ft)适应的,右连续并具有左极限的过程.令A是使得X在[0,t)上连续的样本全体.证明:A∈Ft.

证明.令Yt=(Xt-,Xt),当然Y=(Yt)也是(Ft)适应的.定义

其中d是状态空间E×E的对角线,那么τ是开集的首中时,故是(Ft+)-停时,因此A={τ≥t}={τ＜t}c∈Ft.

19.设τ是个停时,σ是随机时间且σ≥τ.证明:如果σ是Fτ可测的,则σ是个停时.

21.设τ,σ是(Ft)停时,则Fτ∧σ=Fτ∩Fσ,且事件{τ＜σ},{τ≤σ}∈Fτ∩Fσ.

22.(F¨ollmer引理)设X=(Xt:t∈T)是一个下鞅,D是T的一个可列稠子集,对正整数K＞0,令DK:=[0,K]∩(D∪{0,K}),则

(a)对几乎所有的ω∈Ω,从D到R的映射t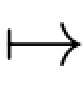Xt(ω)对任何K＞0在DK上是有界的且在每个点t∈T有右极限

及左极限

序列sn↑↑t表示对任何n≥1,sn＜t且sn↑t.↓↓类似理解;

23.设(Xt)是一个关于(Ft)的右连续非负上鞅.证明:当t→∞时,Xt几乎处处收敛于一个可积随机变量,记为X∞,且(Xt:0≤t≤+∞)是(Ft)上鞅.

24.证明:一个鞅是一致可积鞅当且仅当它是右闭鞅(Doob鞅).