后面我们将考虑连续时间鞅,虽然本质上连续时间与离散时间理论没有太大的区别,但是在技术细节上连续时间理论要复杂一些,连续时间鞅论是法国以P.A.Meyer领导下的Strassburg学派培育和发展起来的,他们将Doob的鞅论和It的随机积分理论结合起来发展出了现在所谓的随机分析理论.

如果说前面我们所讨论的概率论与随机过程部分都还没有完全脱离测度论的框架,则下面将引入的停时的概念已完全超越了测度论的范畴.停时是经典随机过程理论中最能体现概率直观背景的概念之一.可以说,没有停时的讨论,就不能称为随机分析.设有概率空间(Ω,F,P)和T⊂R.回忆F的子σ-代数族(Ft:t∈T)称为流,如果对任何s＜t,有Fs⊂Ft.因为加入所有零概率集及其子集到每个Ft中不会影响条件期望,所以我们总是假设每个Ft中含有零概率集及其子集.对任何t∈T,定义那么(Ft+)也是流.一个流(Ft)称为是右连续的,如果对任何t,Ft=Ft+.连续情况下停时的定义类似于离散时间.

定义2.2.1　给定概率空间(Ω,F,P)及流(Ft),映射τ:Ω-→T∪{∞}称为是一个(Ft)停时,如果对任何t∈T,{ω∈Ω:τ(ω)≤t}∈Ft.

停时是相对于一个流而言的,但当上下文明确时,就简单地说一个停时.(Ft)停时必是(Ft+)停时.

练习2.2.1　证明:τ是(Ft+)停时当且仅当对任何t,有{τ＜t}∈Ft.设τ是(Ft)停时,定义

直观上表示τ之前的信息.

练习2.2.2　证明:

1.Fτ是一个σ-代数;

2.τ是Fτ可测的;

3.如果τ≡t时,Fτ=Ft;

4.一个随机变量ξ是Fτ可测当且仅当对任何t∈T,ξ·1{τ≤t}是Ft可测的.

引理2.2.1　设τ,σ,τn是(Ft)停时.

(1)τ∨σ,τ∧σ是停时;

(2)当τn单调上升时,limτn是停时;

(3)当τn单调下降且(Ft)右连续时,limτn是停时;

(4)如果σ≤τ,则Fσ⊂Fτ;

证明简单,留作习题.

先引入连续时间随机过程.直观地说,依时间记录的随机变量族即是随机过程.设T=[0,∞),当然可以是任意的区间.

定义2.2.2　设(Ω,F,P)是一个概率空间,(E,E)是一个可测空间,一个取值在E上的可测映射族X=(Xt:t∈T)称为是(Ω,F,P)上以(E,E)为状态空间的随机过程.

在本书中,所谓的状态空间E通常取为Euclid空间Rd,当d=1时相应的过程称为实值过程.为了方便,我们使用几个几乎自明的概念:可积过程,一致可积过程以及平方可积过程.按照随机过程的定义,随机过程的例子随手可得,我们将在下面的例子中介绍一些重要的被关注的随机过程.对于随机过程来说,有几个重要的概念需要了解,实际上也是概率论的语言.首先是样本轨道,我们知道Ω称为样本空间,点ω∈Ω称为样本点,当样本点ω固定,Xt(ω)作为t的函数是T到E的映射,称为是样本轨道.例如,记录在一个重复掷硬币试验中正反面的结果是一个样本轨道;随时间记录的某个股票的价格可以看成为是一条样本轨道;随时间记录的长江水位也是一条样本轨道;观察花粉在液体表面的运动给出一条轨道,不同的花粉可以看成为不同的样本轨道;记录某人在一个赌局中赌资的变化也是样本轨道.随机过程的概率也就是样本轨道的分布情况.

定义2.2.3　称随机过程X是连续的,如果其几乎所有样本轨道是连续的,即存在一个零概率集N使得当ω／∈N时,t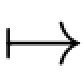Xt(ω)是连续的.右连续与左连续的概念可以类似定义.

首中时的定义与离散时间类似.给定状态空间为E的随机过程X=(Xt),对A⊂E,ω∈Ω,定义A的进入时和首中时如下:(www.daowen.com)

空集的下确界总是定义为无穷,因此TA＜∞当且仅当对某个t有Xt∈A.进入时与首中时的区别在于过程的初始位置,若轨道的起始点不在A中,则DA=TA;若轨道从A中的点出发,则DA=0而TA不一定.在随机过程理论中,首中时用得更多一些.前面我们看到,离散时间情况下证明首中时是停时几乎是平凡的,连续时间的情况要复杂得多,这里我们只考虑开集或者闭集的首中时.

例2.2.1　设X是关于流(Ft)适应的以度量空间(E,d)为状态空间的随机过程.我们先证明若A是闭集且X是连续过程,则DA是(Ft)停时.事实上,这时由轨道的连续性DA≤t当且仅当

但是X的轨道只是几乎处处连续的,因此{DA≤t}与Ft可测集

只相差一个零概率集,也就是说如果Ft包含了所有零概率集,那么{DA≤t}∈Ft,即DA是(Ft)停时.为了证明闭集的首中时TA也是停时,对任何n,令

那么DnA也是停时且单调递减趋于TA,因此,如果流(Ft)是右连续的,那么TA也是停时.也就是说,当随机过程连续,适应流包含零概率集且右连续时,闭集的首中时是停时.显然,如果随机过程是右连续而不是连续时,上面的方法就不能用了.

开集的情况略微容易一些,若A是开集且X是右连续的,那么在右连续的轨道上,TA＜t当且仅当存在有理数s＜t使得Xs∈A,因此若Ft包含所有零概率集,则{TA＜t}∈Ft,即TA是(Ft+)-停时,但一般不是(Ft)-停时.直观地,X的一条轨道t时刻(包括t)前的信息不能告诉我们它是否将立刻进入一个开集.也就是说在(Ft)包含所有零概率集及其子集且右连续的情况下,我们可以证明开集的进入时和开集的首中时是停时.

从这个例子可以看出,要使得一个闭集或者开集的首中时是关于流(Ft)的停时,需要的条件是流(Ft)有右连续性且它们都包含有所有零概率集,这正是所谓的通常条件.

引理2.2.2　设流满足通常条件.那么一个连续适应过程关于开集或者闭集的首中时是停时.

这里我们可以看出在连续时间情况下证明首中时是停时不是像离散时间情况那么简单和平凡.为了它是可测的,随机过程本身需要有某种联合可测性.

与停时密切相关的是停止位置Xτ,首先要讨论它的可测性问题,为了它是可测的,随机过程本身作为二元函数要有某种联合可测性,适应性只是随机过程固定时间时候的可测性,不是联合可测性.其实这也是与Borel集的首中时是否是停时密切相关的概念,但我们不想在这个问题上深入探究.对随机时间τ:Ω→T∪{+∞},自然地定义

注意,此映射的定义域是{τ＜∞},除非X+∞处处有定义.当τ是A的首中时时,Xτ是首中点.再定义X的τ停止过程(或局部化过程)为

停止过程是连续时间鞅论中所使用的主要技巧之一.

定义2.2.4　设T=[0,∞),X=(Xt)t∈T是以拓扑空间E为状态空间的(Ft)t∈T适应过程,称过程X是可测的,如果映射(s,ω)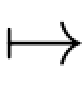Xs(ω)是从(T×Ω,B(T)×F)到(E,E)的可测映射;称X是(关于流(Ft))循序可测的,如果对任何t∈T,映射(s,ω)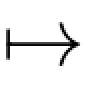Xs(ω)是从([0,t]×Ω,B([0,t])×Ft)到(E,E)的可测映射.

循序可测过程是介于适应过程和右连续适应过程之间的一个概念.

定理2.2.1　如果流(Ft)包含所有零概率集,那么一个右连续(或左连续)的(Ft)

适应实值过程是循序可测的.

证明.对t∈T,n≥1,令

下面我们证明Xτ实际上是关于Fτ可测的,这个结论非常重要.

定理2.2.2　如果X是以E为状态空间的(Ft)循序可测过程,τ是(Ft)停时,则Xτ限制在Ωτ:={τ＜∞}上是(Ωτ,Fτ∩Ωτ)到(E,E)的可测映射.

证明.因X是循序可测的,故对任何t∈T,(s,ω)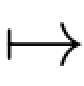Xs(ω)是从([0,t]×Ω,B([0,t])×Ft)到(E,E)的可测映射.而容易验证ω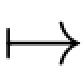(τ(ω)∧t,ω)是(Ω,Ft)到([0,t]×Ω,B([0,t])×Ft)的可测映射,因此两个映射的复合ω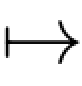Xτ(ω)∧t(ω)是(Ω,Ft)到(E,E)的可测映射,那么对任何B∈E,{Xτ∈B}∩Ωτ∩{τ≤t}={Xτ∈B,τ≤t}={Xτ∧t∈B}∩{τ≤t}∈Ft,即{Xτ∈B}∩Ωτ∈Fτ.

实际上,循序可测性的重要性远比此处显示的要大,例如如果流满足通常条件,那么一个循序可测过程关于任何一个Borel集的首中时是停时,不仅限于开集闭集.本书后面没有用到这个一般性结果.