在本节中,我们将着重介绍鞅的定义及一些常用的例子.简单地说,鞅就是公平原则.在生活中有许多无法预见结果的事件,如比赛,掷骰子,下一个看见的汽车是单号还是双号等.人们可以在任何这样的事件上进行下注赌博,只要进行赌博的各方认为规则是公正的.公正的基本思想是:风险与可能的获利成正比.比如买彩票,中奖的概率极微,但一旦中奖,奖额极大,人们在这里买的是运气,而不是概率.又如将钱存入银行,当然一般不会血本无归,但一般获利也仅是利息而已.这就是鞅的基本思想.在本章中,我们从离散时间鞅开始,离散时间鞅比较直观,它的基本框架是Doob建立的.

给定概率空间(Ω,F,P),设{Fn:n≥0}是F的子σ-代数列且高于n递增,通常称为是一个信息流,表示信息随着时间的增加而增加.我们说一个随机过程X=(Xn)是关于(Fn)适应的,如果对任何n,Xn关于Fn可测,这时也说(Fn)是X的适应流.信息流并不神秘,任意给定一个随机过程X=(Xn),它自然地给出一个(信息)流

它是X适应的最小信息流.信息流这个概念对于理解随机分析特别重要,在后面连续时间的情况下将进一步阐述.

定义2.1.1　一个可积的实值过程X=(Xn)称为是关于(Fn)的鞅,如果X是(Fn)适应的且对任何n,有

如果对任何n,有

称X是下鞅.

鞅与流有关,关于大的适应流是鞅蕴含着关于小的适应流也是鞅.所以一个鞅关于其自然流总是鞅.为了简单起见,当一个流给定后,我们所说的适应以及鞅等概念都是相对于给定信息流而言的.如果预先未指定一个流,鞅就是指关于此过程的自然流的鞅.称X是上鞅,如果-X是下鞅.我们通常仅需关注鞅与下鞅,上鞅的性质可以从下鞅导出.直观地,对于一个鞅来说,以到现在为止的信息来预期将来某时刻的输赢是不可能的,或者说,至多能知道将来的输赢关于现在的条件期望是零.由定义,立刻得到下列简单性质:

(1)鞅的全体是线性空间;

(2)鞅的期望EXn关于n不变.下鞅的期望EXn关于n递增;

(3)由Jensen不等式,如果X是鞅,φ是凸函数,那么若φ(X)可积,则是下鞅.因此|X|,X2(若X平方可积)是下鞅.另外,如果X是下鞅,φ是下凸递增函数,那么φ(X)也是下鞅.因此X+是下鞅.

因此当p=q时,X就是Z上简单随机游动,是个鞅;当p≥q时,X是下鞅;当p≤q时,X是上鞅.可以看出鞅对应于一个对双方公平的博弈对局,而下鞅与上鞅分别对应于一个对己有利与对他有利的博弈对局(按此结论,也许把上鞅与下鞅的名称对换一下更适合实际的意义).

鞅论是从Doob的基本定理开始的,设(Ω,F,P)是概率空间,(Fn:n≥0)是流.一个随机序列{Hn:n≥1}称为是可预料的,如果对任何n≥1,Hn是Fn-1可测的.设X是适应过程,Hn是可预料过程,定义一个初始值为Y0的随机过程Y=(Yn)满足

称为是过程H关于X的随机积分,它是一般随机积分的离散形式(为了在符号上区别乘积与随机积分,除非必须,我们写乘积时一般不用点).

例2.1.2　随机积分有非常直观的解释.考虑市场上有一个价格为S=(Sn:n≥

0)的风险资产和利率为r的债券以及一个持有初始资产X0的投资人的财富过程.一个投资策略是指在时刻n-1决定第n时段持有Hn份风险资产,剩下的资金购买债券,即n-1时刻的资产总额为

那么其投资组合在时刻n的价值为

由此推出

两边同乘以(1+r)-n得

也就是说,折现后的财富过程{(1+r)-nXn}是投资策略{Hn}关于折现后的资产价格过程{(1+r)-nSn}的随机积分.

用H.X表示H关于X的随机积分.下面这个定理称为Doob的鞅基本定理,它是整个随机分析的第一块基石,重要性无与伦比.

定理2.1.1　设X是一个适应过程,H是可预料过程使得H.X是可积的.如果X是鞅,那么过程H.X是鞅.如果X是下鞅且H非负,那么H.X是下鞅.

证明.显然H.X是适应的,且对n≥1,

因此X是鞅(对应地,X是下鞅及H的非负性)蕴含着H.X是鞅(对应地,下鞅).

称H是局部有界,如果对任何n,Hn是有界的.不难证明,如果X可积,且H局部有界,那么H.X是可积的.Doob的鞅基本定理有直观的解释,定理上面的例子已经告诉我们随机积分的直观意义,那么这个定理就是说如果折现后的资产价格过程是一个鞅,那么不管什么样的投资策略得到的财富过程还是鞅,从概率的角度看不会更好也不会更坏.这实际上是生活的常识,我们大多数人也许在日常生活中会感应到这种道理,所以每当笔者看到这个定理时,内心会感叹Doob对于生活常识的那份洞察力和抽象能力.

现在我们需要引入停时的概念,它是随机分析最重要的概念之一.

定义2.1.2　停时是一个值域为随机过程时间集(可以取∞)的随机变量τ,满足对任何n有{τ≤n}∈Fn.这样的停时也称为(Fn)-停时.如果τ是停时,定义Fτ是满足对任何n有A∩{τ≤n}的事件A的全体.

如果把随机时间理解为某件事情发生的时间,那么停时的意思就是这件事情是否在n时刻前发生可以由n时刻前的信息来判断.特别地,确定性的时间是停时.

最典型的停时是首中时,设X=(Xn)是关于流(Fn)适应的随机序列,定义

称为是集合A⊂R的首中时.当A是Borel集时,有

所以τ是首中时.停时是随机过程理论最直观和自然的概念,它的引入对于随机过程研究的意义是非同寻常的,本来随机过程或者概率论还离不开测度的框架,但停时的引入使得随机过程有了自己专注的问题.举两个非停时的例子.

例2.1.3　 X如上,对A⊂E,ω∈Ω,定义

LA是轨道最后一次在A中的时间,称为是A的末离时.一般地LA不是停时,因为轨道在n时刻后不再进入A这样的事件{LA≤n}不能只用轨道在n时刻前的信息来判断.

另外一个时间在股市上经常会遇到,比如人们期望在股票价格最低时买入最高时抛出.让N＞0固定,

这个时间不是停时,因为在任何时候都无法判断前面的某个时刻随机过程是否达到了整个时间段的最大值.差别是如果你计划在股票价格达到某个高度时抛出,那么这个计划是可行的;但如果你计划在股票达到最高点时抛出,那么这个计划是不可行的.这就是停时与非停时的重要区别.

下面练习中的性质很重要,但容易验证.

练习2.1.2　如果τ,σ是停时,那么取小τ∧σ也是停时.

有停时,就有停止位置,Xτ就是τ时刻X所处的位置,也就是说,

或者说当τ=n时,Xτ=Xn,实际上Xτ只能定义在Ω的子集{τ＜∞}上.作为一个特例,设τ是停时,容易验证下面的恒等式

其中的Hn:=1{τ≥n}=1-1{τ≤n-1}是Fn-1可测的且有界的.回忆上面定义的停止过程Xτn:=Xτ∧n,我们得到下面的Doob有界停止定理.

定理2.1.2　(Doob)设X是一个鞅,τ是一个停时,则τ停止过程Xτ也是一个鞅.因此如果τ是有界停时,那么

定理2.1.3　(Doob)设X是一个下鞅,σ,τ是有界停时且σ≤τ,则Xσ,Xτ是可积的,且有

当X是鞅时,等号成立.

练习2.1.3　(1)证明定理2.1.3　;(2)设X是可积适应过程,如果对任何有界停时σ≤τ有

证明X是一个下鞅且

Doob停止定理是研究与停时相关问题的重要工具,让我们从随机游动及其首中时开始.下例是Doob停止定理的一个经典的应用.

例2.1.4　设{ξn}是一个一维格点上的随机游动,即它是独立随机序列且

令X0=0,

它是从0出发的随机游动.对a＞0,记τa是a的首中时

第一个自然的问题是τa是有限的吗?第二个问题是如果有限,其期望是多少?或者什么分布?鞅方法可以回答这些问题,为了回答这些问题,最重要的是找到合适的鞅.取z＞0,那么zXn是独立随机变量的乘积,且(www.daowen.com)

其中(Fn)不妨被看成为X的自然流.因此

是一个鞅.这个鞅称为指数鞅,是个非常有用的鞅.我们用它来计算P(τ＜∞)以及τa的母函数E[zτa].为什么计算母函数?因为按照期望的定义

n

母函数的Taylor展开式的系数就是τa的分布律.当然上式的收敛半径至少是1.

由Doob的定理,应该有

一个显然的事实是,当τa＜∞时,有Xτa=a,也就是说X在它首次到达a的时候肯定恰好在a处.因此我们有

随后只需让(zp+z-1q)-1=x反解出z就得到τa的母函数.但是这里有几个需要解决的问题,首先Doob的定理只适用于有界停时,没有任何理由说τa是有界停时,所以我们不能直接用Doob的定理.但我们可以对τa∧n用Doob定理,因为它是有界停时.因此代替(2.1.5)式有下式成立

现在让n趋于无穷,那么τa∧n趋于τa,但问题是极限和期望是否能够交换?当z＞1时,因为τa∧n≤τa,由τa的定义知Xτa∧n≤a.另外如果再有zp+z-1q＞1,那么

应用有界收敛定理,极限和期望可以交换,因此

怎么才能同时满足z＞1和zp+z-1q＞1两个条件呢?当p≥q时,这意味着z＞1;而当p＜q时,意味着z＞q/p.在前一种情况下,让z↓1,得P(τa＜∞)=1;在后一种情况,让z↓q/p,得

也就是说,当概率偏向右的时候,随机游动会在有限时间内到达右边的点,但在有限时间内到达左边点的概率小于1.在前一种情况,我们算出τa的母函数为

这时

当p=q=1/2时,E[τa]=+∞.

现在设b＜0＜a,τa,τb分别是随机游动首次到达a与b的时间.令τ=τa∧τb是随机游动首次到达其中一点的时间,那么由上面得到的结论,只要0＜p＜1,就有也就是说随机游动必定会在有限时间内离开这个区间.现在我们想知道到底随机游动从b点(或者从a点)离开的概率有多大?这是经典的赌徒输光问题.

当p＞q时,X就不是鞅了,这时我们又需要一个指数鞅.因E(q/p)ξn=p+q=1,故不难验证{(q/p)Xn}是鞅.同理有

答案也可以用全概率公式列出差分方程解出.

练习2.1.4　找适当的鞅计算上面例子中τ的母函数.

下面我们将证明Doob的两个基本不等式,极大不等式和上窜不等式.它们其实是Doob基本定理的应用.

引理2.1.1　设X是一个下鞅,那么对任何λ＞0及正整数N,有

证明.令τ:=min{0≤n≤N:Xn≥λ},则τ是一个停时且τ≤N,故

把右边第二项移到最左边,就推出我们想要的不等式.

定理2.1.4　(Doob)设X是一个非负下鞅.

(1)对任何λ＞0及正整数N,

(2)对任何p＞1及正整数N,

证明.(1)是引理2.1.1　的直接推论.

再结合Fubini定理和H¨older不等式

这个不等式推广了在独立随机序列场合著名的Kolmogorov不等式.再因为{|Xn|}是非负下鞅,用于第二个不等式p=2的情况,得

这个不等式可以推出上面的不等式(差个常数).

下面我们讨论上窜不等式.设X是实值适应随机序列,对-∞＜a＜b＜∞,

定义

(约定inf∅=+∞)则{τn:n≥1}是一个严格单调上升的停时序列,对N≥1,

令

随机变量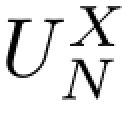[a,b]记录了随机序列X在时刻0与N之间从a下跳至b上的上窜次数.下面是著名的Doob上窜不等式.

定理2.1.5　(Doob)设X是一个下鞅,则对任何正整数N,常数a＜b,

注意τn关于n是严格递增的,故上面的和实际上都是有限和,它分成为上窜的和与下窜的和两个部分,两个和的处理方法完全不同,上窜的和是利用样本轨道性质,而下窜的和是利用下鞅均值的递增性质.

现在,由定理2.1.3　推出右边括号中的每一项的期望都是非负的,因此

得到所要求的结论.

这个证明在逻辑上已经完成,但若仔细想一想的话,不等式的证明思想是非常漂亮的.为什么这么说呢细心的读者可能已经注意到证明中实际上有一个直观上的矛盾.既然上窜的部分和是正的,那么下窜部分和似乎是负的.为什么从轨道来看是负的下窜部分和在期望之后会变成正的?也就是说直观地看,Yτ2n+1∧N似乎是小于Yτ2n∧N,但为什么期望会反过来?想清楚这个问题对初学者有很大的帮助.

证明.设X*,X*分别是{Xn}的上极限与下极限.显然

由上窜不等式

定理2.1.6　中下鞅的收敛形象地说是向右收敛,在本节的最后,我们将证明下鞅向左的收敛定理,下面定理说明这样的收敛要容易得多.

定理2.1.7　设X=(Xn)n≤0是关于流(Fn)n≤0的下鞅且infn EXn＞-∞,则

(1)X是一致可积的;

(2)当n→-∞时,Xn几乎处处且L1收敛于一个可积随机变量X-∞,且对任何n,

证明.设n≤0,因EXn≥EXn-1,故infn EXn＞-∞蕴含着limn→-∞EXn存在且有限,记为x.对给定ε＞0,取k使得EXk-x＜ε,那么当n≤k时,

由此推出X是一致可积的.

(2)收敛部分类似于定理2.1.6　的证明.对于后一部分,对A∈F-∞及m＜n≤0,有E(Xn;A)≥E(Xm;A),让m→-∞,

因此E(Xn|F-∞)≥X-∞.