对于Rn上任意的有限测度μ,定义

其中(x,y)是Rn上的内积,被称为μ的Fourier变换,在概率论中一般称为特征函数,虽然名称不同,本质上是一样的.特别地,如果μ是n-维随机变量ξ的分布,那么

也称为是ξ的特征函数,当然特征函数仅依赖于分布.

特征函数是Rn上一个有界连续的复值函数,它在零点的光滑程度基本上可以刻画μ在无穷远处测度的大小.

Fourier变换是分析中最重要的方法之一,在概率论与随机分析的研究中也有必不可少的重要性.

特征函数第一个重要性质是可以将卷积化为乘积.设μ,ν是两个有限测度,那么定义它们的卷积

卷积是一个重要的概念,它在概率论中就是分布分别为μ,ν的独立随机变量ξ,η的和的分布.

定理1.3.1

特征函数第二个重要性质是其唯一性,也就是说特征函数作为有限测度到连续函数的变换是一一的.

定理1.3.2　设μ和ν是Rn上两个有限测度,如果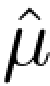(x)=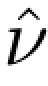(x)对所有x∈Rn

成立,那么μ=ν.实际上,下面的命题等价

(1)μ=ν;

(2)对任何有界可测函数f,μ(f)=ν(f);(www.daowen.com)

(3)对任何有界连续函数f,μ(f)=ν(f);

(4).

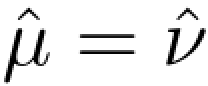(1)蕴含(2)是单调类定理,(4)蕴含(1)是唯一性定理,其他是平凡的.这个性质是分析中极其重要的工具,也就是说,为了证明两个测度相等,我们只需要证明两个测度的特征函数相等,在很多情况下这会容易许多.另外当我们无法确定一个随机变量的分布时,也许可以确定它的特征函数,特征函数将唯一地识别出分布.

练习1.3.2　设ξ,η是随机变量,后者可积.如果对任何x∈Rn有

证明:E[η|ξ]=0.

特征函数最后一个重要性质是连续性,尽管它在本讲义中并没有真正被使用.说一个有限测度列μn弱收敛于μ,如果对任何有界连续函数f有

定理1.3.3　(L´evy)μn弱收敛于μ当且仅当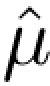n点点收敛于.

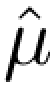这个定理是证明著名的中心极限定理的利器,一直到多年前,它几乎就是唯一的方法.

它是整数加群上的一个函数.类似于特征函数的还有母函数与Laplace变换,它们本质上是一样的,适用的范围不同,特征函数可以适用于所有随机变量,母函数适用于数列,一个数列{an:n≥0}的母函数定义为一个幂级数

当幂级数的数列半径为正时,它一样可以唯一确定它的系数.Laplace变换适用于在支撑在正半轴[0,∞)上的测度,这样一个有限测度μ的Laplace变换定义为

类似地,Laplace变换一样可以唯一确定测度μ.