严格地说，跳转优化(jump optimization)并不是特指某一个优化算法，而是一类优化算法的总称，它们能够完成大多数分支、跳转相关的优化工作，有时，亦称为“分支优化”。与先前讨论的优化算法不同，跳转优化是比较典型的控制流优化算法。因此，它基本上都是基于流图进行的，很少依赖于数据流分析的支持。在实践中，虽然跳转优化经常被应用于IR优化及目标代码优化中，但并不太适用于HIR。现代编译技术的观点认为跳转优化的最佳时刻是在代码最终形态基本确定之后。

实际上，跳转优化的思想并不复杂，已经成为了编程的规范，只是读者并没有察觉而己。下面，来谈两个最常见的跳转优化方案。

1．条件跳转优化

有一个事实是不得不承认的，那就是条件跳转的复杂程度要远远大于无条件跳转。实际上，条件跳转优化的思想是非常简单的，就是将永真或永假的条件跳转替代为无条件跳转，或者将其删除。首先，读者可能会有一个疑问，即永真或永假的条件跳转是否存在？回答是肯定的。在IR生成过程中，编译器设计者会避免永真或永假的条件跳转，保证原始生成的IR不存在此类跳转。但是，常量传播、常量折叠以及代数简化等算法为我们做了很多工作，因此，现阶段的IR与原始生成的IR相比，早已是面目全非了。

一般来说，针对永真或永假的条件跳转，主要采用如表7-9所示的优化方式。从表面上来看，这种跳转优化的意义可能难以理解，尤其是将JT、JNT转换为JMP，似乎并没有节省任何IR。不过，这种优化对于检测不可到达代码的作用是非常显著的。举个简单的例子，读者应该不难想象，假设把JT转换为JMP，那么，就意味着JT跳转的假分支代码极有可能变成不可到达代码。同样，JNT的情况也是类似的。下面，来看一个条件跳转优化的实例。

表7-9 条件跳转的优化方式

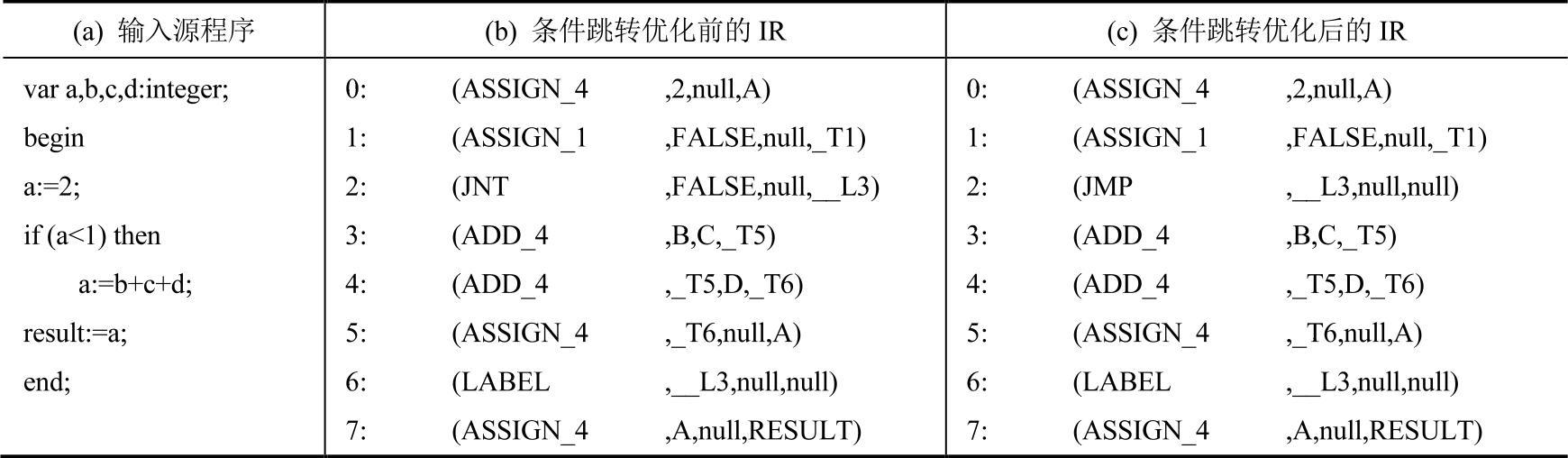
例7-7 条件跳转优化的实例。见表7-10。

正如先前所述，基于原始IR直接讨论条件跳转优化的意义并不大。通常，条件跳转优化的基本环境是由其他IR优化算法创造的，而不是来自原始IR。因此，笔者并没有给出原始的IR形式。在本例中，不难发现，(c)列中的第3、4、5行IR都是不可到达代码，也就是在任何情况下都无法执行的代码。在稍后的不可到达代码删除优化中，就可以将这部分代码删除。

表7-10 条件跳转优化的实例方式

2．连续跳转优化

从一条跳转指令转移到另一条跳转指令的情况是极其常见的，尤其是当采用简单的代码生成策略时。例如：(www.daowen.com)

不难发现，由于JNT指令的跳转目标Ll处的指令是另一条无条件跳转，因此，完全可以将JNT指令的目标直接设为JMP指令的目标，以减少目标程序中冗余的跳转指令。这种替换并不依赖于JNT指令中的条件值。与条件跳转优化不同，连续跳转优化并不会创造新的不可到达代码情形，它仅仅是通过优化跳转的形式，以提高目标程序的执行效率。

连续跳转优化既可以适用于IR，也可以适用于目标代码。这里，只讨论IR优化中的连续跳转优化问题。在IR列表中，试图检测代码中的连续跳转情形并不复杂，只需要简单地查看每一条跳转的目标是不是另一条跳转指令即可。一般来说，可以将连续跳转的情形分为如表7-11所示的几种。

表7-11 连续跳转优化的方案^[1]

前三种连续跳转情形的优化方案是不需要作任何论证的，它也不依赖于JNT指令的条件值，因此，相关实现也是非常简单的。下面，来分析最后一种情形。

最后一种情形比较复杂，并不是在任何情况下都可以优化的。仅当两个条件都为真时，才可能优化。看似这个要求并不苛刻，不过，稍加思考后，不难发现，在编译阶段，试图确定两个条件是否同时为真并不是一件容易的事情。当然，这里并不考虑两个条件为布尔常量的情况，假设编译器是无法计算出这两个条件的实际取值的。那么，在很多情况下，编译器将无法作出两个条件是否同为真的判定。注意，这个问题的关键就在于“很多情况”，而不是绝对不可能。有读者可能会有疑惑，既然两个条件的实际取值都不知道，那么，如何判定它们是否同为真呢？事实上，在特定的情况下，这是可能的。例如：

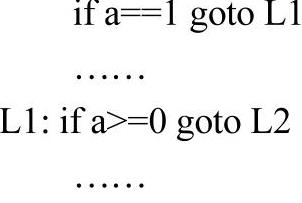
编译器并不能预知a==l、a>=0的实际取值，但可以得到一个结论，即当a==l为真，则a>=0必定为真。因此，可以将第1行代码优化为“if a==l goto L2”。当然，在更多情况下，这个问题是不可判定的。例如：

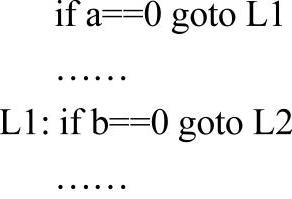
编译器试图确定a==0与b==0的取值关系是不可能的。理论上说，在特殊条件下，这种优化方式是可行的。但从实现的角度来说，在无法计算实际取值的情况下，设计一个判断两个条件是否同时为真的算法是非常困难的。而且其优化的效果也十分有限。因此，即使是VC++之类的商用编译器也没有做相关分析与优化。