代数简化(algebraic simplification)也称“代数化简”，其基本思想就是利用运算符或运算符及操作数的特殊组合的代数性质来简化表达式的形式。初次接触这个定义的读者可能会联想起深奥的数学，难道代数简化背后蕴含着复杂的数学理论吗？事实恰恰相反。虽然笔者尚不敢确定代数简化是不是最简单的优化算法，但至少也是最简单的优化算法之一。

先来看一些简单等式：

i+O=i、i-O=i、i*l=i、i/l=i、b or true=true、b and false=false、b shr O=b

．．．．．

从数学上来说，这些式子都是成立的。而代数简化就是利用这些简单等式的性质，达到简化代码的效果。例如，可以将y←-x or true转换为y←true。同样，也可以将p←q+0转换为p←q。当然，在数学中，类似的等式是常见的，因此，其规模可能非常庞大，试图逐一枚举恐怕并非易事。这里，笔者并不打算列举各种代数简化等式，当然，这样做的本身意义也并不大。代数简化的意义就是简化表达式的运算，这应该不难理解。

有些代数简化也可以看成是强度削弱，即用一种计算速度较快的运算来替代另一种相对较慢的运算。例如，可以将i^*8转换为i shl 3。这种转换的主要原因就是移位运算的速度要远远超过乘、除运算。在一些RISC结构的目标机中，强度削弱的应用是非常广泛的。由于目标机指令系统可能不支持某些复杂的运算指令，此时，强度削弱的替换思想就是不错的应对之策。最常见的是用一串移位和加、减运算来替代乘、除运算。例如，t<-i*5可以用

t←-i shl 2、t←t+i

代替。而t←-i^*7可以用

t←-i shl 3、t←t -i

来代替。当然，强度削弱并不局限于优化阶段。实践证明，有些强度削弱的思想应用在代码生成阶段的效果可能会更佳。下面，来看一个代数简化的实例。(www.daowen.com)

例7-6 代数简化的实例。见表7-8。

代数简化通常只针对一条IR进行操作，并不会影响上下文。这是代数简化的一个重要特点。在这个实例中，代数简化算法主要作用于三条IR上，即第2、5、9行IR。下面对每一次化简稍作解释。

表7-8 代数简化的实例分析

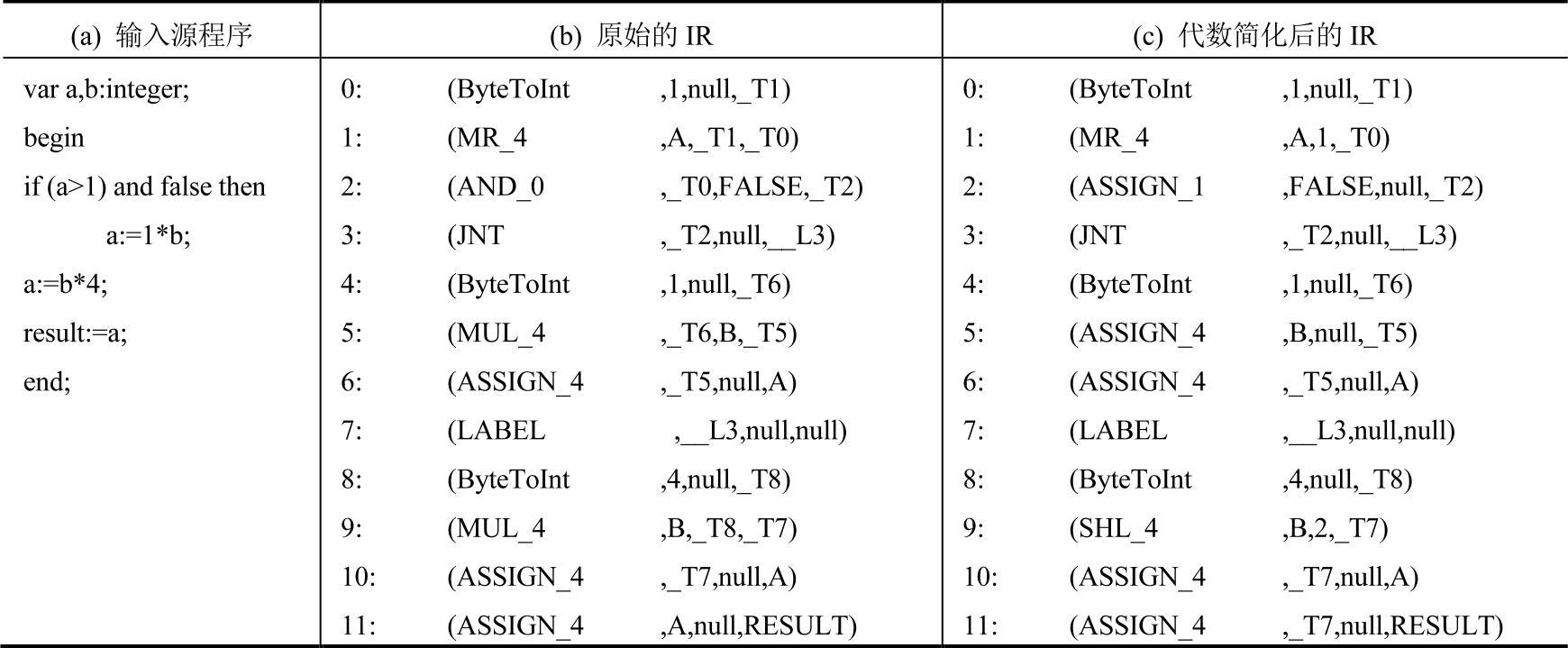
第2行的化简依据就是等式i and false=false，这显然是成立的。

第5行的化简依据就是等式i* l=i。当然，这是基于常量传播后才能化简的。

第9行的化简依据就是等式i* 4=i shl 2。同样，这也是基于常量传播后才能化简的。

仅从这个实例分析，似乎并没有看到代数简化的明显优势。除了强度削弱之外，更重要的是，这一遍代数简化为常量传播创造了新的机会。例如，将第2、5行都替换成了赋值形式，这种形式最有利于进行常量传播。在实践中，这种渐进式的改善是非常有效的，许多看似棘手的问题可能在无意间就被化解了。在本例中，最终可以借助于这种渐进式优化的思想将整个if语句删除，这个效果应该是令人满意的。

代数简化一般都是针对某一条IR进行的，所以不必过多考虑基本块或其他流图的因素。当然，代数简化也不太关注IR的级别，一般而言，HIR或LIR都是可以接受的。不过，笔者还是推荐使用HIR或MIR实现代数简化，那样可能会得到更好的优化效果。