全局数据流分析的关键就在于根据流图及基本块内的数据流值来分析得到整个流图各点的数据流值。那么，全局数据流问题的求解过程必定是读者关心的。

根据数据流的实际问题，通常是以数据流方程作为求解与算法实现的依据。事实上，很多数据流问题都可以以方程的形式加以描述。根据实际编译器设计的经验，计算机科学家提出了许多经典的数据流模式，例如，活跃变量分析、到达一定值分析等。其中，活跃变量分析是一个经典实例，它具有深远的现实意义。本小节将重点讨论活跃变量的相关话题。

假设一个基本块s，其入口处的活跃变量集合为in[s]，而其出口处的活跃变量集合为out[s]。那么，必定有下式成立：

out[s]=Uin[i] （其中i是s的后继基本块） 【式7-1】

这个等式的含义就是基本块s出口处的活跃变量必定是其后继基本块入口处活跃变量集合的并集。同样，可以将等式描述为某一基本块入口处活跃变量的集合等于其前驱基本块出口处活跃变量集合的并集。

令use[s]为基本块s中所引用的变量集合。注意，这里讨论的“引用”指的是在某一基本块内，某些点引用的变量的定值来自当前基本块外。在数据流问题中，仅关心这类特定的引用，而不需要关心那些来自当前基本块的引用点变量的定值。

同样，令def[s]为基本块s中所定值的变量集合。那么，不难得到下式：

in[s]=(out[s)-def(s])Uuse[s] 【式7-2】

这个等式的讨论对象就是基本块入、出口处的活跃变量与块内引用、定值的关系。式7-2的观点是基本块入口处的活跃变量集合由以下两部分组成：

(1)基本块内所引用的变量集合。

(2)基本块出口处的活跃的且在块内没有定值的变量集合。

值得注意的是，千万不要误认为in[s]=use[s]，这样就忽视了s的后继基本块对in[s]的影响。有了这两个等式之后，就明确了活跃变量集合在基本块内及块间的变化关系，那么，求解活跃变量问题就变得比较容易了。下面，通过一个实例来分析活跃变量的求解过程。

例7-1 参考图7-4，求解该流图的活跃变量集合。

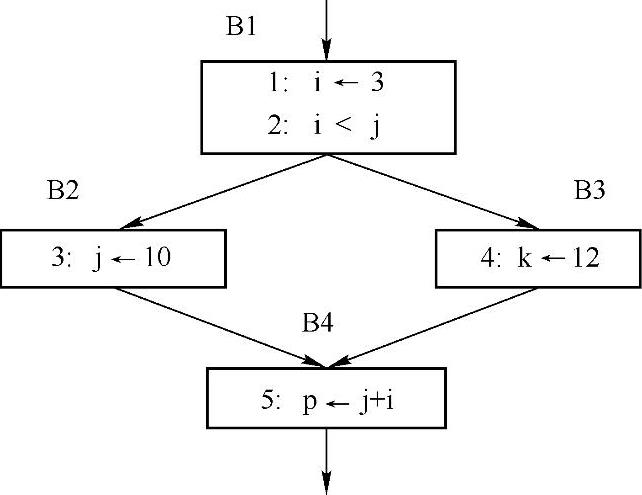
图7-4 求解活跃分析示例流图(www.daowen.com)

(1)求解use、def集合。

求解use、def集合完全依赖于IR的实际语义，本例中并未涉及指针引用等复杂语义。求解的结果如表7-2所示。注意：use[Bl]中没有i的原因是i在引用前己在本基本块内被定值，所以i不需要加入use[Bl]集合。

表7-2 与图7-4对应的use、def集合

(2)求解in、out集合。

不难发现，从最后一个基本块开始向前计算可能更容易。假设变量p在B4后继块中是不活跃的，即out[B4]={}。那么，可以分别得到如下集合：

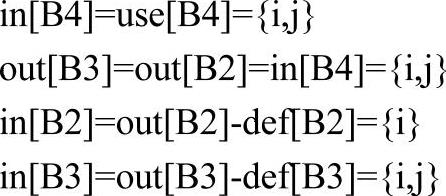
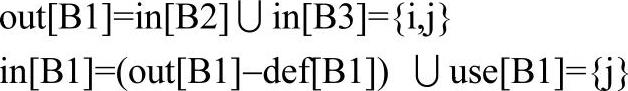
根据上述计算，可以得到如表7-3所示的结果。

表7-3 与图7-4对应的in、out集合

从本例中，不难发现，根据数据流方程，计算活跃变量集合并不复杂。由于图7-4是一个无环图，因此，一次迭代即可顺利完成分析过程。如果流图存在环时，迭代过程会复杂一些，可能需要数次迭代才能完成。不过，不必担心迭代无法终止的情形，事实上，计算机科学家已经用数学方法证明了数据流方程是有解的。

最后，读者的疑问可能就是：计算活跃变量集合的意义是什么？在此，笔者稍作简单说明。非活跃变量即死变量，也就是说该变量在该集合所处位置点后不会有任何引用。从优化的角度而言，可以删除基本块内所有对块出口处已死变量的定值操作，因为这类定值是没有任何实际意义的。例如，在图7-4中，发现B4中对p的定值以及B3中对k的定值都是无意义的。如果将这两条语句删除后再求解一次活跃变量集合，则会发现出现了新的死变量，这就是优化算法通常需要多次迭代的原因所在。事实上，根据图7-4所示的流图，最终优化算法可以删除所有的语句。