现代程序设计语言的类型系统通常包括如下四个部分：基本类型、新类型构造规则、类型等价或相容规则、类型推断规则。很多语言还提供了一些类型隐式转换的规则。下面，从编译器设计角度来详细描述各部分的作用。

1．基本类型

绝大多数语言的基本类型都是从三个原子类型（即数值、字符、布尔值）引申得到的，其中数值是最为复杂的，它可以细化成各种基本类型。例如，数值可以分为整数类型、实数类型。而根据不同的程序设计语言，又将整数类型定义为integer、byte、word、longword等整数类型。而实数类型又可以细化为float、double等。一般来说，现代大多数程序设计语言都提供了非常丰富的基本类型，以便程序员有更多的选择。

程序设计语言通常从两个方面细化整数类型，即长度、符号位。符号位相对比较简单，而长度就复杂些了。有些语言使用绝对长度描述基本类型，即在语言的类型系统中明确规定各种基本类型占用的bit或byte的数量，如Fortran、Ada等。而有些则是以相对长度描述基本类型，即只描述各种基本类型之间的相对关系，具体的实现是由编译器设计者规定的。例如，C语言规定long long类型的长度是long类型的2倍，但并没有严格定义long或者long long的实际长度。

当然，针对实数类型而言，实数的表示形式也是一个可细化的方面。例如，实数的尾数的精确位数、阶码的表示范围等。大多数语言的实数类型的表示形式都是遵守IEEE 754标准的，所以其表示形式还是比较一致的。

以上从语言及编译器设计的角度对基本类型作了简单介绍。由于基本类型比较简单，笔者就不再耗费篇幅了。

2．新类型构造规则

程序设计语言的基本类型通常是硬件支持的数据存储方式的一种抽象，但是这却不足以满足程序员处理复杂数据结构的需要，例如，图、树、表、栈、数组、串等。这些数据结构与基本类型的主要区别在于它们通常需要一组对象加以描述，如何将基本类型组合或复合为这些复杂的数据结构是高级语言设计者必须思考的问题。

在程序设计语言中，有些复杂类型需要语言本身的支持，如数组、串、枚举、结构、指针等。而复杂类型可以由前者合成，如树、图等。语言设计者通常将前者作为类型系统的一部分，明确说明其构造原则。下面，笔者针对语言设计中最常见的数组作简单分析，以便读者了解如何在类型系统中构建复杂类型。

通常，在类型系统中，数组类型需明确说明如下几点：

(1)数组的基类型。有些语言规定数组的基类型只能是语言支持的基本类型，而更多的语言则允许基类型是任意类型，甚至是数组。

(2)行（列）优先原则。例如，Fortran是列优先，而C、Pascal都是行优先。

(3)数组操作的支持。有些语言支持对整个或部分数组赋值，例如，当a，b，c是大小、形状相同且基类型支持加法运算的数组时，Fortran 90允许使用a=b+c将b，c各单元元素相加后送到a的相应单元中。而C、Pascal对于数组的操作则相对比较简单。

(4)最大维度。数组的最大维度理论上是没有限制的。大多数语言设计者也认同这一观点。

(5)物理存储形式。即如何分配数组的物理存储空间，以及以什么形式存储数组元素。

(6)数组声明的语法、语义形式。

不难发现，上述说明并不复杂，都是一些最基本的元素。对了解程序设计的读者来说，应该是非常简单的。因此，不必花较大篇幅评说各种复杂类型。注意，类型系统是程序设计语言的一部分，类型系统的描述可以是形式化的，也可以是非形式化的。从编译器设计的角度来说，不必拘泥于小节，只要能明确、清晰说明语言的类型即可。

3．类型等价或相容规则

实际上，类型等价和类型相容是不同的概念，所谓“类型等价”就是指对于程序设计语言而言，两个类型是相同的。而所谓“类型相容”就是指对于程序设计语言而言，两个类型是兼容的，即可以通过一定的隐式转换使两个类型等价。类型等价是类型相容的充分条件。类型相容的规则更多应用于确定特定类型的对象是否满足特定上下文的需要。下面，先来谈谈类型等价的话题。

程序设计语言判断两个类型是否等价的标准是什么呢？不妨先分析图6-1的实例。

图6-1 类型等价实例

在图6-1中，Node类型与TableNode类型是否等价呢？这就引出了两个等价标准，即名字等价和结构等价。

名字等价的观点是：两个类型等价的基本条件是类型名字必须相同。根据这一条件，图6-1的类型是不等价的。严格意义上的名字等价是不可取的，因为当项目规模较大时，名字的一致性是很难维护的。通常，实际编译器很少采用严格的名字等价。不过，有些语言支持类型命名机制，那么，由此可能产生类型别名。如果将类型别名考虑在内，名字等价还是具有实际意义的，这种机制有时称为“宽松的名字等价”。例如，在C语言中声明typedef struct p q；（其中p是一个己声明的结构类型），即表示q是类型p的别名。在这种情况下，按严格的名字等价机制来说，q与p显然不是等价类型。不过，由于q只是p的一个别名，按宽松的名字等价机制来说，q与p是等价类型。注意，实际编译器中所讨论的名字等价都是宽松的名字等价。名字等价的优点在于实现比较简单。

结构等价的观点是：两个类型等价的基本条件是它们的结构必须相同。根据这个条件，图6-1的类型是等价的。结构等价的判断标准要比名字等价宽松得多，也更灵活。不过，很少有程序设计语言选择结构等价作为判断标准。结构等价表面上看似乎比名字等价更合理，实则不然。主要有如下三个原因：

(1)无法区别设计本意不同但结构完全相同的两个类型。如图6-2所示。

图6-2 结构等价实例

不难发现，根据结构等价的观点，图6-2所示的两个类型是等价的。不过，这个判断结果似乎明显违背了程序员的本意。这种歧义的等价结果不但没有太大的意义，甚至还有可能引发一些问题。

(2)结构等价的实现也比较复杂，而且根据源语言的特点，可能还需要考虑递归类型声明的情况。尤其当基本类型比较丰富时，判断算法的效率可能比较低。(www.daowen.com)

(3)由于不同程序设计语言的特点不尽相同，结构等价的定义也就各有不同了。例如，有些语言并不强调结构类型中域的顺序，这样判断算法就会非常复杂。

下面，举两个实际语言的例子来说明类型等价问题。

C语言明确指出其使用宽松的名字等价规则，结构、联合以及typedef皆是如此，而C语言的基本类型都是互不等价的。只不过由于C语言是弱类型语言，有较丰富的类型相容规则，读者千万不要认为C语言类型就是互相等价的。

Pascal的类型等价问题就比较模糊了，Pascal报告中并没有明确提到“类型等价”的概念。一般来说，Pascal语言的类型等价问题更多依赖于具体编译器的实现。这里，笔者以Turbo Pascal为例，说明Pascal的类型等价问题。

例6-1 Turbo Pascal的类型等价。

在本例中，a，b，c，d，e中有几组类型等价的变量呢？答案只有一组，即(a，b，f)。为什么昵？从理论上分析，可能并不容易理解其中的原因。实际上，从符号表设计的角度就非常容易得到这个答案。根据前面所介绍的符号表结构，可以得到如图6-3所示的符号表结构。

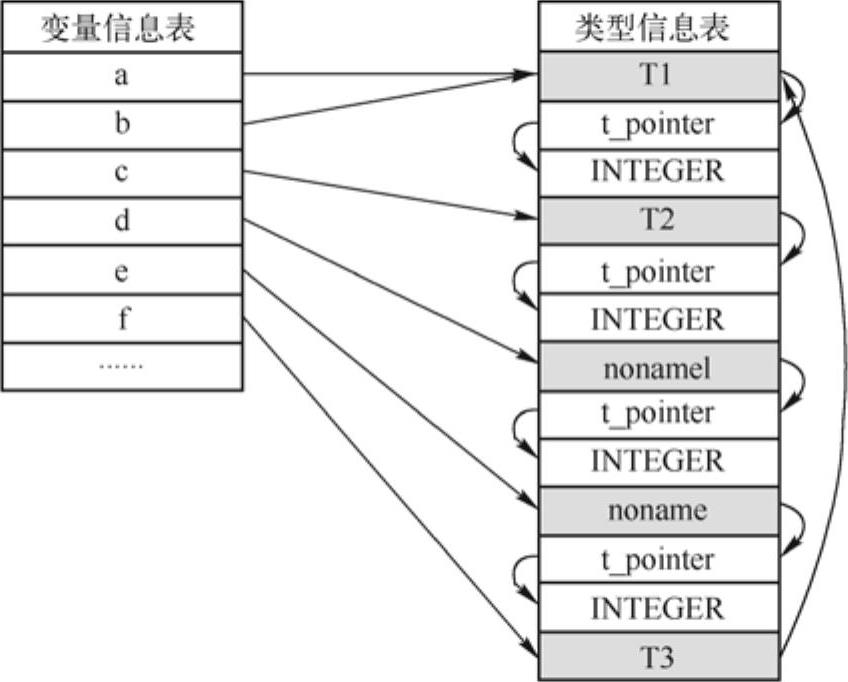
图6-3 符号表示意图

从符号表中，不难得到一个结论：Turbo Pascal判定类型等价的标准是从变量的类型指针开始，跃过所有类型别名结点（例如，本例中的Tl、T2、T3、nonamel、noname2）后，如果指针指向同一个类型结点时，则认为两个变量的类型是等价的，否则认为它们是不等价的。例如，判断f与a变量的类型等价的过程如下：分别跃过别名结点T3、Tl，最终都指向了第二行的t_pointer结点，由此推断它们是等价的。这种观点得到许多Pascal编译器设计者的认同。Neo Pascal的类型等价规则与Turbo Pascal是一致的。

讨论完类型等价问题，再来看看类型相容的话题。

前面已经简单介绍了类型相容的概念。从实践的角度来说，类型相容更多关注的是类型之间的隐式转换是否可行。例如，在Pascal中，讨论INTEGER与REAL类型是否相容的问题，就是明确将哪个类型作为标准类型。如果将REAL作为标准类型，那么，将INTEGER类型隐式转换为REAL是完全可行的，在这种情况下两者是相容的。但是，如果将INTEGER作为标准类型，而将REAL类型隐式转换为INTEGER则是不可行的，这种情况下两者就不相容了，而只能借助于显式转换。

通常，程序设计语言讨论类型相容是基于一个特定的上下文环境讨论的。只有在一定的上下文环境下，才有标准类型（或者称为上下文期望的类型）的概念。一般而言，需要在以下几种上下文环境下考虑类型相容：

赋值语句：右部表达式类型必须与左部表达式的类型相容。此时，左部表达式的类型作为标准类型。

运算表达式：根据不同的运算表达式的需求，操作数的类型必须与运算表达式期望的类型相容。

函数传参：实参的类型必须与形参类型相容，此时，形参类型作为标准类型。

函数返回值：实际返回值表达式的类型必须与函数声明的返回值类型相容，此时，声明类型作为标准类型。

关于类型相容性的定义，不同的程序设计语言有各自的理解。有些语言比较严格，而有些语言就比较宽松。C语言就是一种非常宽松的语言实例，在C语言中，所有的数值类型都是相容的。即使用double变量给char变量赋值，依然是合法的，其中的隐式转换完全由编译器完成。然而，Pascal语言就严格一些。关于类型相容的宽严之争，学界并没有统一的观点。

4．类型推断规则

在C语言中，己知a、b的类型是unsigned char，是否可以判断a+b的类型呢？读者可能会不假思索地认为结果类型也是unsigned char。这个答案正确吗？假设a、b的值都是255的情况下，a+b的值为510，显然已经远远超过了unsigned char类型的表示范围。有读者可能会觉得运算结果溢出应该由程序员控制，而不应当由编译器处理。这种说法并非没有道理。确实，在实际编程过程中，有一些数据溢出的错误是应该由程序员自行解决的。如果程序员将a+b的结果赋给了一个char类型的变量，因此所产生的溢出完全应由程序员负责。但是，如果程序员将a+b的结果赋给了一个int类型的变量，计算结果却由于a+b运算结果的溢出而不正确，难道这也要程序员买单吗？显然，这是令人无法接受的。那么，如何才避免此类溢出的发生？通常，需要编译器根据每一个表达式的操作数类型，推断获得其运算结果的类型，这种推断机制就是类型推断。

那么，类型推断又是如何达到预期目标的呢？实际上，在设计程序设计语言时，设计者根据类型系统及运算符的实际状况，推导出类型与运算符各种组合之下的结果类型。然后，将这些推导结果整理形成一种映射关系，这就是类型推断规则。编译器就是根据这些规则机械地完成类型推断工作的。

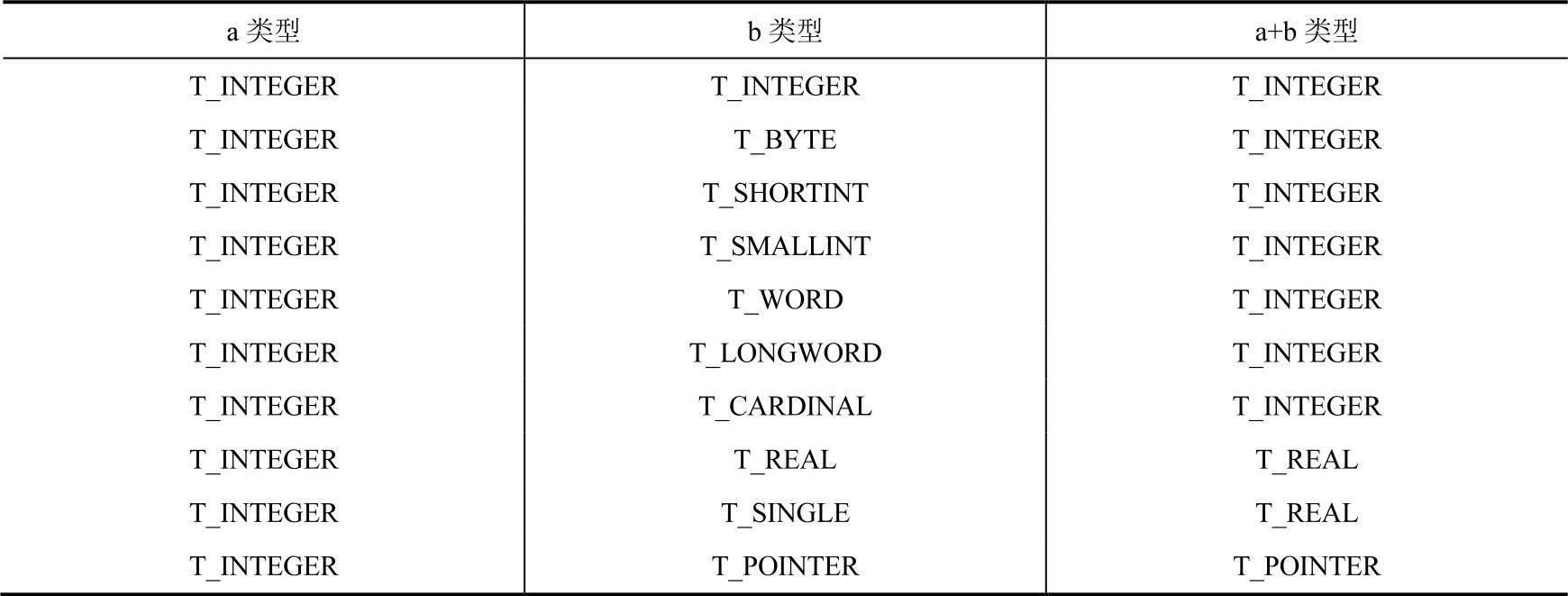
下面，先看一个简单的类型推断规则的实例。这是部分Neo Pascal类型推断规则。从表6-1分析，不难想象，完整的类型推断规则的规模应该是非常庞大的。一般而言，可以得到如下结论：

R≥Op×T×T

其中，R表示类型推断的规则数量，Op表示双目运算符的种类数，T表示语言预定义类型种类数。Neo Pascal的规则数量大约为1300条左右。然而，有些语言引入了类型提升的概念，从编译器设计的角度而言，它可以将类型推断描述为一个规则函数的形式。

表6-1 类型推断规则

以上只讨论了类型推断的一个话题，即表达式类型推断。当然，这是类型推断的主要工作。实际上，除此之外，类型推断的工作还包括推断常量的类型。在编程过程中，程序员不可避免地会使用常量。但是，常量到底是什么类型的呢？程序设计语言无法要求程序员像声明变量一样，说明常量的类型。有读者可能会反驳，在C语言中，声明常量通常也需要指出类型的。实际上，这种形式的常量是符号常量，的确有些语言要求程序员为符号常量指明类型，但这并不是普遍的，Pascal语言的符号常量是不需要类型信息的。然而，读者可能忽略了一种更常用的常量，例如，cos(3.4)，其中，3.4就是一个常量。针对这种情况，相信没有一种语言要求程序员指明其类型信息的。当然，3.4也不能没有类型信息，而它的类型必须由编译器推断得到。较之表达式的推断，常量类型的推断要简单得多，只需根据常量的取值选择合适的类型即可。当然，常量类型推断也有一定技巧，例如，对于正整数而言，将其推断为无符号类型还是有符号类型是存在一定区别的。不同程序设计语言及编译器对于这些细节的定义与实现是不尽相同的。在常量推断方面，有些语言的处理非常简单，即尽可能选择高级类型描述常量，而并不要求精确推断。

最后，笔者还必须指出一点，对于C、Pascal之类的结构化语言，类型推断机制是很简单的。有些语言特性却可能会使类型推断变得极其复杂，例如，BASIC语言不强制要求变量声明，编译器只能够从上下文中收集线索并作出推断。再如，面向对象语言的派生类、多态性、重载、泛型、作用域规则等特性同样会使得类型推断变得复杂，C++的类型推断机制正是如此。而函数式语言ML在类型推断方面是研究最深刻且做得最好的语言之一。