本小节将详细分析Neo Pascal语法分析表的构造过程及结构设计，同时，还将着手解决实际语法分析表构造过程中的一些常见问题。

前面，笔者介绍的LL(1)语法分析器只是一个抽象模型，或者说只是一个伪代码描述的算法而已，与实际的语法分析器还存在一定差异。其中，最主要的问题就是语法分析表的构造及结构设计。

1．构造语法分析表

仅从文法的篇幅而论，Neo Pascal的文法的确比先前所分析的任何例子都要长得多。显然，这会给构造其语法分析表带来一些麻烦，不过，其核心方法却是不变的。首先，准确计算得到文法的First集合及Follow集合。然后，根据First集合及Follow集合构造语法分析表。其中，在构造语法分析器时，计算文法的First集合及Follow集合是最烦琐的。不仅需要熟练掌握其计算方法，还需要有相当耐心才能完成。当然，读者也可以应用一些自动生成工具构造语法分析表或者语法分析器。有关自动生成工具的使用并不是本书讨论的重点，读者可以参考相关教材。

下面，笔者给出Neo Pascal文法的First集合及Follow集合，供读者参考。

First集合见表3-4。

表3-4 Neo Pascal文法的First集合

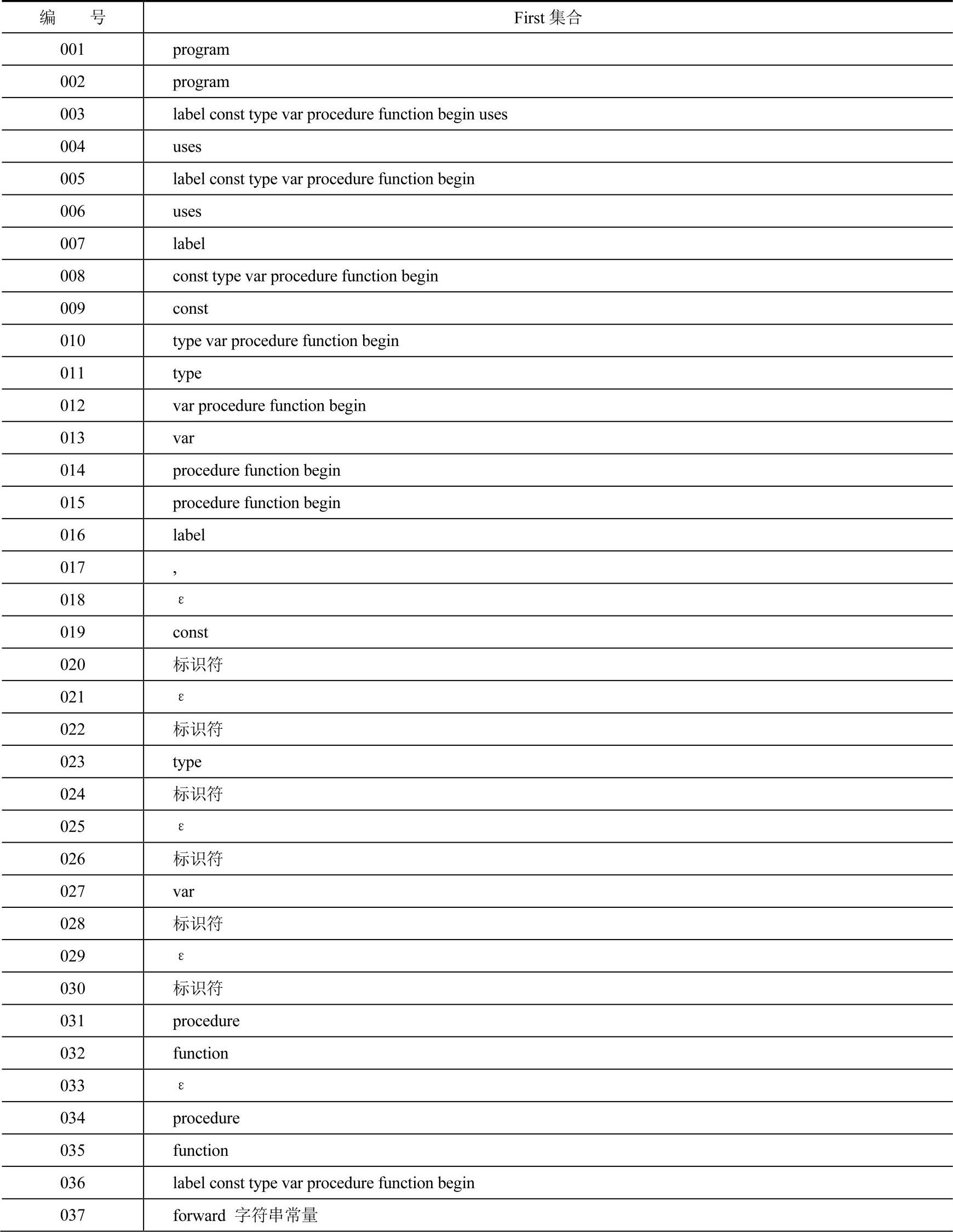
（续）

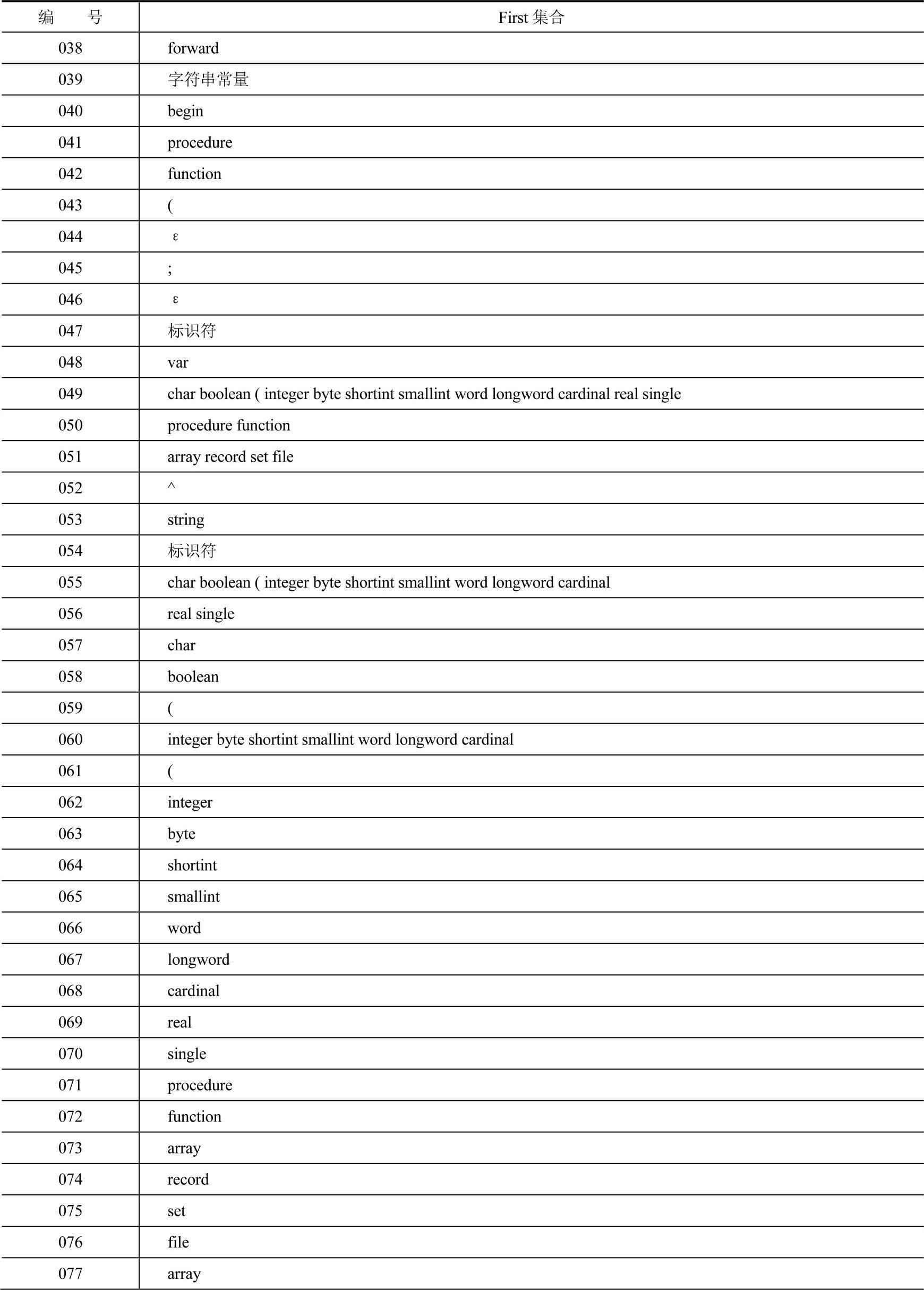
（续）

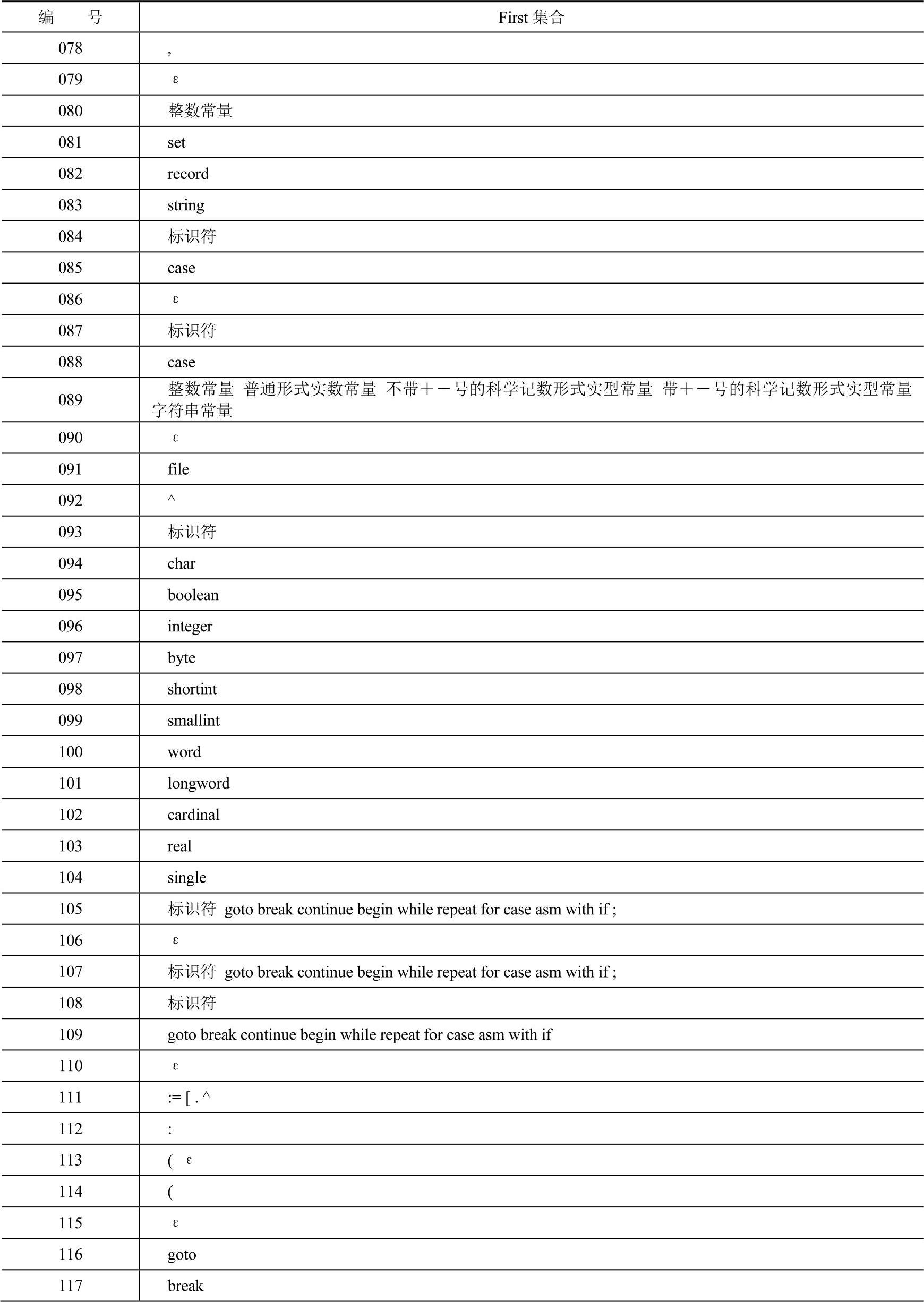
（续）

（续）

表3-4的编号列与表3—3中Neo Pascal文法的编号是对应的，即为产生式的编号。而表中First集合列则表示对应产生式的First集合。

Follow集合见表3-5。

表3-5 Neo Pascal文法的Follow集合

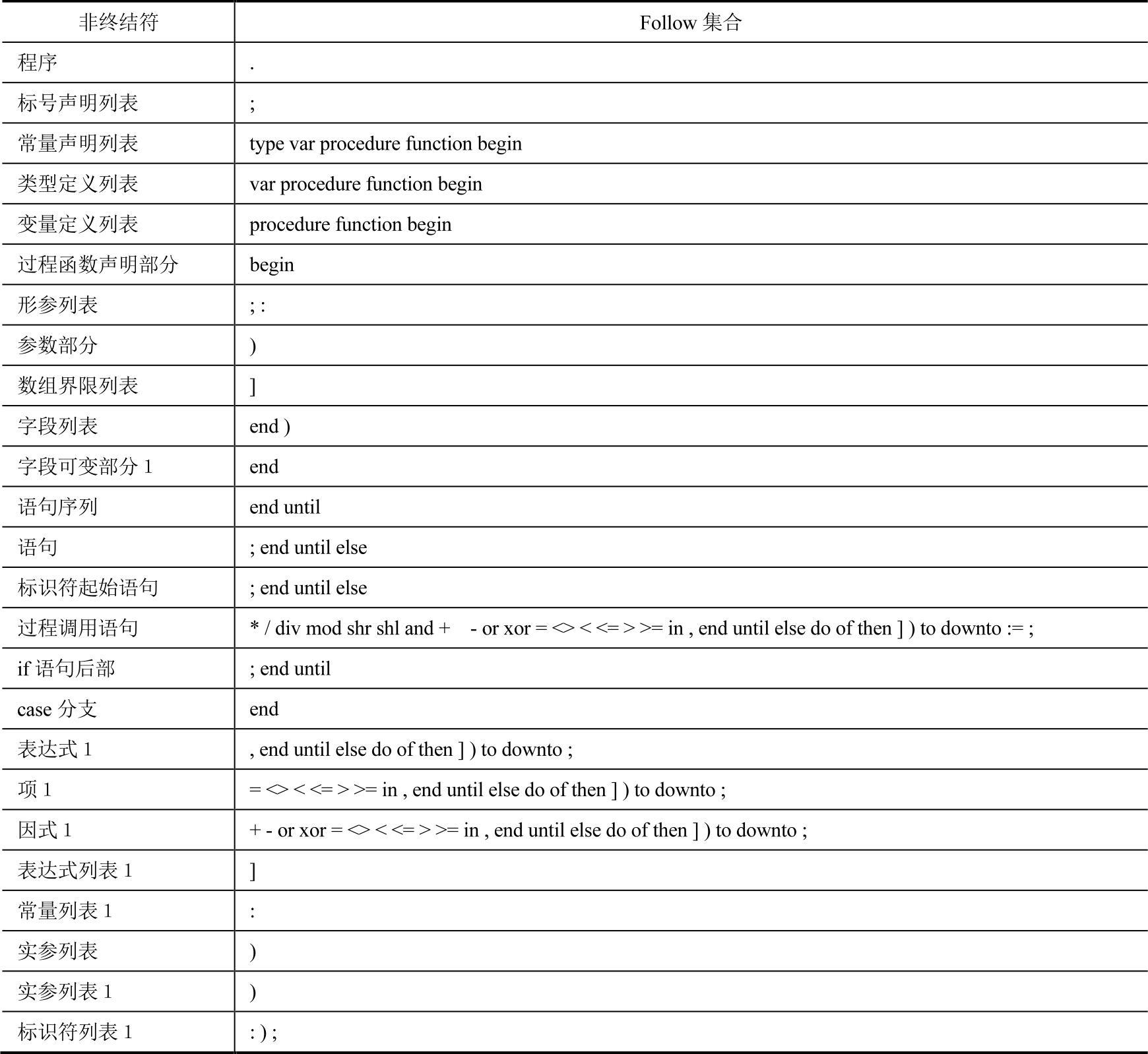
一个非终结符的Follow集合是唯一的，并且Follow集合仅在该非终结符存在空字候选式时才使用，故只需计算此类非终结符的Follow集合即可。

如果读者有手工构造Neo Pascal的Follow集合的经历，一定会发现Follow（if语句后部）={;end until else}与表3-5的Follow（if语句后部）={：end until}描述不尽相同。实际上，这并非计算错误。按照Follow集合的计算方法，Follow（if语句后部）={;end until else}是完全正确的。那么，到底是什么原因导致了两个不同的结果呢？这就是文法二义性造成的。文法的二义性在语法分析表构造时主要的表现就是冲突，即一个单元格中填入多个产生式的情况。如果Follow（if语句后部）=f：end until else}，则非终结符“if语句后部”的Follow集合与其相关First集合将存在交集，这将使语法分析表出现冲突。不过，值得注意的是，这并不意味着当一个单元格中填入了多个产生式时，就必定存在冲突。

实际上，这种现象并不罕见，例如，C、C++等同样存在类似的问题。在学习C语言时，读者应该记得C语言中else的就近匹配原则。如图3-7所示。

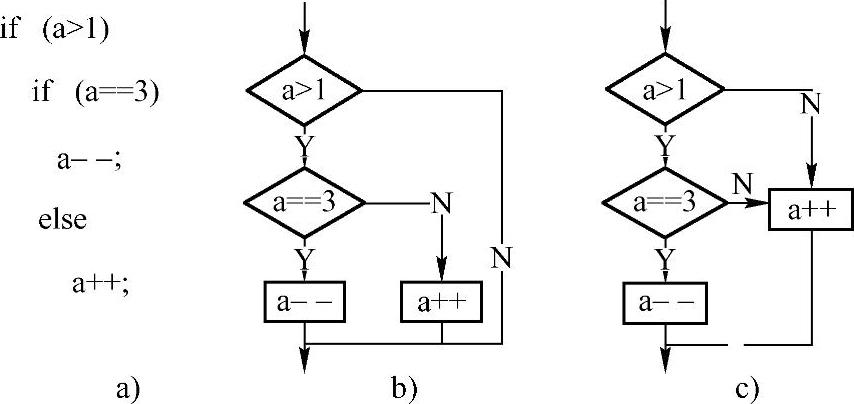
图3-7 if-else的流程示意图

a）代码 b）流程图1 c）流程图2

就程序的形式而言，以上两个流程图应该都是正确的，既可以将else与if（a>1）匹配，也可以将else与if（a==3）匹配。显然，从这两个流程图的分析，不同的匹配方式对程序流程及运行结果是完全不同的。换句话说，就意味着程序的语义是存在二义性的，这是程序设计语言不允许的。产生二义性的原因无非就是程序设计语言文法本身的原因。读者可以尝试编写一个类似上例的Pascal程序，然后，参考Neo Pascal文法推导验证此程序。不难发现，对于Neo Pascal的文法非终结符“if语句后部”遇到终结符“else”时，无论使用哪个候选式推导都是正确的。不过，生成的语法树是完全不同的，这就表明了二义性的存在。

那么，如何才能避免二义性呢？通常有两种解决方式，即修改文法或强制约定。(www.daowen.com)

（1）修改文法也就是通过改变if语句的结构来避免产生二义性。例如，BASIC就是通过在if语句结尾处增加endif关键字避免了产生二义性。

（2）强制约定也就是在各种语义中约定一种语义是正确的，将其他的语义排除。例如，C语言的else的就近匹配原则就是一种强制约定，它约定else只能匹配之前最近的一个if。根据这个原则，在上例中，else唯一能匹配的就是if（a==3）。这样，强制排除其他的语义，也就避免了二义性。

同样，Pascal语言也遵守else就近匹配原则，其约定与C语言完全一致。那么，这一约定如何在语法分析上体现呢？无非就是在非终结符“if语句后部”遇到终结符“else”时，确定选择一个候选式。这样，就能避免二义性了。那么，如何确定选择哪个候选式进行下一步推导才能满足else就近匹配原则呢？最简单的处理方法就是尝试用一个小例程推导一棵语法树，结果就非常明确了。答案就是当非终结符“if语句后部”遇到终结符“else”时，选择“if语句后部→else语句”这个候选式推导即可。由于没有选择使用ε产生式推导，因此必须将“else”从Follow（if语句后部）中剔除。

至此，if语句的二义性问题的就完美解决了。程序设计语言的二义性现象并不常见，类似if语句的二义性情况是非常特殊的。二义性既不利于语言的表述，也不利于编译器的设计。故在设计定义一门程序设计语言时，应该尽可能避免二义性。

计算得到了Neo Pascal的First集合与Follow集合后，就可以依此构造语法分析表了。这个工作并不复杂，先前，笔者也已经举例详述了其构造过程，故不再赘述。同时，囿于篇幅，笔者也不打算给出完整的语法分析表，读者可以参考本书的相关文档。

2.语法分析表的结构设计

顾名思义，语法分析表就是一张静态二维表，在编译器运行过程中仅作查询操作，其数据并不发生任何变化。显然，应用静态的二维数组存储语法分析表是比较理想的。由于C/C++的二维数组下标只能是整型，因此，有必要对文法的符号进行编码，即为每个文法符号分配一个唯一的编号(ID)。

文法的符号主要包括终结符、ε、非终结符。实际上，就LL(1)算法而言，不难发现，文法的终结符就是词法分析阶段的单词，因此，终结符的编号完全可以沿用词法分析中的单词ID，这是最简单且有效的方式。有关词法分析中的单词ID，读者可以参考表2-4。在表2-4中，将终结符编号归入了001~093之间。为了便于终结符的适当扩展，可以从100开始为非终结符编号，如表3-6所示。那么，剩下的只需编码为0即可。

表3-6 Neo Pascal文法非终结符表

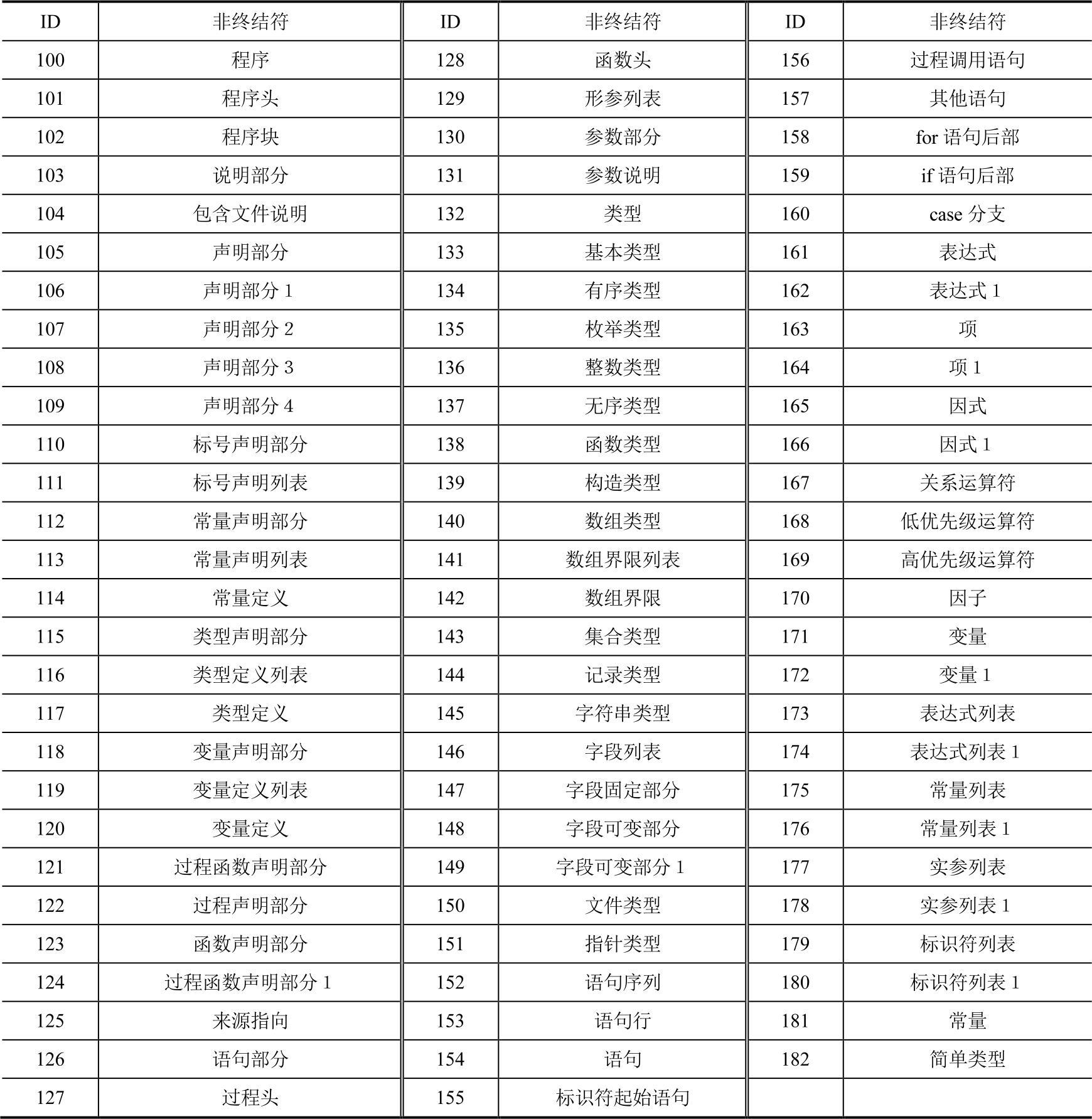
以上是标准文法的三类符号（非终结符、终结符、ε）的编码，这是构造与应用语法分析表的准备工作。

下面，着手处理语法分析表的表项设计。前面已经介绍过了，语法分析表的表项通常是文法产生式或出错标志（在Neo Pascal中记作“01”）。那么，应该如何设计语法分析表的表项结构呢？由于文法产生式是一串符号的集合，因此，将语法分析表的表项声明为字符串类型是可以接受的。不过，这种设计却给语法分析表带来了大量的冗余，字符串类型作为语法分析表的表项类型并不是非常合理的。那么，应当如何设计，使语法分析表的表项结构更为合理呢？通常设计一张单独表格来存储产生式及其编号，而在语法分析表的表项中只需存储产生式的编号或者出错标志即可，如图3-8所示。这样，就可以将语法分析表的表项声明为整型。与字符串类型的表项相比，整型表项的冗余度较小，占用的空间也较少。稍有数据库设计经验的读者不难想到这种设计方式与数据库设计的关系分解比较类似。关系分解是数据库原理课程的相关知识，读者可以参考相关书籍。第4章还会涉及一些数据库设计方面的理论。

图3-8是语法分析表的逻辑结构示意图，描述了检索语法分析表的过程。这里，以非终结符“语句”遇到终结符“标识符”为例说明。首先，以终结符的编号定位列，即图中终结符“标识符”的编号为001，故定位表格第1列。然后，以非终结符的编号定位行。由于非终结符的编号是从100开始的，但实际语法分析表没有必要从第100开始存储，因此，必须将非终结符的编号减去起始编号100后才进行行的定位。图中非终结符“语句”的编号为154，减去起始编号100为54，即定位到第54行。这样，语法分析器检索得到108，即表示选择编号为108的产生式进行下一步推导分析。这个检索过程并不复杂，读者结合图3-8应该可以理解。

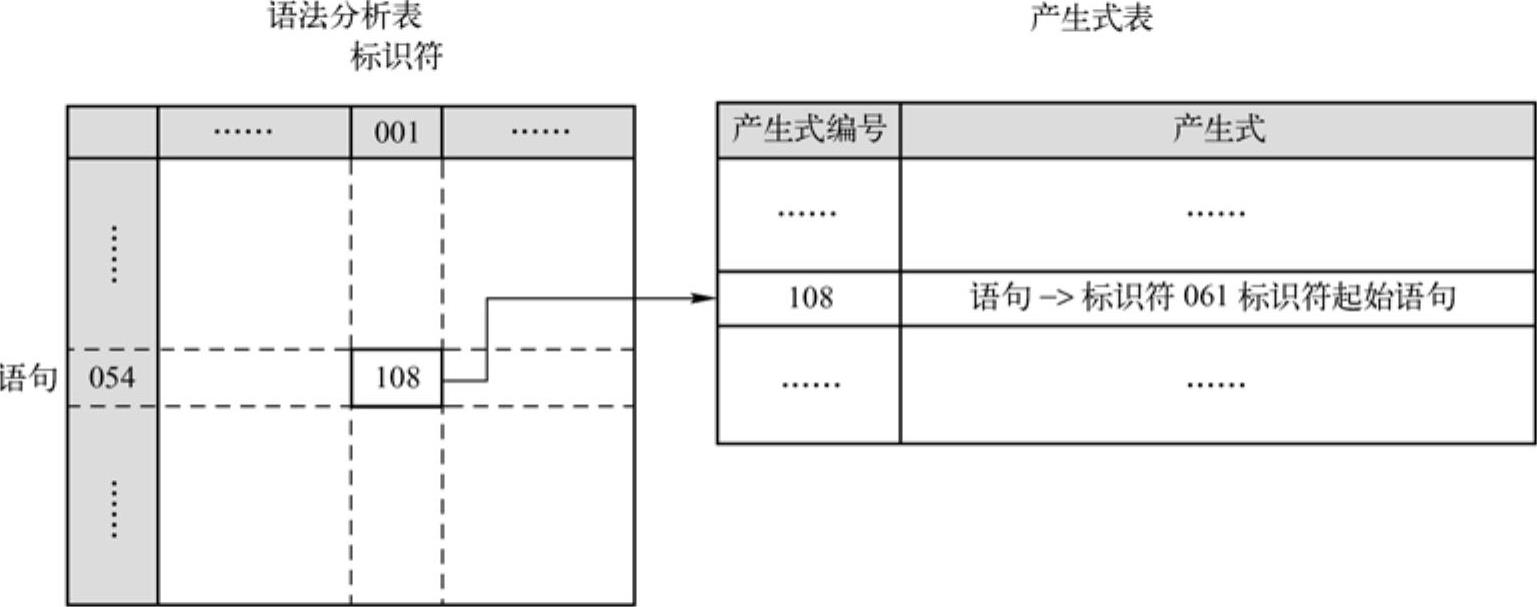
图3-8 语法分析表与产生式表的示意图

最后，再来讨论产生式表的存储形式。首先，读者仔细思考语法分析器选择候选式进行推导的过程。语法分析器先将栈项非终结符弹出，然后，将候选式的右部逆序入栈。整个推导过程始终只涉及候选式的右部，而没有使用候选式的左部。故方便起见，只需将产生式的右部存入产生式表即可。当然，产生式也同样需要编码。前面，已经给出了标准产生式右部的三类符号（终结符、非终结符、ε）的编码，这里，就可以直接运用了。然而，读者应该还记得Neo Pascal文法产生式中的那些奇怪数字。这里，笔者暂不解释这些数字的作用，只需将其加上300后编码即可。根据以上产生式编码的规则，图3-8中编号为108的产生式的编码为“001361155”。

综上所述，语法分析表是一个二维数组，数组元素的类型为整型。当元素值大于或等于0时，表示该元素值是产生式的编号（即产生式表的下标索引），否则表示该元素值是出错标志。产生式表是一个字符串列表，每个字符串表示一个产生式的编码序列。在产生式编码序列中，可以将三个ASCII字符作为一组，用于表示一个符号的编码。下面，笔者给出语法分析表、产生式表的结构声明：

【声明3-1l】

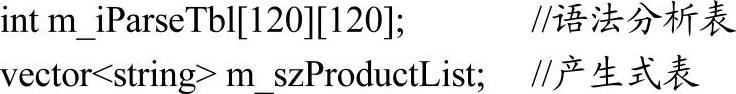
下面简单介绍一下Neo Pascal文法中的那些数字的作用。

前面提到过语法分析器并没有统一的输出形式，其中较为常见的输出形式是语法树。然而，至今所讨论的语法分析器似乎并没有考虑任何输出形式。构造的语法分析器也只是应用于验证输入源程序的语法正确性而已，显然，这与语法分析器的目标是不符的。而Neo Pascal中的数字正是实现语法分析器输出的重要元素一一语义子程序编号。

什么是语义子程序呢？顾名思义，就是完成语义分析处理的子程序。文法不同位置的语义几乎是完全不同的，例如，for语句的语义与if语句的语义是完全不同的。语义分析就必须根据不同的文法位置完成相应的分析工作。通常，根据语义分析的需求，在文法的适合位置插入相应的语义子程序，以实现语义分析的目的。在语法分析过程中，由语法分析器根据输入源程序调用相应的语义子程序，完成相应的语义分析工作。

那么，Neo Pascal文法中的数字正是语义子程序的编号。在此，读者不必深究语义分析的理论及语义子程序的实现，笔者将在第4～6章中详细讨论。只需理解文法中的数字是语义子程序的编号，将其看成产生式的一种特殊的符号即可。它与其他终结符或非终结符一样，在语法分析过程，同样需要压入分析栈。然而，当分析栈栈顶元素为语义子程序的编号时，语法分析器则将其出栈并调用相应的语义子程序，从而实现语义分析功能。

不难发现，在Neo Pascal文法中，语义子程序的编号与终结符的编号存在一定的冲突，即存在相同编号的现象。为了避免同号冲突，在构造语法分析表时，将语义子程序的编号加上300以避免冲突。而在语法分析过程中，当分析栈栈顶元素为语义子程序的编号时(即栈顶元素的值大于或等于300)，只需将此编号值减去300后调用相应的语义子程序即可。各类符号的编号范围如表3-7所示。

表3-7 各类符号的编号范围